Content

Intercepts and equations of lines

Intercepts

All lines, except those parallel to the \(x\)-axis or the \(y\)-axis, meet both coordinate axes. Suppose that a line \(l\) passes through \((a,0)\) and \((0,b)\). Then \(a\) is the \(x\)-intercept and \(b\) is the \(y\)-intercept of \(l\). The intercepts \(a\) and \(b\) can be positive, negative or zero. All lines through the origin have \(a=0\) and \(b=0\).

Set of axes with line l going through the points (0, b) and (a, 0).

Equations of lines

One of the axioms of Euclidean geometry is that two points determine a line. In other words, there is a unique line through any two fixed points. This idea translates to coordinate geometry and, as we shall see, all points on the line through two points satisfy an equation of the form \(ax+by+c=0\), with \(a\) and \(b\) not both 0. Conversely, any `linear equation' \(ax+by+c=0\) is the equation of a (straight) line. This is called the general form of the equation of a line.

Point–gradient form

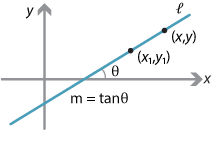
Consider the line \(l\) which passes through the point \((x_1,y_1)\) and has gradient \(m\).

Set of axes with line l at an angle of inclination of theta to the positive direction of the x axis. Points (x1, y1) and (x, y) on the line.
Detailed description

Let \(P(x,y)\) be any point on \(l\), except for \((x_1,y_1)\). Then

\[ m = \dfrac{y-y_1}{x-x_1}, \] and so \[ y-y_1 = m(x-x_1). \]

This equation is called the point–gradient form of the equation of the line \(l\).

Suppose that \((x_1,y_1)=(0,c)\). Then the equation is \(y-c=mx\) or, equivalently, \(y=mx+c\). This is often called the gradient–intercept form of the equation of the line.

Line through two points

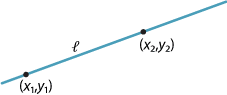
Line l with points (x1, y1) and (x2, y2) on the line.

To find the equation of the line through two given points \((x_1,y_1)\) and \((x_2,y_2)\), first find the gradient

\[ m=\dfrac{y_2-y_1}{x_2-x_1} \] and then use the point–gradient form \(y-y_1 = m(x-x_1)\).

A special case is the line through \((a,0)\) and \((0,b)\), where \(a,b \ne 0\).

Set of axes with line l going through the points (0, b) and (a, 0).

In this case, the gradient is

\[ m = \dfrac{b-0}{0-a} = -\dfrac{b}{a}. \]

Thus the equation of the line is

\begin{align*} y-0 &= -\dfrac{b}{a}(x-a)\\ ay+bx &= ab \end{align*} or, equivalently, \[ \dfrac{x}{a} + \dfrac{y}{b} = 1, \] which is easy to remember. This is called the intercept form of the equation of a line.
Summary

There are four different forms of the equation of a straight line which we have considered.

Equation of a straight line
General form \(ax+by+c = 0\)
Point–gradient form \(y-y_1 = m(x-x_1)\)
Gradient–intercept form \(y = mx+c\)
Intercept form \(\dfrac{x}{a}+\dfrac{y}{b} = 1\)


Example

  1. Find the equation of the line through \((3,4)\) with gradient 5.
  2. Find the equation of the line through \((3,4)\) and \((-2,-3)\).
  3. Find the equation of the line with \(x\)-intercept 3 and \(y\)-intercept \(-5\).

Solution

  1. The equation is \(y-4=5(x-3)\) or, alternatively, \(y=5x-11\).
  2. The gradient is
    \[ m = \dfrac{4-(-3)}{3-(-2)} = \dfrac{7}{5}. \]
  3. So the equation of the line is
    \[ y-4 = \dfrac{7}{5}(x-3) \]
    or, alternatively, \(7x-5y-1 = 0\).
  4. The equation is
    \[ \dfrac{x}{3}-\dfrac{y}{5} = 1 \]
    or, alternatively, \(5x -3y -15 = 0\).
Vertical and horizontal lines

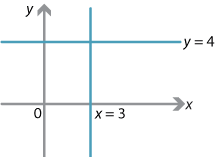
The equation of the vertical line through \((3,4)\) is \(x=3\). The equation of the horizontal line through \((3,4)\) is \(y=4\).

Set of axes with lines x = 3 drawn (parallel to y axis) and y = 4 (parallel to x axis).
Detailed description

Next page - Content - Parallel, intersecting and perpendicular lines