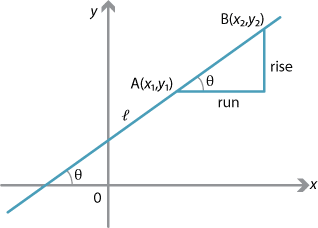Content

Gradients and the angle of inclination

Suppose \(l\) is a line in the number plane not parallel to the \(y\)-axis or the \(x\)-axis.

Set of axes with straight line l inclined at theta degrees to x axis.
Detailed description

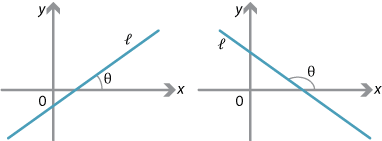
Let \(\theta\) be the angle between \(l\) and the positive \(x\)-axis, where \(0^\circ<\theta<90^\circ\) or \(90^\circ<\theta<180^\circ\). Suppose \(A(x_1,y_1)\) and \(B(x_2,y_2)\) are two points on \(l\). Then, by definition, the gradient of the interval \(AB\) is

\[ m = \dfrac{\text{rise}}{\text{run}} = \dfrac{y_2-y_1}{x_2-x_1}. \]

From the diagram above, this is equal to \(\tan\theta\). So \(\tan\theta\) is the gradient of the interval \(AB\). Thus the gradient of any interval on the line is constant. Thus we may sensibly define the gradient of \(l\) to be \(\tan\theta\).

Two sets of axes positive gradients
Detailed description

In the case where the line is parallel to the \(x\)-axis, we say that the gradient is 0. In the case where the line is parallel to the \(y\)-axis, we say that \(\theta=90^\circ\).

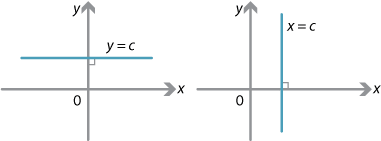
Two sets of axes.
\(\theta\) not defined no gradient \(\theta=90^\circ\)
Detailed description

Example

Find the gradients of the lines joining the following pairs of points. Also find the angle \(\theta\) between each line and the positive \(x\)-axis.

  1. \((2,3)\), \((5,3)\)
  2. \((1,2)\), \((7,8)\)
  3. \((1,2)\), \((7,-4)\)
  4. \((2,3)\), \((2,7)\)

Solution

  1. The line through \((2,3)\) and \((5,3)\) is parallel to the \(x\)-axis and so the gradient is 0.
  2. The gradient is \(\dfrac{8-2}{7-1} = 1\) and \(\theta = 45^\circ\).
  3. The gradient is \(\dfrac{-4-2}{7-1} = -1\) and \(\theta =135^\circ\).
  4. The line is parallel to the \(y\)-axis, so the line has no gradient and \(\theta=90^\circ\).

Exercise 5

Find the gradients of the lines joining the following pairs of points:

  1. \(\Bigl(cp,\dfrac{c}{p}\Bigr)\), \(\Bigl(cq,\dfrac{c}{q}\Bigr)\)
  2. \((ap^2,2ap)\), \((aq^2,2aq)\)
  3. \((a\cos\theta, b\sin\theta)\), \((a\cos\phi,b\sin\phi)\).

Next page - Content - Intercepts and equations of lines