Content

The distance between two points

Distances in geometry are always positive, except when the points coincide. The distance from \(A\) to \(B\) is the same as the distance from \(B\) to \(A\).

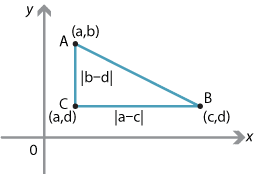
In order to derive the formula for the distance between two points in the plane, we consider two points \(A(a,b)\) and \(B(c,d)\). We can construct a right-angled triangle \(ABC\), as shown in the following diagram, where the point \(C\) has coordinates \((a,d)\).

Detailed description

Now, using Pythagoras' theorem, we have

\begin{align*} AB^2 & = |b-d|^2 + |a-c|^2\\ &=(a-c)^2+(b-d)^2. \end{align*}

So

\[ AB = \sqrt{(a-c)^2+(b-d)^2}. \]

A similar formula applies to three-dimensional space, as we shall discuss later in this module.

Interactive 1

The distance formula

Suppose \(P(x_1,y_1)\) and \(Q(x_2,y_2)\) are two points in the number plane. Then

\[ PQ^2 = (x_2-x_1)^2+(y_2-y_1)^2 \]

and so

\[ PQ = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2}. \]

It is clear from the distance formula that:

• \(PQ=QP\)
• \(PQ=0\) if and only if \(P=Q\).

Next page - Content - Midpoints and division of an interval