Content

The Cartesian plane

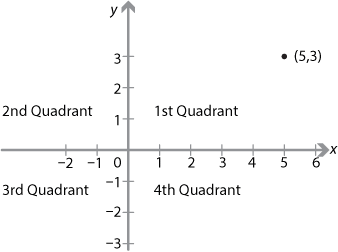
The number plane, or Cartesian plane, is divided into four quadrants by two perpendicular lines called the \(x\)-axis, a horizontal line, and the \(y\)-axis, a vertical line. These axes intersect at a point called the origin. Once a unit distance has been chosen, the position of any point in the plane can be uniquely represented by an ordered pair of numbers \((x,y)\). For the point \((5,3)\), for example, 5 is the \(x\)-coordinate and 3 is the \(y\)-coordinate, sometimes called the first and second coordinates. When developing trigonometry, the four quadrants are usually called the first, second, third and fourth quadrants as shown in the following diagram.

Detailed description

There are a number of elementary questions that can be asked about a pair of points \(A(a,b)\) and \(B(c,d)\).

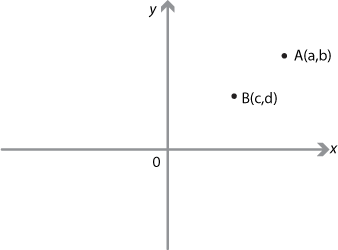
• What are the coordinates of the midpoint of the interval \(AB\)?
• What is the distance between the two points?
• What is the gradient of the interval joining the two points?
• What is the equation of the line joining the two points?

The answers to all of these questions will be discussed in this module, as will answers to other questions such as:

• What is the equation of the line through the origin parallel to \(AB\)?
• What is the equation of the perpendicular bisector of \(AB\)?
• At what angle does the line \(AB\) meet the \(x\)-axis?

These questions give some idea of the scope of coordinate geometry.

Next page - Content - The distance between two points