The Improving Mathematics Education in Schools (TIMES) Project
Experiences Before Starting School
Small children experience the language of time before they come to school. They will often be familiar with particular times of the day that relate to events in their lives such as bedtime or the start time of a favourite television program. They may be aware that clocks and watches are used to measure time.
Students in early primary school will develop understanding about time as they move through school.
By Year 4 it is expected that most students can:
- Use days of the week, months of the year, seasons and calendars.
- Tell time to the minute and use ‘past’, and ‘to’ for analogue and for digital clocks.
Measuring time and understanding about the duration of time are essential life skills.
The ability to understand how the days, weeks, months and years are structured,
how calendars work and the relationship of time to naturally occurring phenomena
helps us in our work and our leisure. Communicating with other people about time is extremely important.
Learning about time presents the child with some new concepts to understand. Students who have only recently learnt to count to a hundred have to cope with a complicated multibase system in which base 60, base 24 and base 7 all appear. In addition, they must be able to use both analogue and digital clocks. In learning about analogue clocks they will meet a mixture of markings and numbers around the face and the functions of the hour, minute and second hands must be understood. In addition, a considerable vocabulary including the names of the days and months has to be learnt.
Small children begin by comparing and ordering the duration of everyday events.
For example, eating an apple is quicker than driving from home to Grandmother’s
house.
Not all societies perceive time in the same way. Different cultures have used different calendars throughout history. For example, hours, days and weeks were introduced to some countries only with European settlement.
In temperate zones the seasons vary throughout the year. The seasons are marked by changes in the weather and the hours of daylight. These changes are caused by the tilt of the earth’s axis and the movement of the earth around the sun throughout the year.
The months of the year that fall in each season in Australia are conventionally:
| Spring − September, October, November Summer − December, January, February Autumn − March, April, May Winter − June, July, August |
In western cultures the seasons are usually spring, summer, autumn, and winter. In Old English, autumn used to be called fall because of the falling of the leaves from the trees, and this terminology is still used in some countries, including the USA. The term autumn comes from the Old French word autompne.
In tropical zones the seasons are quite different and some aboriginal tribes recognise six seasons.
Days and Years
There are two units of time that we can see, namely the day and the year.
One day is the time it takes the earth to make a full revolution on its own axis.
We can see days in the alternating pattern of days and nights.
One solar year is the time it takes the earth to make a full revolution as it orbits the sun. We can see years in the changing seasons. Each solar year is approximately 365 days long. Since a solar year is not a whole number of days, we use a calendar year to keep track of time. A calendar year has 365 days but we make up for the approximation by having 366 days in every fourth calendar year. We call a calendar year with 366 days in it a leap-year. This addition of one day every four years is in fact a slight overcompensation and we make up for this by skipping a leap-year every so often.
In terms of the Gregorian or standard calendar that is used in Australia, years that are divisible by 4 are leap years, unless they are divisible by 100, in which case they are not leap years. The exception is that years divisible by 400 are leap years. Thus 1600 and 2000 were leap years, whereas 1700, 1800 and 1900 were not. Looking to the future, 2100, 2200, 2300, 2500, 2600, 2700, 2900 and 3000 will not be leap years, but 2400 and 2800 will be.
Weeks and Months
In our calendar the twelve months and the number of days in each are as follows:
| January - 31 February − 28/29 March - 31 April - 30 May - 31 June - 30 |
July - 31 August - 31 September - 30 October - 31 November - 30 December - 31 |
The calendar months are loosely based on the movement of the moon. The origins of the word “month” are the same as those of the word “moon”. A lunar month is the time that it takes the moon to make a full revolution in its orbit around the earth. A lunar month is between 28 and 29 days long.
There are seven days in a week. This is possibly because there were approximately 28 days in a lunar month.
A rhyme that has been in use since the 15th century is one way to help remember the number of days in each month:
30 days hath September,
April, June and November,
All the rest have 31,
Except for February alone,
Which hath 28 days clear,
And 29 in each leap year.
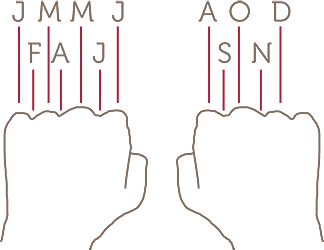
Another way to remember the number of days in a month is to count on the knuckles of one’s hand. Count the hills (knuckles) as months with 31 days, valleys between knuckles as those with 30 days, except for February.
The only way to learn to understand a calendar is to use one. Teachers of younger children include reading the calendar, naming the seasons, the month, the date and the day of the week as part of the daily classroom routine.
September, October, November and December get their names from the Latin prefixes sept-, oct-, nov- and dec- meaning seventh, eighth, ninth and tenth. This can be a little confusing because they are actually the ninth, tenth, eleventh and twelfth months in the calendar. January and February were originally the eleventh and twelfth months of the year respectively, but a decree by Julius Caesar changed the beginning of the year to January, changing the position of all other months by two.
In 46 BC, Julius Caesar reformed the Roman calendar to correct its astronomical alignment. It was decreed that each year was to consist of 365 days with a leap year in every fourth year, and the name of Caesar’s birth month, Quintilis, was changed to Julius. A short time after, Augustus further reformed the Roman calendar by correcting some confusion over the dates for leap years. The month Sextilis was renamed to Augustus in his honour.
CLASSROOM ACTIVITY
Use division to calculate how many weeks there are in a calendar year of 365 days.
(You will have a remainder.)
Hours, minutes and seconds
Each day is made up of smaller units of time.
| 1 day = 24 hours 1 hour = 60 minutes 1 minute = 60 seconds |
On the equator the 24 hours in the day are evenly split between day and night. So there are 12 hours of daylight and 12 hours of night every day on the equator.
CLASSROOM ACTIVITY
Why do clocks go clockwise? Make a sundial using paper (roll up a sheet of paper and cut one end at an angle to make the pointer stand at an angle). Use a torch to model the movement of the sun. In the northern hemisphere, the sun is to the south. How does the shadow of the pointer move as the sun moves from East to West?
If clocks had been invented in the southern hemisphere they would have gone anticlockwise!
Time is one of the few things that we measure using a system other than base ten. This is partly because the units of time that we can see such as days and years do not fit together in powers of ten.
It is also because the first clocks used over 3000 years ago were sundials. It was the Babylonians who decided there would be 360 degrees in a circle and 60 minutes in an hour. The Babylonians used a mixture of bases but mainly base 60.
The number 60 has twelve factors, namely 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 and 60 of which two, three, and five are prime numbers. One advantage of 60 is that one hour can be divided evenly into sections of 30 minutes, 20 minutes, 15 minutes, 12 minutes, 10 minutes, 6 minutes, 5 minutes, etc..
The way we measure time means that conversions between units of measure of time are more complicated than other measurement conversions.
To convert hours and minutes to minutes, multiply the number of hours by 60 to get minutes and add the extra minutes.
For example,
| 3 hours and 17 minutes | = 3 × 60 + 17 minutes |
|
| = 197 minutes |
Similarly when converting a time recorded in hours, minutes and seconds to seconds.
For example,
| 4 hours, 7 minutes and 23 seconds | = 4 × 60 × 60 + 7 × 60 + 23 | |
| = 14 400 + 420 + 23 | ||
| = 14 843 seconds |
To convert minutes to hours and minutes, count by multiples of 60 to get the number of hours and the remainder is the extra minutes. For example,
| 127 minutes | = 120 minutes + 7 minutes | |
| = 2 hours and 7 minutes |
If there are large numbers involved we divide by 60.
For example, to convert 4000 seconds to hours, minutes and seconds. First divide by
60 to get the number of minutes. The calculation is,
4000 ÷ 60 = 400 ÷ 6 = 66 |
and |  of 60 is 40. of 60 is 40. |
So, 4000 seconds = 66 minutes and 40 seconds.
Then divide by 60 again to get hours, minutes and seconds.
So, 4000 seconds = 66 minutes, 40 seconds = 1 hour, 6 minutes and 40 seconds
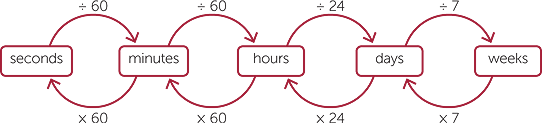
The following diagram illustrates these conversions.
EXAMPLE
Calculate the number of:
| a | seconds in 19 minutes | b | minutes in 16 hours | |||
| c | hours in 6 days | d | days and hours in 560 hours |
Solution
| a | 19 × 60 = 1140 seconds | (60 seconds in a minute) | ||
| b | 16 × 60 = 960 minutes | (60 minutes in an hour) | ||
| c | 6 × 24 = 144 hours | (24 hours in a day) | ||
| d | So 560 hours is 23 days and 8 hours. |
EXERCISE 1
- a
- How many seconds are there in 2 hours?
- b
- How many minutes have you been alive for?
Recording, reading and measuring time
Time can be described qualitatively, using words such as faster, slower, quicker, longer, and shorter. It can also be used quantitatively using units of measurement. Students need to learn both how to measure time and how to convert between units of time.
AM and PM
The word for midday in Latin is meridiem. We talk about hours before midday as being ante meridiem or am for short. We talk about hours after midday as being post meridiem or pm for short. So 7:00am means seven o’clock in the morning whereas 7:00pm means seven o’clock in the evening.
Traditionally the time 12am means midnight and 12pm means midday although it is best to avoid confusion by using the words midday and midnight instead.
Dates
We identify a day by giving its number, month and year. This is in accordance with the International Organization for Standardization standard ISO8601.
So the 8th of October 2025 would be 8-10-2025 or 8-10-25, although some people may write 8.10.25 or 8/10/25. In some countries, such as the USA, they write the month first followed by the day and then the year, writing 8th of October 2025 as 10-8-25.
To avoid confusion, many scientists, particularly astronomers, use a dating convention that starts with the largest unit and works towards the smallest; so they would write 2025-10-8. This notation is standard in China and is understood in all other countries. In this form the notation can be extended to include hours, minutes and seconds in the 24 hour clock, so that 45 seconds past 3:12pm on that day would be written 2025-10-8T15:12:45. The symbol T is used to indicate where the time measurement starts, in much the same way that we use a decimal point in Hindu-Arabic notation. The system can be extended to decimal fractions of a second for greater accuracy.
The abbreviations BC and AD are designations used to label the years before and after the birth of Jesus Christ. BC is the abbreviation for “Before Christ” and AD is the abbreviation for “Anno Domini”, the Latin for “in the year of Our Lord”. The designation of years as BC and AD did not begin until the sixth centruy when the abbot Dionysius Exiguus arranged the Christian calendar to identify the date of Easter. Usage of BC and AD was first adopted in Rome in the sixth century and throughout Europe in the eighth century. Under this system, it is not possible to have a year 0. The year before the birth of Christ is 1 BC and the year of his birth is designated as 1 AD, with no year in between.
Analogue clocks
 Analogue clocks consist of a circular face divided by markings into 60 arcs and two or three hands geared at the centre that rotate at a constant rate. Some analogue clocks have only the 12 numbers around the clock face, not all have 60 arcs.
Analogue clocks consist of a circular face divided by markings into 60 arcs and two or three hands geared at the centre that rotate at a constant rate. Some analogue clocks have only the 12 numbers around the clock face, not all have 60 arcs.
Students first need to understand that the different hands on the clock measure different things. It is hard to avoid phrases such as ‘the long hand’ and ‘the short hand’ or the ‘big hand’ and the ‘little hand’ because we have to explain which is the minute hand and which is the hour hand. However, it is important to gradually transition from physically descriptive terminology to the units of measurement.
Hour hand
A short thick hand is used to measure the hours. One full revolution of the hour hand on an analogue clock measures 12 hours of a day.
Minute hand
A longer and slightly thinner hand is used to measure minutes. The minute hand takes one hour to make a full revolution and each marking on the circle measures one minute.
Second hand
Some clocks have a long thin hand to measure seconds. The second hand takes one minute to make one full revolution with each marking on the circle measuring one second.
EXERCISE 2
- a
- How many degrees does each arc on the clock face represent? (That is, find the angle subtended by an arc at the centre)
- b
- How many minutes does each of the 60 arcs on the circle measure as the hour hand moves around?
The 24 hours in the day are divided into two pairs of 12 hours. The timing of sunset and sunrise varies over the year. Midday is when the sun is highest in the sky, though this will vary across a time zone. The clock hands all point straight up at midday.
The positions of the hour hand each hour are marked on the face of the clock with the numbers 1 to 12. Most analogue clocks are 12 hour clocks.
When children are learning to tell the time, parents and teachers usually start with times on the hour and introduce the word o’clock, which is a contraction of ‘of the clock’ or ‘on the clock’ and means according to the clock. Then the child can start to use half-hour times, and then should be encouraged to tell the time to five minutes and then to the minute.
Reading the time when the number of minutes is between 1 and 30 is done by saying the number of minutes past the hour. For example, 7:23 is read as ‘twenty-three minutes past seven’ and 7:11 is read as ‘eleven minutes past seven’.
Reading the time after half past the hour can be done in two ways. We can either read 7:35 as seven thirty-five or we can make an intermediate calculation that converts the number of minutes past the hour to the number of minutes ‘to’ the next hour.
We subtract the number of minutes from 60 minutes to get the number of minutes to the next hour. So, 7:35 is read as ‘twenty-five minutes to eight’ and 7:59 is read as ‘one minute to eight’.
We can also use fractions when we read the time. There are 30 minutes in half an hour and there are 15 minutes in a quarter of an hour. So, we read 7:30 as ‘half past seven’,
Digital clocks
On a digital clock the first two digits indicate the number of hours, and the next two digits indicate the number of minutes. So 06:23 is read as ‘six twenty-three’ or ‘twenty-three mintues past six’, and 11:48 is read as ‘eleven forty-eight’ or ‘twelve mintues to twelve’.

24-hour time
Digital clocks can display the time in traditional mode using am and pm but they sometimes use 24-hour time, particularly when there may be confusion if 12-hour time is used. Examples of this include airline schedules, in hospitals, in the armed forces or on the DVD player and oven at home. Twenty-four hour time means we start from 0000 at midnight and go all the way to 2359. The first two digits measure hours and the last two digits measure minutes. Often there is no colon used when writing 24-hour time.
If it is before midday then the 24-hour time is the same as with a twelve-hour clock.
So 0730 means 7:30am.
If it is after midday then the 24-hour time is 12 hours more than the time that would be shown on a 12-hour clock. For example, 1pm is really 12 + 1 hours, so 1:25pm is 1325
on a 24-hour clock. To go from 24-hour time back to analogue time we subtract 12 hours if necessary. So 0855 is still five to nine in the morning but 1645 is 4:45pm because
16 − 12 = 4.
 As the earth rotates, the part of the earth
facing the sun experiences day time and
the part facing away from the sun is
experiencing night.
As the earth rotates, the part of the earth
facing the sun experiences day time and
the part facing away from the sun is
experiencing night.
One way of demonstrating this to students is to use a torch and a globe of the world to discuss world time zones. Hold the torch in a fixed position so that it acts as the sun, then rotate the globe from west to east. Use the torch beam to show that when it is night in Europe, it is daytime here in Australia.
The world is divided into time zones. In a particular time zone the time is the same at all locations within it. Big countries like Australia and China have several time zones in them.
In Australia there are three time zones: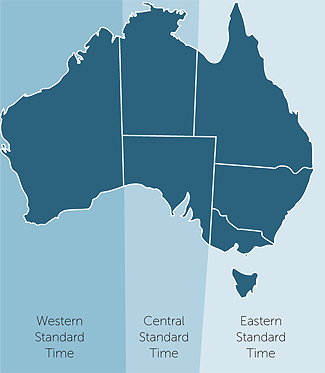
| EST = Eastern Standard Time |
| CST = Central Standard Time |
| WST = Western Standard Time |
| CST is EST minus 30 minutes, and WST is EST minus 2 hours. |
| There is an additional complication with summertime which varies from state to state and from year to year. |
Timelines can help us see how much time is spent on various things and they can assist in calculating elapsed time. School children are accustomed to mapping out a timeline representing their school day.
For example, Adrian gets up at 6am every morning and goes to bed at 9pm. Here is a timeline representing a typical weekday.

Timelines can also be used to describe events which take place over a long time.
Timeline of time measurement technology. [Source Wikipedia]
- 1600 BC Water clocks first used
- 270 BC - Ctesibius builds a popular water clock, called a clepsydra
- 46 BC - Julius Caesar and Sosigenes develop a solar calendar with leap years
- 11th century - Sets of hourglasses were maintained by ship's pages to mark the progress of a ship during its voyage
- 11th century - Large town clocks were used in Europe to display local time, maintained by hand
- 1335 - First known mechanical clock
- 1502 - Peter Henlein builds the first pocketwatch
- 1582 - Pope Gregory XIII, Aloysius Lilius, and Christopher Clavius introduce the Gregorian calendar with an improved leap year system
- 1655 - Cassini builds the heliometer of San Petronio in Bologna, to standardise Solar noon.
- 1656 - Christian Huygens builds the first accurate pendulum clock
- 1676 - Motion works and minute hand introduced by Daniel Quare
- 1680 - Second hand introduced
- 1737 - John Harrison presents the first stable marine chronometer, thereby allowing for precise longitude determination while at sea
- 1884 - International Meridian Conference adopts Greenwich Mean Time for consistency with Nevil Maskelyne's 18th century observations for the Method of Lunar Distances
- 1928 - Joseph Horton and Warren Morrison build the first quartz crystal oscillator clock
- 1946 - Felix Bloch and Edward Purcell develop nuclear magnetic resonance
- 1949 - Harold Lyons develops an atomic clock based on the quantum mechanical vibrations of the ammonia molecule
- 1982 - The Federation of the Swiss Watch Industry FH is founded by the merger of two previous organizations
- 1983 - Radio-controlled clocks become common-place
A timetable is a plan of times at which events are scheduled to take place.
EXAMPLE
This is a Year 5/6 timetable.
- a
- How much time is spent in class each day?
- b
- How much time is spent doing maths each week?
| Time | Monday | Tuesday | Wednesday | Thursday | Friday |
| 9:00−10:00 | English | English | Maths | English | Maths |
| 10:00−11:00 | English | English | English | English | English |
| 11:00−11:20 | RECESS | ||||
| 11:20−12:30 | Society | Maths | English | Music | Library |
| 12:30−13:30 | LUNCH | ||||
| 13:30−14:30 | Music | PE | Art | Maths | Science |
| 14:30−15:15 | Maths | Health | Art | Italian | PE |
Solution
| a | 1 hour + 1 hour + 1 hour 10 minutes + 1 hour + 45 minutes = 4 hours + 55 minutes | |||
| b | Monday | 14:30−15.15 = 45 minutes | ||
| Tuesday | 11:20−12:30 = 70 minutes | |||
| Wednesday | 9:00−10:00 = 1 hour | |||
| Thursday | 13:30−14:30 = 1 hour | |||
| Friday | 9:00−10:00 = 1 hour | |||
| Total | 3 hours 115 minutes which is 4 hours 55 minutes | |||
Sometimes we need to calculate how long it is between two times. This is called calculating elapsed time. The word ‘elapsed’ means ‘gone by’, so elapsed time means the amount of time that has gone by, or passed.
We calculate elapsed time by building up to whole minutes, hours or days, keeping track of the amounts of time as we go. For example, if Helen’s train left Maryborough at 2:55 pm and arrived at Daisy Hill at 3:45 pm, how long did it take? We can work out the elapsed time by building up from 2:55 to 3:00. Then there are 45 minutes more. Helen’s train trip took 50 minutes.
EXAMPLE
Marathon runners take around 3 hours to run 42km. If a runner started at 11:23:00 am (23 minutes past 11, no seconds) and finishes at 2:40:49 pm, what was the time taken to complete the marathon?
Solution
The time taken to complete the marathon is calculated by building up to the next whole minute or hour.
| time | hours | minutes | seconds | |
| Start time | 11:23:00 | |||
| Build up to | 12:00:00 | 37 minutes | ||
| Build up to | 2:00:00 | 2 hours | ||
| Build up to finish time | 2:40:49 | 40 minutes | 49 seconds | |
| Total | 2 hours | 77 minutes | 49 seconds | |
| Total time taken to complete the marathon (convert minutes to hours and minutes |
3 hours | 17 minutes | 49 seconds | |
Coordinated Universal Time (UTC) is the standard time common to every place in the world. It replaced Greenwhich Mean Time (GMT) as the World standard for time in 1986 and is based on atomic measurements rather than the rotation of the earth. Minor adjustments, called leap seconds, are sometimes made to allow for variations in the solar cycle. Coordinated Universal Time (UTC) is expressed using a 24 hour clock and is used in plane and ship navigation.
Links Forward AND APPLICATIONS
By the end of Year 8 students should be able to calculate elapsed time, convert between units of time and use timetables. Time is used in many other areas of mathematics. Secondary students will calculate speed and acceleration and it is common to construct graphs using time as one of the variables. They should be fluent with the use of both analogue and digital clocks.
The widespread use of mechanical clocks and watches to measure time is a relatively recent phenomenon and is closely linked to the industrial revolution. Factories necessitated large numbers of people working to fixed timetables. Getting to work on time was a major challenge for the majority of the workforce and many cities placed large clocks in strategic places to help keep workers to time. The Great Clock of Westminster, commonly known as Big Ben, is perhaps the most famous of these; it is the clock in the Palace of Westminster (the British Houses of Parliament in London) and first ticked on 31 May 1859.
The earliest clocks were sundials, but they were not useful at night! Early attempts to measure time without using sunlight included calibrated candles, hour-glasses with sand in them and water clocks that used flowing water to measure the passage of time. Waterclocks were used in ancient Egypt from the 16th century BC. By improving on the basic design, Ctesibius designed a particularly accurate water-clock in about 270 BC called a clepsydra. The clepsydra was so accurate that it outperformed the early mechanical clocks, and its accuracy was unmatched until the invention of the pendulum clock in the 18th century AD.
The measurement of time has always been essential for accurate navigation. When out of sight of land, navigation relies on accurate measurements of position in terms of latitude and longitude. Latitude (north-south distance from the equator) can be reasonably calculated from the angle of elevation of the sun at midday. East-west distance, which we now call longitude, is much more challenging to measure. One way to measure this, suggested by Hipparchus in the 2nd century BC, is to keep track of time at your point of origin. When it is midday at sea (when the sun is at its highest) you check the time at your point of origin and use the difference to calculate your east-west displacement.
Inaccurate time-keeping leads to getting lost and has been the cause of the loss of many lives at sea. Even when water clocks were available, hour- glasses with sand were used to keep time at sea because of the difficulty of running a clepsydra on a ship. The invention of pendulum clocks did not improve matters because the rocking of a ship significantly affects its accuracy. The problem was so significant that the British government established the Longitude Prize in 1714 as an incentive for increasing the accuracy of longitude calculations. The prize was finally awarded to John Harrison, the inventor of the marine chronometer, and most of the prize-money was paid to him in two instalments in 1765 and 1773.
Mechanical clocks using wheels were used by the Romans, and weight-driven clocks were in use in Italy in the 9th century. The oldest description of a mechanical clock dates
to 1379, written by Heinrich De Vick about the clock in the tower of the palace of Charles V of France. Galileo and Huygens worked on pendulum clocks in the 1600s.
The word calendar comes from the Latin kalendarium which was a list of payments that were due on the first days of the months, the kalendae. Calendars and the cycles of the moon were used by the early Christian Church to calculate the dates of Easter and other holy days. Ancient Chinese calendars changed with each Emperor, and were in use before 2000 BC.
History of Mathematics Volume II, D. E. Smith, Dover publications New York, (1953)
https://en.wikipedia.org/wiki/Timeline_of_time_measurement_technology
https://en.wikipedia.org/wiki/water_clock
EXERCISE 1
a) 2 x 60 x 60 = 7200 seconds.
b) answers will vary
EXERCISE 2
a) 360 ÷ 60 = 6°
b) 60 ÷ 5 = 12 minutes.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()


