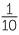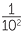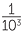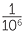The Improving Mathematics Education in Schools (TIMES) Project
Introduction to Measurement
Measurement and Geometry : Module 10![]() Years : 7-8
Years : 7-8
June 2011
- Some familiarity with the metric system.
- Informal idea of area from counting squares.
- Area of a rectangle and square.
- Time measurement - minutes, hours, days and weeks.
When building a table, putting a picture on the wall, taking some cough mixture, timing a race, and so on, we need to be able to make measurements. Measurement answers questions such as: how big, how long, how deep, how heavy? We buy material by the metre, and drive a number of kilometres. We state the floor space of a building in square metres, measure medicine in cubic centimetres, and buy milk by the litre. To pave a garden we need to know the area of the space to be paved and when filling a pool, we need to know the volume of water required. Thus measuring and calculating areas and volumes are two of the most basic mathematical skills needed in everyday life.
Accurate measurement is central in engineering, physics and and all branches of science. For example, astronomers need to measure time with extremely high accuracy since astronomical information is recorded from various parts of the earth and the information needs to be superimposed to obtain a complete picture. Scientific theory always requires experiment and testing and this often involves making very careful measurements, often at very small or very large orders of magnitude.
Consequently much effort is put into carefully defining what the basic unit of measurement should be.
In Australia and in most parts of the world, the metric system of measurement is used, with the basic units of length, mass and time being the metre (m), the kilogram (kg) and the second (s), respectively. The first two of these units are decimal, that is, they are based on multiples of 10. It is not convenient to measure time in a decimal system, both for historical and scientific reasons. For historical reasons a sexagesimal (base 60) system is used for time. Since we do not generally want to measure very large or very small distances in metres, (for example we would not measure the volume of a swimming pool in cubic centimetres), we need names for both larger and smaller units. We obtain convenient units linguistically by the use of prefixes and mathematically by multiplying or dividing by powers of 10. Thus kilo denotes 1000, centi denotes  and milli denotes
and milli denotes  .
.
|
Units of length |
|
|
10 millimetres (mm) |
= 1 centimetre (cm) |
|
100 centimetres (cm) |
= 1 metre (m) |
|
1000 millimetres (mm) |
= 1 metre (m) |
|
1000 metres (m) |
= 1 kilometre (km) |
|
Units of mass |
|
|
1000 milligrams (mg) |
= 1 gram (g) |
|
1000 grams (g) |
= 1 kilogram (kg) |
|
1000 kilograms (kg) |
= 1 tonne (t) |
|
Units of time |
|
|
60 seconds (s) |
= 1 minute (min) |
|
60 minutes (min) |
= 1 hour (h) |
|
24 hours (h) |
= 1 day (d) |
|
7 days |
= 1 week |
|
Units of fluid volume |
|
|
1000 millilitres (mL) |
= 1 litre (L) |
|
1000 litres (L) |
= 1 kilolitre (kL) |
In addition to these basic prefixes other measurement prefixes are also in common use.
Here is a list of some of the more commonly occurring ones.
|
Multiplying Factor |
Prefix |
Symbol |
|
one million = 106 |
mega- |
M |
|
one thousand = 103 |
kilo- |
k |
|
one tenth = |
deci- |
d |
|
one hundredth = |
centi- |
c |
|
one thousandth = |
milli- |
m |
|
one millionth = |
micro- |
µ |
There are prefixes to help name the very small and the very large. Nowadays we frequently hear of gigabyte, terabytes and nanotechnology. The prefix giga denotes 109, the prefix nano, 10-9, tera, 1012 and pico, 10-12.
EXERCISE 1
How many millilitres are there in an Olympic size pool, which holds 2.5 ML of water?
The perimeter of a polygon is the length of its boundary and is found by finding the sum of the lengths of its sides. We usually reserve the word circumference for the distance around a circle.
The area of a rectangle is the size of the region inside it and is obtained by multiplying
the lengths of its sides. For example, a 3 m by 4 m rectangle contains 3 × 4 = 12 squares, each with area 1 square metre. Thus the area of the rectangle is 12 square metres, or 12 m2.

We often label the sides of a rectangle as the length (l) and the width (w) and so we can write the formula for the area of a rectangle as A = l × w or simply A = lw.
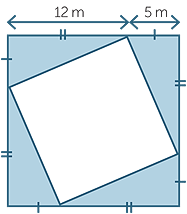
This formula makes sense if we have a rectangle whose sides are whole numbers. How do we deal with a rectangle with sides say, 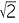 by
by 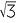 ? In this case we cannot divide the rectangle into unit squares (or even rational multiples of unit squares). Since the formula
? In this case we cannot divide the rectangle into unit squares (or even rational multiples of unit squares). Since the formula
A = lw works for rectangles whose sides are whole numbers, we take it as the definition
of the area of a rectangle with length l and width w.
We can then find the areas of composite figures by addition or subtraction.
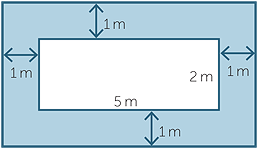
Example
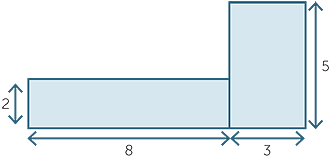 Find the area of the shaded region
Find the area of the shaded region
Solution
| Area | = 8 × 2 + 3 × 5 |
| = 16 + 15 | |
| = 31 | |
We can also find areas by subtracting a smaller area from a larger one.
Example
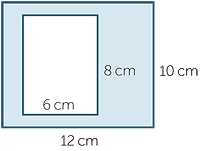 Find the area of the following shaded region.
Find the area of the following shaded region.
Solution
| Area | = 12 × 10 − 8 × 6 |
| = 120 − 48 | |
| = 72 cm2 | |
EXERCISE 2
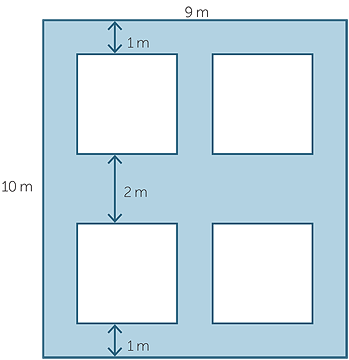 Calculate the area of the shaded region. Each small square has side length 3 m.
Calculate the area of the shaded region. Each small square has side length 3 m.
Every acute-angled triangle can be placed in a rectangle whose length is the same as the base of the triangle and whose width is the same as the height of the triangle.
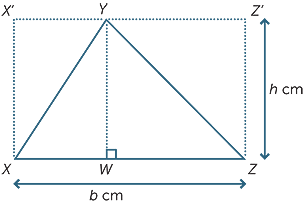
This diagram shows that the area of triangle XWY is half the area of the rectangle XWYX![]() ’ and that the area of triangle WZY is half the area of the rectangle WZZ
’ and that the area of triangle WZY is half the area of the rectangle WZZ![]() ’Y and so the area
’Y and so the area
of triangle XYZ is half the area of the rectangle XZZ![]() ’X
’X![]() ’.
’.
Thus, the area of the triangle with base b =XZ and height h =WY is given by half the area of the surmounting rectangle, so the area is half the base times the perpendicular height, or, written as a formula,
A =  h b
h b
What happens if the triangle is obtuse?

Take the obtuse-angle triangle ABC and extend BC to form, a right-angled triangle ADC.
The area of  ADC is
ADC is  × h × (x + b) =
× h × (x + b) =  × h × x +
× h × x +  × h × b.
× h × b.
Now subtract the area of  ADB, which is
ADB, which is  × h × x.
× h × x.
This gives area of  ABC =
ABC =  × h × b.
× h × b.
It may occur to a student to ask the question "When we turn the triangle around and thus choose a different height and base, how do we know that we will obtain the same value for  h b?" The following exercise shows that the quantity
h b?" The following exercise shows that the quantity  h b is the same in a given triangle for any of the three choices of base and height. The proof uses similar triangles.
h b is the same in a given triangle for any of the three choices of base and height. The proof uses similar triangles.
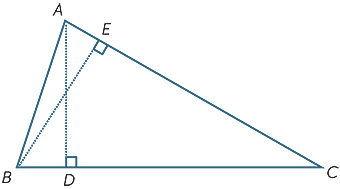
EXERCISE 3
In the diagram, triangle ABC has base length b and height h, or taking AC as the base, the base length is b1 and the height is h1.
- Explain why
 ADC is similar to
ADC is similar to  BEC.
BEC. - Deduce that hb = h1b1.
- Conclude that the quantity
 × base × height is the same for
either choice of base and height.
× base × height is the same for
either choice of base and height.
Alternative Approach
In the module, Area, Volume and Surface Area it will be shown how to use a simple dissection argument to prove that the area of a parallelogram with the base b and height h is equal to
h × b. This is summarised in the diagram below:
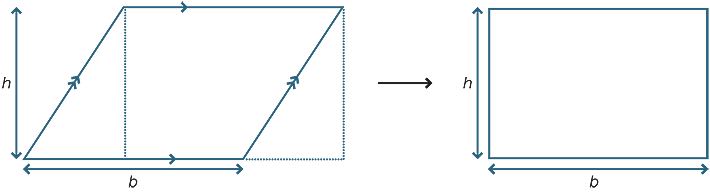
Area = hb
We can use this to find the area of a triangle. Starting with triangle ABC, we take a second copy of the triangle, rotated around as shown and join the two along the longest side as shown in the diagram.
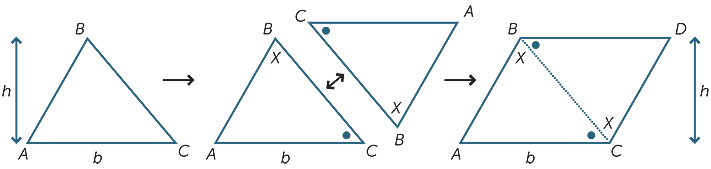
Since ![]() DBC =
DBC = ![]() ACB the lines BD and AC are parallel. Similarly,
ACB the lines BD and AC are parallel. Similarly, ![]() ABC =
ABC = ![]() DCB and so AB and CD are parallel. Thus, ABDC is a parallelogram and so its area is the base times the height. Clearly the parallelogram has twice the area of the triangle and so the area of the triangle is
DCB and so AB and CD are parallel. Thus, ABDC is a parallelogram and so its area is the base times the height. Clearly the parallelogram has twice the area of the triangle and so the area of the triangle is
 ×base × height as we saw before.
×base × height as we saw before.
Note that this argument works regardless of whether the triangle has an obtuse angle or not.
EXERCISE 4
Find the area of the shaded region in each figure below by adding and subtracting the areas of squares, rectangles and triangles as necessary.
| a |
|
b |
|
A right rectangular prism is a solid in which
- the base is a rectangle
- its horizontal plane cross-sections are rectangles congruent to the base
- all six faces are rectangles
(We usually leave out the word right which simply indicates that the ‘walls are vertical’)
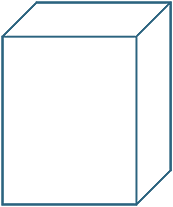
If all the faces of the prism are squares then the rectangular prism is a cube.
The volume of a rectangular prism is a measure of the space inside the prism.

Suppose the side lengths of the prism are 5 m, 4 m and 3 m as in the diagram.
We can cut the rectangular prism up into 1 cubic metre cubes. Altogether there are
5 × 4 × 3 = 60 cubes. We define the volume of each cube to be 1 cubic metre and then the volume of the rectangular prism is 60 cubic metres, or 60 m3. The side lengths of the rectangular prism are generally called the length, the width and the height and so the volume of a rectangular prism is given by:
| Volume of a rectangular prism | = length × width × height |
| = lwh |
As we did for area, since this formula makes sense when we have length, width and height that are whole numbers, we take it as our definition of volume when the measurements are not whole numbers.
You will notice that the volume is obtained by multiplying the area of the rectangular base by the perpendicular height. This is an important idea that will be revisited in the module, Area, Volume and Surface Area.
EXERCISE 5
A tank in the form of a rectangular prism has base dimensions 2.3 m by 1.4 m and holds water to a depth of 2 m. If the depth is increased by 3 m, what is the increase in the volume of water?
Scientists can measure very large and very small distances and there is a range of prefixes used for this purpose. For example, a nanometre is 10-9 metres or one billionth of a metre. The prefix nano- has given rise to the term nanotechnology which deals with constructing machines at almost molecular level. The prefix giga- denotes 109 times the basic unit. Thus, dam capacity is often given in gigalitres.
Using the basic ideas of the area of a rectangle and triangle, we can find formulas for the area of any polygonal figure which has sufficient rigidity for the area to be uniquely defined. (Note, for example, that the area of a quadrilateral cannot, in general, be determined if we only know the four sides.) Thus, we can find formulas for the area of a parallelogram, a rhombus, a kite and a trapezium.
Since a polygon is by definition a simple closed loop consisting of intervals joined end-to-end, circles are not polygons. However, circles can be approximated to an arbitrary degree of accuracy by polygons simply by increasing the number of sides. A similarity argument proves that the circumference of every circle is a constant multiple of its diameter independently of its actual size. We call this constant π, pronounced pi, which is approximately 3.1415926…. The circumference, C, of a circle is thus given by C = 2πr, where r is the radius of the circle. It can then be shown, by a limiting argument that the area A is given by A = πr2.
A right prism is a polyhedron (many faces) with two congruent parallel faces and all its remaining faces rectangles. A prism has a uniform cross section − in the case of a rectangular prism, the cross section is a rectangle. The volume of any right prism is defined to be the area of the cross section multiplied by the height. This idea can be extended to find the volume of a cylinder, since its base is a circle. The Greek mathematician Archimedes was able to find the volume (and surface area) of a sphere, again using the number π. The volume (V) is given by
V = 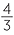 πr3.
πr3.
As well as a volume, a prism has a surface area, which is simply the total area of all the faces bounding the prism. Using our formulas for area, we can calculate the surface area of a prism and this notion can be extended to include cylinders and spheres.
In senior mathematics, integral calculus is used to find and give meaning to the area under a curve − an idea fundamental in physics − with many applications in engineering and elsewhere.
The need to measure goes back into antiquity. The Babylonians, and more particularly the Egyptians, found need to measure distances and area, the latter since the annual inundation by the Nile removed boundary markers, making land division impossible without some predetermined method of area measurement. While it is not possible to determine the area of a general quadrilateral knowing only the four sides, the Egyptians estimated the area of a quadrilateral with one pair of opposite side lengths a and b, and the other opposite side lengths c and d to be  (a + c)(b + d). You can use the sine rule to show that this gives a maximum value for the area of such a quadrilateral.
(a + c)(b + d). You can use the sine rule to show that this gives a maximum value for the area of such a quadrilateral.
Early units of measure related a given length to some part of the body − thus a cubit was the distance from the elbow to the tip of the longest finger and the inch was originally the length of the top joint of the thumb. Since these (and other such measures) vary from person to person, they were generally quite inaccurate. Standard measures, usually in the form of rods, were kept by the priests in temples and brought out when needed. Weight was measured using grains of wheat, while a lump of metal − whose weight in grains was known − would serve as the standard for a larger unit. Volume was a much more difficult quantity to measure, so weight probably would have played a greater role in antiquity than volume.
Time was also important to measure since it told people when to sow their fields and aided in the recording of events. Months − derived from observations of the moon − were probably mankind’s first attempt to measure time beyond the obvious day and night. The Babylonians knew roughly the length of the year since they divided the circle into 360 degrees probably because there were approximately that many days in the year. In ancient and medieval culture, the time from sunrise to sunset was divided into 12 parts − these ‘hours’ of course varied in length depending on the time of the year. The measurement of time using instruments such as sun dials and the Greek klepshydra or water clock led to more accurate measure of the hours of the day, although for the most part one simply talked about the number of hours after day break or before sunset. In the 14th century AD we begin to see the development of more accurate clocks − crucial for navigation − and the introduction of minutes and seconds, taken from the Latin terms: pars minuta prima (the first small part) and pars minuta secunda (the second small part).
The decimal metric system was created by the French in 1799 and standards for the metre and kilogram were set. This system was strongly promoted by the great mathematician Gauss, in Germany in 1832. Although the British introduced a system based on the centimetre, gram and second in 1874, which was used for scientific experimentation, they retained, for everyday use, the so-called Imperial System with its feet, inches, miles, furlongs etc and conversion factors such as 5280 feet to a mile, and 22 yards to a chain. Australia inherited this system at the time of European settlement. After further refinements and the addition of new units, in 1939 an international system was adopted based on the metre, kilogram, ampere and second to which were added the ampere, Kelvin and the candela as base units for temperature and luminosity, respectively. In 1960 this system was named the International System of Units, abbreviated to SI units. Finally in 1971 the mole was added bringing the total number of basic units to seven. Between 1960 and 1988 Australia adopted the SI units. In 1970 the Australian parliament passed the metric conversion act, and the Australian building trades made it the standard in 1974. (Note that to avoid confusion builders do not use centimetres, but rather record lengths in millimetres or in metres.)
Physicists, who often need extremely accurate measurements, have very carefully defined standards against which they can check their measuring instruments. Thus, in 1983, the metre was defined to be the distance travelled by light in a vacuum during a time interval of 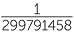 of a second.
of a second.
Units such as the angstrom, which is 10-10 metres, or the light year, which is 9.4605284 × 1015 metres, while frequently used by scientists, are not formally part of the SI systems of measurement.
A History of Mathematics: An Introduction, 3rd Edition, Victor J. Katz, Addison-Wesley, (2008)
History of Mathematics, D. E. Smith, Dover publications New York, (1958)
www.measurement.gov.au/measurementsystem/Pages/HistoryofMeasurementinAustralia.aspx
EXERCISE 1
2 500 000 000 millilitres = 2.5 × 109 millilitres
EXERCISE 2
54 m2
EXERCISE 3
a![]()
![]() ADC =
ADC = ![]() BEC = 90o
BEC = 90o
![]()
![]() ECB =
ECB = ![]() DCA
DCA
![]()
 ADC is similar to
ADC is similar to  BEC (AA)
BEC (AA)
b ![]() BC = b, AD = h, AC = h1, BE = b1
BC = b, AD = h, AC = h1, BE = b1
![]()
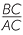 =
= 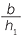 and
and 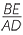 =
= 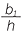
![]() Therefore,
Therefore, 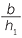 =
= 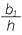
![]() bh = h1b1
bh = h1b1
c![]() Area =
Area =  bh =
bh =  h1b1
h1b1
EXERCISE 4
a ![]() 120 m2
120 m2
b ![]() 18 m2
18 m2
EXERCISE 5
9.66 m3
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()