The Improving Mathematics Education in Schools (TIMES) Project
- Familiarity with fractions and decimals.
- Facility with basic algebra including algebraic fractions
- Familiarity with the difference of two squares and simple binomial expansions.
- Familiarity with Pythagoras’ theorem.
When applying Pythagoras’ theorem, irrational numbers such as  naturally arise. When solving a quadratic equation, using either the method of completing the square or the quadratic formula, we obtain answers such as
naturally arise. When solving a quadratic equation, using either the method of completing the square or the quadratic formula, we obtain answers such as 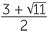 ,
, 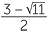 . These numbers involve surds. Since these numbers are irrational, we cannot express them in exact form using decimals or fractions. In some problems we may wish to approximate them using decimals, but for the most part, we prefer to leave them in exact form. Thus we need to be able to manipulate these types of numbers and simplify combinations of them which arise in the course of solving a problem. There are a number of reasons for doing this:
. These numbers involve surds. Since these numbers are irrational, we cannot express them in exact form using decimals or fractions. In some problems we may wish to approximate them using decimals, but for the most part, we prefer to leave them in exact form. Thus we need to be able to manipulate these types of numbers and simplify combinations of them which arise in the course of solving a problem. There are a number of reasons for doing this:
- approximating irrationals by decimals when problem solving can lead to rounding error. Thus it is best, if possible, to approximate at the end of a calculation and work with exact values at each step. As soon as we approximate, information is lost.
- working with exact values enables us to see important simplifications and gives further insight that would be lost if we approximate everything using decimals.
- surds give the students further practice with algebraic ideas and reinforce their basic algebra. Just as we can only combine like terms in algebra, so we can only combine like surds.
- several of the trigonometric ratios of 30°, 45° and 60° (as well as other angles) turn out to be expressible in terms of surds. Again, it is best to leave the answers in exact surd form rather than approximate. It is a lovely result in trigonometry that cos 72° =
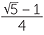 . This is much more remarkable and gives us much better insight than simply writing
. This is much more remarkable and gives us much better insight than simply writing
cos 72° ≈ 0.30902, (correct to 5 decimal places)! - the technique of rationalising the denominator, which is developed to handle surds in the denominator, arises in other settings in algebra, calculus and later mathematics. A similar technique, is needed when dealing with quotients of complex numbers.
For all these reasons, an ability to manipulate and work with surds is very important for any student who intends to study mathematics at the senior level in a calculus-based or statistics course.
The number 9 has two square roots, 3 and −3. However, when we write 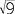 we always mean the positive square root, 3 and not the negative square root −3, which can be written as −
we always mean the positive square root, 3 and not the negative square root −3, which can be written as −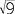 . Every positive number has exactly two square roots. The expression
. Every positive number has exactly two square roots. The expression 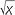 is only defined when x is positive or zero. For cube roots, the problem does not arise, since every number has exactly one cube root. Thus
is only defined when x is positive or zero. For cube roots, the problem does not arise, since every number has exactly one cube root. Thus 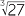 = 3 and
= 3 and  = −2. Further detail on taking roots is discussed in the module, Indices and logarithms.
= −2. Further detail on taking roots is discussed in the module, Indices and logarithms.
If a is a rational number, and n is a positive integer, any irrational number of the form  will be referred to as a surd. A real number such as 2
will be referred to as a surd. A real number such as 2 will be loosely referred to as a surd, since it can be expressed as
will be loosely referred to as a surd, since it can be expressed as 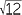 . For the most part, we will only consider quadratic surds,
. For the most part, we will only consider quadratic surds,  , that involve square roots. We will also say that
, that involve square roots. We will also say that  +
+  is a surd, although technically we should say that it is the sum of two surds.
is a surd, although technically we should say that it is the sum of two surds.
If a, b are positive numbers, the basic rules for square roots are:
- (
 )2 = a
)2 = a  = a
= a ×
× 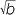 =
= 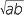
 ÷
÷ 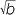 =
=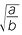 .
.
The first two of these remind us that, for positive numbers, squaring and taking a square root are inverse processes.
Note that these rules only work when a, b are positive numbers. Note that in general
 ≠ a. Thus, the oft quoted ‘conundrum’ 1 =
≠ a. Thus, the oft quoted ‘conundrum’ 1 = 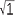 =
=  =
= 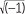 ×
×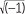 = −1 has its first error in the third equal sign. Also the
= −1 has its first error in the third equal sign. Also the 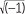 is not defined.
is not defined.
Note also that the number π is not a surd. It cannot be expressed as the nth root of a rational number, or a finite combination of such numbers. Indeed, π is a transcendental number - see the module, The Real Numbers.
As in algebra, we write 2 for 2 ×
for 2 ×  .
.
In order to manipulate surds properly, we need to be able to express them in their simplest form. By simplest form, we mean that the number under the square root sign
has no square factors (except of course 1). For example, the surd  can be simplified
can be simplified
by writing
 =
=  =
=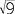 ×
×  = 3
= 3 .
.
In the second step, we used the third rule listed above. Simplifying surds enables us to identify like surds easily. (See following page for discussion of like surds.)
EXAMPLE
Simplify 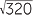 .
.
Solution
Take out any obvious square factors
|
|
= |
|
= 8 |
Repeat the process if possible.
Thus, 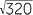 = 8
= 8 .
.
EXERCISE 1
Simplify  .
.
In order to compare the size of two or more surds, we may need to reverse the process and express a surd in the form n rather than the form bn
rather than the form bn .
.
EXAMPLE
Write the following from smallest to largest.
3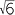 , 2
, 2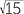 , 4
, 4
Solution
3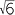 =
=  , 2
, 2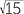 =
=  , 4
, 4 =
= 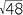 , hence
, hence
4 < 3
< 3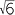 < 2
< 2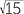 .
.
Addition and subtraction of surds
There is no simple way to express the sum  +
+  in simpler form. These two surds are called unlike surds, in much the same way we call 2x and 3y unlike terms in algebra. On the other hand 5
in simpler form. These two surds are called unlike surds, in much the same way we call 2x and 3y unlike terms in algebra. On the other hand 5 and 3
and 3 are like surds. We can simplify the sum 5
are like surds. We can simplify the sum 5 + 3
+ 3 to 8
to 8 , since we can simply think of it as
, since we can simply think of it as
‘5 lots of  plus 3 lots of
plus 3 lots of  equals 8 lots of
equals 8 lots of  .
.
Thus, we can only simplify the sum or difference of like surds.
When dealing with expressions involving surds, it may happen that we are dealing with surds that are unlike, but which can be simplified to produce like surds. Thus, we should simplify the surds first and then look for like surds.
EXAMPLE
Simplify 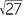 + 2
+ 2 +
+ 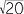 − 2
− 2 .
.
Solution
Simplifying first, we obtain
|
|
= 3 |
|
= |
This expression cannot be simplified further.
EXERCISE 2
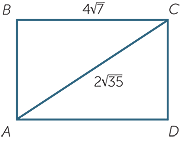 In the diagram, find BA and the perimeter of the rectangle in surd form.
In the diagram, find BA and the perimeter of the rectangle in surd form.
Multiplication and division of surds
When we come to multiply two surds, we simply multiply the numbers outside the square root sign together, and similarly, multiply the numbers under the square root sign, and simplify the result. A similar procedure holds for division.
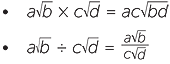
EXAMPLE
|
Find |
a |
4 |
b |
15 |
|||||
|
Solution |
|||||||||
| a |
4 |
= 8 |
b |
15 |
|||||
|
= 16 |
The Distributive Law and Special Products
The usual rules of algebra also, hold when pronumerals are replaced by surds.
For example the identities,
a(b + c) = ab + ac, (a + b)(c + d) = ac + ad + bc + bd are useful.
After expanding, it will often be necessary to simplify the surds as well.
EXAMPLE
Expand and simplify
a![]() 2
2 (4 + 3
(4 + 3 )
) ![]() b
b![]() (3
(3 − 4
− 4 )(5
)(5 −
−  )
)
Solution
|
a |
||
|
b |
(3 |
= 15 |
|
= 19 |
||
A very important special identity is the difference of squares.
![]() (a − b)(a + b) = a2 − b2
(a − b)(a + b) = a2 − b2
EXAMPLE
Expand and simplify (2 − 3
− 3 )(2
)(2 + 3
+ 3 ).
).
Solution
(2 − 3
− 3 )(2
)(2 + 3
+ 3 ) = (2
) = (2 )2 − (3
)2 − (3 )2 = 20 − 18 = 2.
)2 = 20 − 18 = 2.
Notice in the above example, since we are taking a difference of squares, the answer turns out to be an integer. We will exploit this idea in the next section.
EXERCISE 3
Caculate (5 + 7
+ 7 )(5
)(5 − 7
− 7 ).
).
In addition to the important difference of two squares mentioned above, we also have the algebraic identities:
![]() (a + b)2 = a2 + 2ab + b2
(a + b)2 = a2 + 2ab + b2![]() and
and![]() (a − b)2 = a2 − 2ab + b2,
(a − b)2 = a2 − 2ab + b2,
![]() that also, of course, apply to surds.
that also, of course, apply to surds.
EXAMPLE
Expand and simplify
a![]() (5
(5 + 3
+ 3 )2
)2 ![]() b
b![]() (3
(3 −
− 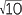 )2
)2
Solution
a![]() (5
(5 + 3
+ 3 )2 = 25
)2 = 25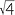 + 9
+ 9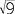 + 30
+ 30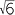 = 77 + 30
= 77 + 30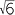 .
.
b![]() (3
(3 −
− 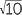 )2 =9
)2 =9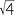 + 10 − 6
+ 10 − 6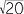 = 28 − 12
= 28 − 12 .
.
EXERCISE 4
Suppose x and y are positive number, show that 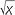 ×
×  =
= 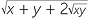 and hence
and hence
simplify 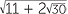 .
.
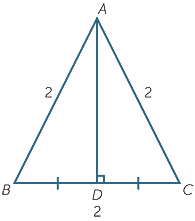
EXERCISE 5
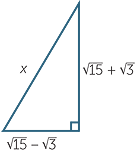 Find the area and perimeter of the following triangle.
Find the area and perimeter of the following triangle.
In the pre-calculator days, finding an approximation for a number such as 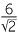 was difficult to perform by hand because it involved calculating
was difficult to perform by hand because it involved calculating 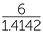 (approximately) by long division.
(approximately) by long division.
To overcome this, we multiply the numerator and denominator by  to obtain
to obtain
![]()
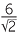 ×
× 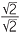 =
= 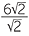 = 3
= 3 .
.
We can then approximate and write
![]()
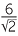 = 3
= 3 ≈ 3 × 1.4142 = 4.2426, to four decimal places.
≈ 3 × 1.4142 = 4.2426, to four decimal places.
Since the introduction of calculators, this is no longer necessary.
There are many occasions in which it is much more convenient to have the surds in the numerator rather than the denominator. This will be used widely in algebra and later in calculus problems.
The technique of removing surds from the denominator is traditionally called rationalising the denominator (although in practice we make the denominator a whole number).
EXAMPLE
Rationalise the denominator of 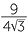 .
.
Solution
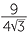 ×
× 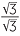 =
= 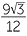 =
= 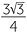 .
.
Binomial denominators and conjugate surds
In the expression  , it is not obvious to remove the surds from the denominator.
, it is not obvious to remove the surds from the denominator.
To do this, we exploit the difference of two squares identity, (a + b)(a − b) = a2 − b2.
If we multiply  +
+  by
by  −
−  we obtain 7 − 5 = 2.
we obtain 7 − 5 = 2.
The numbers  +
+  and
and  −
−  are said to be conjugates of each other.
are said to be conjugates of each other.
2 + 7 and 2 − 7
and 2 − 7 are also said to be conjugate to each other.
are also said to be conjugate to each other.
Thus, the method we will employ to rationalise the denominator involving such surds, is to multiply the top and bottom by the conjugate of the surd in the denominator.
EXAMPLE
Express the following surds with a rational denominator.
a![]()
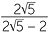
![]() b
b![]()
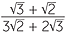
Solution
a![]()
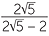 =
= 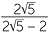 ×
× 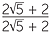 =
= 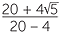 =
= 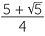 .
.
b![]()
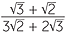 =
= 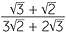 ×
× 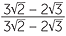 =
= 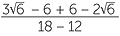 =
= 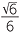 .
.
This last example shows quite dramatically how rationalising denominators can, in some cases, simplify a complicated expression to something simpler. However if all that is wanted is an approximation a calculator could be used.
All of the ideas discussed above can be discussed for surds of the form  .
.
For example:
- 5
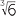 + 7
+ 7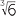 = 12
= 12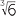
- 2
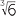 × 4
× 4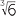 = 8
= 8
 ×
×  = 10
= 10
Surds arise naturally when solving quadratic and some higher order equations. If we begin with a quadratic that has integer coefficients and solutions which are surds, then it can be shown that the surds are conjugates of each other. Thus, for example, if we know that a certain quadratic equation with integer coefficients has 2 +  as one of its solutions, then we can say that the other solution is 2 −
as one of its solutions, then we can say that the other solution is 2 − .
.
Indeed, we can go further and find the monic quadratic equation that has these surds as solutions.
Factor the monic quadratic x2 + bx + c as (x − α)(x − β).
Expanding this and comparing coefficients gives α + β = −b, αβ = c.
Hence, taking α = 2 + , β = 2 −
, β = 2 −  , we have
, we have
![]() b = −4, c = (2 +
b = −4, c = (2 +  )(2 −
)(2 − ) = −3
) = −3
and so the monic quadratic equation with roots 2 +  , 2 −
, 2 −  is
is
![]() x2 − 4x − 3 = 0.
x2 − 4x − 3 = 0.
 Apart from solving quadratics, surds also arise in trigonometry.
Apart from solving quadratics, surds also arise in trigonometry.
The angles 30°, 45°, 60° have the following trigonometric ratios.
Triangle ABC is equilateral. AD is the line interval from A to the midpoint of BD. Triangles ABD and ACD are congruent (SSS).
 ABD =60°,
ABD =60°,  BAD = 30° and Pythagoras’ theorem gives
BAD = 30° and Pythagoras’ theorem gives
that AD =  .
.
Hence,
sin 30° = cos 60° = 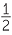 , , |
sin 60° = cos 30° = 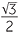 , , |
||
tan 30° =  and and |
tan 60° =  . . |
Using a square divided by a diagonal we form two isosceles right-angled triangles and can see sin 45° = cos 45° =  and tan 45° = 1.
and tan 45° = 1.
The technique of rationalising the denominator can also be applied in algebra.
EXAMPLE
Express 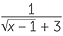 without the ‘surd’ in the denominator.
without the ‘surd’ in the denominator.
Solution
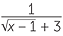 =
= 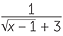 ×
× 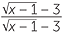 =
= 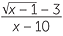 .
.
This technique is used in calculus when we wish to find the derivative y =  from first principles. In that case, we move the square root from the numerator to the denominator.
from first principles. In that case, we move the square root from the numerator to the denominator.
We may also need to do this to find certain limits as the following example shows.
EXAMPLE
Find 
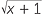 −
−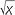 .
.
Solution
We cannot find this easily as it stands. We will shift the surds into the denominator by using the conjugate expression. This process is called rationalising the numerator.
 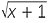 − − 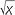 |
=  ( (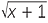 − − 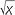 ) )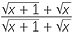 |
=  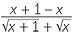 |
|
=  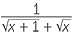 |
|
| = 0 |
EXERCISE 6
Find 
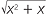 − x.
− x.
(After shifting the surds to the denominator, you will need to divide top and bottom carefully by x in order to find the limit. The answer to this problem is somewhat surprising! Try substituting some large values of x on your calculator to confirm your answer.)
We can extend the technique to deal with trinomial denominators such as 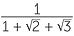 .
.
We firstly multiply top and bottom by ((1 +  ) −
) −  ). This will remove the term involving
). This will remove the term involving  , then continue the process as before.
, then continue the process as before.
EXERCISE 7
Complete the problem as outlined above.
A complex number is number of the form a + ib where a, b are real numbers and the number i has the property that i2 = −1.
Given an number such as 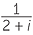 we seek to express it in the form a + ib. Thus we need to shift the number i to the top. This is done by realising the denominator, which is achieved in a similar way to rationalising the denominator. The conjugate of 2 + i is 2 − i.
we seek to express it in the form a + ib. Thus we need to shift the number i to the top. This is done by realising the denominator, which is achieved in a similar way to rationalising the denominator. The conjugate of 2 + i is 2 − i.
Thus we write,
![]()
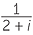 =
= 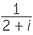 ×
× 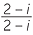 =
= 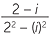 =
= 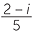 =
= 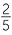 −
− 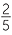 i.
i.
The integers are contained within the set of rational numbers and likewise, the rational numbers are contained within the set of real numbers. Mathematicians study sets of numbers that lie `between’ the integers and the real numbers.
For example, we can form the set Z[ ] = {a + b
] = {a + b : a, b integers}. This set behaves in many ways like the integers − we can add, subtract and multiply and we stay within the set. We can also factorise numbers inside this set into other numbers also belonging to the set. Thus we can define analogues to the prime numbers within this set. The set contains the set of integers, (put b = 0), and is contained within the set of real numbers.
: a, b integers}. This set behaves in many ways like the integers − we can add, subtract and multiply and we stay within the set. We can also factorise numbers inside this set into other numbers also belonging to the set. Thus we can define analogues to the prime numbers within this set. The set contains the set of integers, (put b = 0), and is contained within the set of real numbers.
It is an example of a quadratic extension of the integers.
Similarly, we can form the set Q[ ] = {a + b
] = {a + b :a, b rationals}. This set behaves in many ways like the rationals − we can add, subtract, multiply and divide and obtain numbers still belonging to the set. This set contains all of the rational numbers and is a subset of the real numbers. It is an example of a quadratic number field. Sets such as these have assisted mathematicians in solving all sorts of problems in number theory, and motivate ideas to many branches of modern abstract algebra.
:a, b rationals}. This set behaves in many ways like the rationals − we can add, subtract, multiply and divide and obtain numbers still belonging to the set. This set contains all of the rational numbers and is a subset of the real numbers. It is an example of a quadratic number field. Sets such as these have assisted mathematicians in solving all sorts of problems in number theory, and motivate ideas to many branches of modern abstract algebra.
We have mentioned in several other modules (see especially the module on the Real numbers) that the Greeks discovered irrational numbers, in the form of surds, when applying Pythagoras’ theorem.
One of the best known surds from the Greek world is the so-called Golden Ratio
![]()
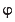 =
= 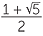 ≈ 1.618034.
≈ 1.618034.
This number arises geometrically from the following problem.
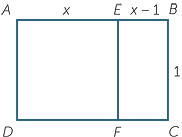
Consider the 1 × x rectangle ABCD as shown. The line EF cuts off a 1 × 1 square AEFD as shown. We seek to find the value of x such that the rectangle EBCF is similar to the original rectangle ABCD.
The Greeks believed that such a rectangle is aesthetically pleasing to the eye and indeed, the base rectangle of the Parthenon was built using a rectangle similar to to the one described above.
Since AEFD is a square, AD = AE = EF = DF = 1, FC = 1 − x. Also, since the rectangles are similar, 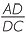 =
= 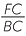 and so
and so  =
= 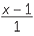 . Cross-multiplying and re-arranging, we arrive at the quadratic equation which we can solve using the quadratic formula to produce,
. Cross-multiplying and re-arranging, we arrive at the quadratic equation which we can solve using the quadratic formula to produce,
x = 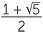 ,
, 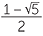 . Since x is positive, we take the solution x =
. Since x is positive, we take the solution x = 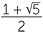 . Traditionally this number is given the symbol
. Traditionally this number is given the symbol 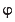 and it is called the golden ratio.
and it is called the golden ratio.
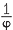
EXERCISE 8
Find the value of 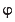 2 and
2 and 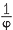 . Also prove that
. Also prove that 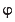 = 1 +
= 1 + 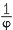 and
and 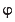 3 =
3 = 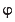 2 +
2 + 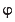 .
.
The golden ratio arises in many places in mathematics − most notably in its connection to the Fibonacci numbers. It also arise in various ratios of sides in the regular pentagon and pentagram. The latter has made it a favourite of those who look for mystical properties in numbers. The connection with the pentagon and pentagram is, however, hardly surprising, since 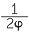 = cos 72° and this angle arises naturally in such figures.
= cos 72° and this angle arises naturally in such figures.
Bhaskara (1114-1185) was an Indian Mathematicians wrote two important works, the Lilavati (named after his daughter) which was concerned with arithmetic and the Vijaganita concerned with algebra. He was the first to handle the arithmetic of surds and gave the formula  +
+ 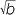 =
= 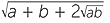 which was mentioned in an earlier exercise. In later Arabic mathematics we also see the more exotic rules such as
which was mentioned in an earlier exercise. In later Arabic mathematics we also see the more exotic rules such as
![]()
 +
+ 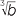 =
= 
Bhaskara often wrote mathematics in poems, for example:
The square root of half the number of bees in a swarm
Has flown out upon a jasmine bush
Eight ninths of the swarm has remained behind
A female bee flies about a male who is buzzing inside a lotus flower
In the night, allured by the flower’s sweet odour, he went inside it
And now is trapped!
Tell me, most enchanting lady, the number of bees.
This is equivalent to solving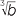 +
+ 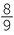 x + 2 = x, (which has solution x = 72).
x + 2 = x, (which has solution x = 72).
During the period known as the Dark Ages in the West, Greek mathematics was copied, polished and extended by Arabic mathematicians in the regions currently known as Iraq and Iran and also in Moslem Spain, especially in Granada. During this period little mathematics was done in the West, but the Arab mathematicians translated Greek mathematics into Arabic − some of it now lost in the Greek and only surviving in Arabic.
In the 12th century, when Granada fell back into the hands of the West, translators from Europe travelled to Spain and began translating the Arabic mathematical texts into Latin. Although good scholars, they were sometimes confused both by the Arabic and also by the mathematics when they were undertaking their translations. One such confusion led to the word surd coming into mathematical language. The word is a shortened form of surdus which is Latin for deaf. When the Arab mathematicians came upon the Greek word alogos − irrational, without reason, they translated it by the Arabic word asamm which means both irrational and deaf. Thus rational and irrational numbers were called audible and inaudible numbers respectively by Arabic mathematicians. The latter translators, not understanding the purpose of the word, translated asamm by surdus.
In the 15th century, when algebra was developing in the West, surds were written using an abbreviated notation. For example, Cardano (1501-1576) would have written 2 +  as 2pr2, where the p stands for plus and r for radix − Latin for root. It is believed that the modern square root sign developed from the letter r.
as 2pr2, where the p stands for plus and r for radix − Latin for root. It is believed that the modern square root sign developed from the letter r.
Cardano also worked with cube roots, since in his famous book the Ars Magna, (The Great Art), he gives a method for solving cubic equations. This method is outlined below, since it may be of interest to some teachers. It is not part of the high school curriculum.
The Solution of the Cubic
To solve x3 + 3x + 1 = 0, we put x = u + v. Substituting and moving the last two terms to the opposite side we have
![]() (u + v)3 = −1 − 3(u + v).
(u + v)3 = −1 − 3(u + v).
Now the left hand side can be expanded and then written as
![]() (u + v)3 = u3 + v3 + 3u2v + 3uv = u3 + v3 + 3uv(u + v).
(u + v)3 = u3 + v3 + 3u2v + 3uv = u3 + v3 + 3uv(u + v).
Hence, u3 + v3 + 3uv(u + v) = −1 − 3(u + v).
We now ‘equate’ u3 + v3 = − 1 and 3uv = −3. This last equation can be divided by 3 and then cubed to give u3v3 = −1. Thus we have the sum and product of the numbers u3, v3. We can therefore construct a quadratic equation with these number as its roots, since we have the sum and product of the roots. The quadratic is z2 + z − 1 = 0. We can solve this to obtain z =  ,
, 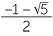 and these two numbers represent u3, v3 , in either order. Taking cube roots and adding, we obtain
and these two numbers represent u3, v3 , in either order. Taking cube roots and adding, we obtain
![]() x =
x = 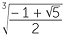 +
+ 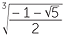 .
.
This method will always work for cubics which have only one real root. Strange things happen when we try to apply the method to cubics with three real roots.
EXERCISE 1
2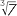
EXERCISE 2
BA = 2 , Perimeter = 12
, Perimeter = 12
EXERCISE 3
−23
EXERCISE 4
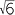 +
+ 
EXERCISE 5
Area = 6 and Perimeter = 2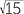 + 6
+ 6
EXERCISE 6
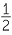
EXERCISE 7
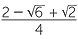
EXERCISE 8
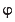 2 =
2 = 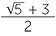 ,
,  =
= 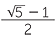
1 + 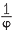 = 1 +
= 1 + 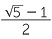 =
= 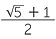
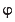 3 =
3 = 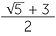 ×
× 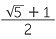 = 2 +
= 2 + 
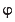 4 +
4 + 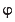 =
= 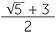 +
+ 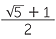 = 2 +
= 2 +  .
.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()


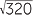 =
= 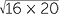

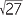 + 2
+ 2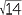 × 2
× 2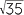 ÷ 5
÷ 5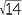 × 2
× 2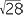
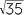 ÷ 5
÷ 5