The Improving Mathematics Education in Schools (TIMES) Project

return to index

The Integers

Number and Algebra : Module 15Years : 7-8

June 2011

PDF Version of module

Assumed knowledge

• Fluency with addition, subtraction, multiplication and division of whole numbers including:
• understanding that subtraction is the inverse operation of addition
  (The statement 32 + 54 = 86 is equivalent to the statement 86 − 54 = 32)
• understanding that division is the inverse operation of multiplication
  (The statement 6 × 4 = 24 is equivalent to the statement 24 ÷ 4 = 6)
• the use of the commutative, associative and distributive laws when calculating
• the role of 0 and 1.
• Using a number line for understanding and calculating with whole numbers including
• order
• addition and subtraction
• multiplication as repeated addition.

Motivation

Negative numbers appear in everyday experiences. For example, temperatures can take negative values and financial calculations often involve the use of negative numbers.

In these modules we use the term whole numbers for the numbers

0, 1, 2, 3,….

This name is used instead of the term natural numbers because of differing definitions of the natural numbers, which can either include or exclude the number 0. Other terms, which are used for these numbers, are ‘cardinal numbers’ and ‘counting numbers’.

The whole numbers are represented as points on the number line.

The point labelled 0 is the starting point for counting to the right. Every whole number can be reached in a finite number of unit steps to the right from 0.

Within the whole numbers we can calculate 7 − 4 and 4 − 4 to obtain whole numbers, but we cannot make sense of 4 − 7 as a whole number. We need to ‘extend’ the whole numbers to complete this calculation.

If we have $30 in a bank and we take $50 from an ATM the bank records the balance as −$20

Content

To make sense of a calculation such as 4 − 7 we can extend the number line to the left of zero in the same way as on the right with the whole numbers.

The whole numbers, together with these new numbers ….,−5, −4 ,−3, −2, −1 are called the integers. The integers consist of the numbers:

…, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5,…

The numbers 1, 2, 3, 4, 5,… are called the positive integers.

The numbers …,−5, −4, −3, −2, −1 are called the negative integers.

The number 0 is neither positive nor negative.

We want the integers to follow the usual rules for arithmetic that the whole numbers follow. For example, for whole numbers we have the ‘commutative rule for addition
a + b = b + a’ and we want this to be true if a and b are integers.

The number line

The integers are represented as points on the number line.

An integer a is defined to be less than another integer b if a lies to the left of b on the number line. The symbol < is used for ‘less than’. For example, −3 < 1, −5 < 2 and −6 < 0.

An integer b is greater than another integer a if b lies to the right of a on the number line. The symbol > is used for ‘greater than’. For example, 1 > −5.

Note that a < b if and only if b > a as shown in the diagram below

a < b and b > a

The opposite of an integer

The number −2 is called the number the opposite to 2. It is the same distance from 0,
but lies on the opposite side of 0.

• The opposite of 2 is −2 and the opposite of −2 is 2. The opposite of 0 is 0.
• We will write the opposite of the number a as −a.
• If a is a positive number −a is a negative number.
• If a is a negative number −a is a positive number.
• The opposite of 0 is 0. That is, −0 = 0.
• Notice that the opposite of the opposite of a number is the number we started with.

For example, −(−2) = 2 and −(−(−2))) = −2.

Adding and subtracting a positive integer

The number line provides a useful model for addition and subtraction of integers.

Adding a positive integer

When you add a positive integer, you move to the right along the number line.

For example, to calculate −3 + 4, start at −3 and move 4 steps to the right, so −3 + 4 = 1

Money also provides a useful model. For example: the statement −3 + 4 = 1 can be modelled as:

I had a debt of $3, but I earned $4. I now have $1.

Subtracting a positive integer

We will start by thinking of subtraction as ‘taking away’.

When you subtract a positive integer, move to the left along the number line.

For example, to calculate 2 − 5: start at 2 and move 5 steps to the left. We see that 2 − 5 = −3.

This subtraction can also be understood in terms of money.

I had $2 and I spent $5. I now have a debt of $3.

We can also think of subtracting as answering the question ‘What do I add on?’ but to do this we first have to look at how to add a negative number.

Adding a negative integer

Adding a negative integer to another integer means that you take a certain number of steps to the left on the number line.

The result of the addition 4 + (− 6) is the number you get by moving 6 steps to the left, beginning at 4.

4 + (−6) = −2

Notice that 4 − 6 is also equal to −2.

You can also start at a negative number. The result of the addition −2 + (− 3) is the number you get by moving 3 steps to the left, beginning at −2.

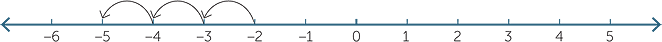
Notice that −2 − 3 is also equal to −5.

All additions of this form can be completed in a similar way. For example:

4 + (−7) = −3		and		4 − 7 = −3
−11 + (−3) = − 14		and		−11 − 3 = − 14

Notice that −11 − 3 = − (11 + 3).

This suggests the rule:

Subtracting a negative integer

We have already seen that adding −2 means taking 2 steps to the left.
For example, 7 +(−2) = 5.

We want subtracting −2 to be the reverse process of adding −2.

So to subtract −2, we will take two steps to the right. For example, 7 −(−2) =9.

There is a very simple way to state this rule:

We confirm this rule by considering subtraction as answering the question ‘What do I add on?’

To evaluate 2 − (−3) we ask the question ‘What do I add onto −3 to obtain 2?’

This gives the result 2 − (−3) = 5 and gives further evidence for the rule in the box above.

Addition and subtraction as translations

On the number line, 0 − 6 + 4 can be considered as a translation of 6 to the left from 0, followed by a translation of 4 to the right.

Also, 0 + 4 − 6 can be considered as a translation of 4 to the right from 0, followed by a translation of 6 to the left.

This reassures us that indeed −6 + 4 = 4 − 6 = −2, in agreement with commutative law for addition in the integers.

Subtraction defined as adding the opposite

We have added negative integers by considering the ‘opposite’ of a number.

For each number a there is a number −a (the opposite of a) that satisfies:

a + (−a) = 0.

For example 5 + (−5) = 0 and (−7) + (−(−7)) = 0

Note that we could have defined subtraction of integers by ‘a − b = a + (−b)’. This is quite a reasonable way to do subtractions. We write:

To subtract an integer add its opposite

With this approach:

3 − (−5) = 3 + (−(−5)) = 3 + 5 = 8

Multiplication

The product 5 × (−3) means 5 lots of −3 added together.

That is, 5 × (−3) = (−3) + (−3) + (−3) + (−3) + (−3) = −15.

We want multiplication of integers to satisfy the commutative law a × b = b × a. Just as 8 × 6 = 6 × 8 we will take (−3) × 5 to be the same as 5 × (−3). All products like this are treated in the same way.

For example:

(−6) × 3 = 3 × (−6) = −18.

The question remains of what multiplying two negative integers together means.

We have seen that −(−a) = a for any integer a. If a is a positive integer a × (−1) = −a.
We would like this to be true for all integers.

That is, we agree that

a × (−1) = −a = −1 × a for all integers.

For example, for a = −2, (−2) × (−1) = −(−2) = 2.

This allows us to multiply any negative integers together.
Two ways of doing this are shown here:

(−3) × (−5)	= (−1 × 3) × (−5)		(−3) × (−5)	= (3 × (−1))×(−5)
	= −1 × (3 × (−5))			= 3 × (−1 × (−5))
	= −1 × (−15)			= 3 × 5
	= 15			= 15

The careful reader will notice that we assumed both the commutative and associative rules for multiplication.

We can write the rule as:

A product of two negative integers is a positive integer.

The multiplication table below supports this result.

In the left−hand panel we list the multiples of 5. The products decrease by 5 each time.

In the right−hand panel we are taking multiples of −5. The products increase by 5 each time.

3 × 5 = 15	3 × (−5) = −15
2 × 5 = 10	2 × (−5) = −10
1 × 5 = 5	1 × (−5) = − 5
0 × 5 = 0	0 × (−5) = 0
−1 × 5 = −5	−1 × (−5) = 5
−2 × 5= −10	−2 × (−5) = 10
−3 × 5 = −15	−3 × (−5) = 15

 

We have the following rules.

Division

Every multiplication statement, for non−zero whole numbers, has an equivalent
division statement.

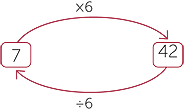
For example, 7 × 3 = 21 is equivalent to 21 ÷ 3 = 7 and 21 ÷ 7 = 3. We will use this to establish the rules for division involving the integers.

Here are some examples:

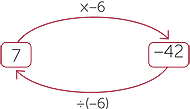
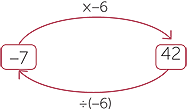
That is 7 × 6 = 42 is equivalent to 42 ÷ 6 = 7.		That is 7 × (−6) = −42 is equivalent to −42 ÷ (−6) = 7.
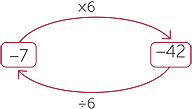
That is −7 × 6 = −42 is equivalent to −42 ÷ 6 = −7.		That is −7 × (−6) = 42 is equivalent to 42 ÷ (−6)= −7.

 

Indices and order of operations

• You need to be particularly careful with the order of operations when dealing with negative numbers.
  
  For example, −42 = −16 but (−4)2 = 16.
  
  To evaluate −42, first square 4 and then take the opposite, −42 = −(4 × 4) = −16.
  
  To find ( −4)2, square −4, ( −4)2 = −4 × (−4) = 16.
  
  Notice that the two answers are different.
  
  
• Remember that multiplication is done before addition. For example,
  
  (−3) × 5 + 2 = −15 + 2 = −13 and (−3) × (5 + 2) = (−3) × 7 = −21
  
  The same general rules as we had previously for whole numbers apply when
  dealing with negative numbers.

Strategies for integer arithmetic

Efficient calculations with the integers are made simpler through methods that are not necessarily included in the above discussion.

For example:

To calculate 45 × (−23) we complete the calculations as −(45 × 23) = −1035.

To calculate 459 ÷ (−9) we complete the calculation −(459 ÷ 9) = −51.

To calculate 564 − 700 we complete the calculation −(700 − 564) = −136.

The rearrangement of expressions often simplifies calculations. For example:

−234 + 800 is equal to 800 − 234.

Rearrangement can help in the evaluation of expressions as shown here:

13 − 17 + 25 − 20 = (13 + 25) − (17 + 20) = 1

Undertaking the operations from left to right can also be effective.

13 − 17 + 25 − 20 = −4 + 25 − 20 = 21 − 20 = 1

History

There is no evidence of the Greeks mentioning negative numbers. For example, the Greek mathematician Diophantus (275 AD) described the equation 4x + 20 = 4 as impossible.

Brahmagupta, an Indian Mathematician, wrote important works on mathematics and astronomy including a work called Brahmasphutasiddhanta (The Opening of the Universe) in the year 628. This book is believed to mark the first appearance of the rules for negative numbers in the way we know today. He gives the following rules for positive and negative numbers in terms of fortunes (positive numbers) and debts (negative numbers).

A debt subtracted from zero is a fortune.

A fortune subtracted from zero is a debt.

The product of zero multiplied by a debt or a fortune is zero.

The product of zero multiplied by zero is zero.

The product or quotient of two fortunes is a fortune.

The product or quotient of two debts is a fortune.

The product or quotient of a debt and a fortune is a debt.

The product or quotient of a fortune and a debt is a debt.

After Brahmagupta other Hindu writers used negative numbers and all Hindu mathematicians used the rules discussed by Brahmagupta from about 850AD.

In Europe, Fibonacci (1225) interpreted a negative solution of a linear equation in a financial problem as a loss instead of a gain but little else was done in medieval times in Europe.

The first of the 16th century writers to consider negative numbers was Cardano. In his book Ars Magna (1545) he found negative solutions of equations and gave a clear statement of the rules we have discussed in this chapter.

When negative numbers did begin to make an appearance different notations were used. For example, Bombelli (1572) writes m5 for −5, while in 1598 Tycho Brahe begins to use the minus sign. We do not know exactly when the − sign was first used.

The acceptance of negative numbers was established during the seventeenth century through the work of mathematicians such as Fermat and Descartes.

Appendix: Construction of the Integers

In this module we developed the integers intuitively in a way that would be appropriate for classroom use. Our approach was basically geometric, using the number line to move forwards and backwards and to motivate 'opposites’, addition and subtraction. We wanted the integers to satisfy the usual rules of arithmetic such as the commutative, associative and distributive laws of addition and multiplication, and this insistence led us to the rules for multiplication and division for integers. A careful look at how we derived, for example, the rule that the product of two negative numbers is positive, will reveal that we tacitly used the rules mentioned above when dealing with integers.

In this appendix, we present a more formal construction for the integers using ordered pairs and the idea of an equivalence class. While we hope that teachers find this an interesting approach, (and one which confirms that the rules of integer arithmetic really can be rigorously proven), the material in this appendix is not meant for the classroom.

Ordered Pairs

The starting point is to take the set of ordered pairs (a, b) of whole numbers. Intuitively, we will think of this ordered pair as representing the integer a − b. Thus (7, 4) will be thought of as representing the number 7 − 4 = 3, while (4, 7) will represent the number 4 − 7= −3.

You will immediately realize then, that (5, 3) and (8, 6) both represent the number 2 and so we will say that two ordered pairs (a, b) and (c, d) are equivalent if

a + d = c + b

Note that if a + d = c + b then a − b = c − d, which is what we want.

Addition

We now define the addition of two ordered pairs as follows:

(a, b) + (c, d) = (a + c, b + d).

Hence, for example, (1, 3) + (5, 2) = (6, 5). This will correspond to −2 + 3 = 1.

Notice that since we are using ordered pairs of whole numbers, we can use the usual rules of arithmetic, (the commutative, associative and distributive rules) for the whole numbers. We can see, for example, that the commutative law holds for addition of ordered pairs, since

(a, b) + (c, d) = (a + c, b + d) = (c + a, d + b) = (c, d) + (a, b).

Multiplication

The multiplication rule is a little trickier. To see what the correct definition should be, we recall that (a, b) and (c, d) can be thought of as a − b and c − d, so expanding the product (a − b)(c − d), we obtain ac + bd − ad − bc = ac + bd − (ad + bc).

Hence we define multiplication of the ordered pairs by (a, b).(c, d)= (ac + bd, ad + bc).

Thus, for example, (1, 3).(5, 2) = (5 + 6, 2 + 15) = (11, 17). This corresponds to −2 × 3 = −6.

We can check that the commutative law for multiplication holds, since

(a, b).(c, d)= (ac + bd, ad + bc) = (ca + db, cb + da) = (c, d).(a, b). The second equality uses both the commutative laws for addition and multiplication of whole numbers.

We again stress that all these results are proven assuming only the rules of arithmetic for whole numbers.

Negatives

Next we define the negative of an ordered pair (a, b) by −(a, b) = (b, a).

So, −(a, 0) = (0, a), corresponding to −(a)= −a, and −(2, 6) = (6, 2) which can be thought of as −(−4)= 4.

This enables us to perform subtraction, since we can define

(a, b) − (c, d) = (a, b)+ [−(c, d)] = (a, b) + (d, c) = (a + d, b + c).

Thus (1, 3) − (5, 2)= (3, 8), which corresponds to −2 − 3= −5.

The product of a positive and negative:

Suppose we have the ordered pairs (a, 0) and (0, b). (These ordered pairs correspond to a and −b). When we take their product we obtain

(a, 0) . (0, b) = (0, ab),

and the product corresponds to −ab. This is equivalent to the rule that a positive times a negative is a negative.

For example (4, 0)(0, 3) = (0, 12) corresponding to 4 × (−3) = −12

The product of two negatives:

We can now prove the result corresponding to the rule that the product of two negative numbers is a positive number. Suppose we have the ordered pairs (0, a) and (0, b). (These ordered pairs correspond to negative integers −a and −b). When we take their product we obtain (0, a) . (0, b) = (ab, 0), and the product corresponds to the positive integer ab.

Addition and multiplication are well-defined

The observant reader will realize that we have skipped over a rather important question. Since various ordered pairs can be equivalent, how do we know that the addition and multiplication of equivalent ordered pairs will always produce equivalent ordered pairs? For example,

(6, 3) + (5, 7) = (11, 10).

Now (6, 3) is equivalent to (3, 0) and (5, 7) is equivalent to (0, 2), and

(3, 0) + (0, 2)= (3, 2).

But note that (11, 10) and (3, 2) are equivalent.

Similarly,		(6, 3).(5, 7) = (51, 57)
and		(3, 0).(0, 2) = (0, 6), and (51, 57) is equivalent to (0, 6).

In mathematical language, we say that the definitions of addition and multiplication must be well-defined.

Graphical Representation

These ordered pairs can be viewed graphically as follows.

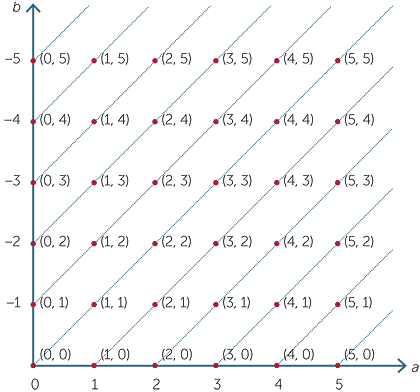
We saw earlier how to tell algebraically when two ordered pairs are equivalent. We can now view this graphically. For example, the ordered pairs

(1, 0), (2, 1), (3, 2), (4, 3), (5, 4) ……..

are all equivalent, and in the diagram we see that they all lie on the dotted line shown. Indeed, the dotted lines in the diagram show lists of equivalent ordered pairs.

The set of all ordered pairs that are equivalent to each other is called an equivalence class. Thus {(1, 0), (2, 1), (3, 2), (4, 3), (5, 4) ……..} is an equivalence class.

We can choose from each equivalence class, any one ordered pair as a representative for that class. Hence (1, 0) (or indeed (5, 4)) is a representative of the equivalence class listed above.

Constructing the Integers

We now see how to recover the whole numbers (and later the integers) from these ordered pairs. Consider each of the ordered pairs lying along the a-axis. Each of these is a representative of an equivalence class. We will identify these ordered pairs with the whole numbers as follows:

(0, 0) 0, (1, 0) 1, (2, 0) 2, (3, 0) 3, (4, 0) 4 etc.

Thus we identify an ordered pair and its equivalence class with a whole number.

Now look at the ordered pairs lying along the b-axis. Each of these is a representative
of an equivalence class. We will identify these ordered pairs with the negative integers
as follows:

(0, 1) −1, (0, 2) −2, (0, 3) −3, (0, 4) −4, (0, 5) −5 etc.

Again, we identify each ordered pair and its equivalence class with a negative number. Notice also that we have exhausted all the ordered pairs using this identification. That is, every ordered pair belongs to an equivalence class which is identified with an integer.

All the rules of integer arithmetic now follow, including the product of two negatives, since we have established these rules for the sets of ordered pairs using only the rules
for whole numbers.

We can construct the number line by rotating the b-axis through 90° as shown:

Ordering of the integers

We conclude this appendix by showing how the ordered pairs can be used to define the ordering relations < and > on the integers.

We will say that (a, b) < (c, d) if a + d < b + c.

For example, (5, 3) < (6, 2), since 7 < 9. This corresponds to 2 < 4 in the integers.

Also (3, 7) < (2, 3) since 6 < 9. This corresponds to −4 < −1 in the integers.

Similarly, we say that (a, b) > (c, d) if a + d > b + c.

For example, (9, 3) > (6, 2), since 11 > 9. This corresponds in the integers to 6 > 4 in
the integers.

You will recall the rule from algebra, that if x < y then −x > −y. We can show this using
the ordered pairs construction.

Suppose that (a, b) < (c, d), then a + d < b + c.

Now −(a, b)	= (b, a)
	> (d, c) (since b + c > a + d)
	= −(c, d)
So −(a, b) >	−(c, d).

 

In an appendix to the module, The Real Numbers we will use a similar approach to construct the fractions from ordered pairs of integers. This will demonstrate that the rational numbers can be logically and rigorously built up from the whole numbers via the integers, using only the basic rules of whole number arithmetic(!). To proceed to the real numbers requires new and more difficult ideas.

ANSWERS TO EXERCISES

EXERCISE 1

n − 7

EXERCISE 2

−3	2	1
4	0	−4
−1	−2	3

EXERCISE 3

−3(5 + (−5)) = 0

−3 × 5 + (−3) × (−5) = 0

−15 + (−3) × (−5) = 0

(−3) × (−5) = 15

EXERCISE 4

a1 b−1

EXERCISE 5

a−45 b−823 c45

EXERCISE 6

a−10 b−n c10d2009

EXERCISE 7

a(a − b) + (c − d) = (a + c ) − (c + d)

EXERCISE 8

[(a, b) + (c, d)] + (e, f)	= (a + c, b + d) + (e, f) = (a + c + e, b + d + f)
	= (a, b) + [(c, d) + (e, f)]

EXERCISE 9

a(65, 45), 5 × 4 = 20 b(46, 71), (−5) × 5 = −25 c(109, 67), (−6) × (−7) = 42

EXERCISE 10

a		[(a, b)(c, d)](e, f)		= (ac + bd, ad + bc)(e, f)
				= (ace + adf + bcf + bde, acf + ade + bce +bdf)
				= (a(ce + df) + b(cf + de), a(cf + de) + b(ce + df))
				= (a, b)[(c, d)(e, f)]
b		(a,b)[(c,d) +(e,f)]		=(a, b)(c + e, d + f)
				= (a(c + e) + b(d + f), a(d + f) + b(c + e))
				= (ac + ae + bd + bf, ad + af + bc + be)
				=(ac + bd, ad+ bc) + (ae +bf, af + be)
				= (a, b)(c, d) + (a, b)(e, f)

EXERCISE 11

(0, b)(a,0) = (0, ab)

EXERCISE 12

Addition well defined

Suppose (a1, b1) is equivalent to (a2, b2) and (c1, d1) is equivalent to (c2, d2)

Then

a1 + b2 = b1 + a2 and c1 + d2 = d1 + c2

(a1, b1) + (c1, d1) = (a1 + c1, b1 + d1)

(a2, b2) + (c2, d2) = (a2 + c2, b2 + d2)

From the first set of equations

a1 + b2 + c1 + d2 = b1 + a2 + d1 + c2

Rearranging

a1 + c1 + b2 + d2 = b1 + d1 + c2+ a2

Therefore

(a1 + c1, b1 + d1) is equivalent to (a2 + c2, b2 + d2)

Multiplication well defined

We will show

(a1, b1) (c1, d1) is equivalent to (a2, b2) (c1, d1)

The result follows easily from this.

(a1, b1) (c1, d1) = (a1c1 + b1d1, b1c1 + a1d1)

(a2, b2) (c1, d1) = (a2c1 + b2d1, b2c1 + a2d1)

We show equivalent.

a1c1 + b1d1 + b2c1 + a2d1	= a1c1 + b2c1+ b1d1 + a2d1
	= c1(b1 + a2) + d1(a1 + b2)		(using the equivalence of (a2, b2) and (c1, d1)
	= c1(b1 + a2) + d1(a1 + b2)
	= c1b1 + c1a2 + d1a1 + d1b2

EXERCISE 13

{(2, 0), (3, 1), (4, 2), …}

EXERCISE 14

a		a − b < c − d is equivalent to a + d < c + b
b		Let (a1, b1) is equivalent to (a2, b2) and (a1, b1) < (c1, d1)
		To show (a2, b2) < (c1, d1)
		We have, a1 + d1 < b1 + c1
		Add b2 to both sides of the inequality.
		a1 + d1 + b2 < b1 + c1 + b2
		By the equivalence a1 + b2 = b1 + a2
		b1 + a2 + d1 < b1 + c1 + b2
		a2 + d1 < c1 + b2
		Hence (a2, b2) < (c1, d1)

EXERCISE 15

(3, 8), (2, 7), (3, 6), (3, 4), (9, 5), (12, 2): (3, 8) is equivalent to (2, 7)

 

The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.

The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.

© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/