The Improving Mathematics Education in Schools (TIMES) Project

return to index

Data Investigation and interpretation

Statistics and Probability : Module 17Year : F-3

June 2011

PDF Version of module

return to top

ASSUMED BACKGROUND

It is assumed that students are familiar in everyday life with gathering and processing simple information such as likes and dislikes of themselves and people and possibly pets in their lives. It is assumed that students are aware of the variation they see in activities and people familiar to them.

return to top

MOTIVATION

Statistics and statistical thinking have become increasingly important in a society that relies more and more on information and demands for evidence. Hence the need to develop statistical skills and thinking across all levels of education has grown and is of core importance in a century which will place even greater demands on society for statistical capabilities throughout industry, government and education.

A natural environment for learning statistical thinking is through experiencing the process of collecting data, exploring data and commenting on data. This is a simple and slightly reduced description of the experience of carrying out real statistical data investigations. Real statistical data investigations start from first thoughts, and then move through planning, collecting and exploring data, to reporting on its features. Statistical data investigations also provide ideal conditions for active learning, hands-on experience and problem solving. Real statistical data investigations involve a number of components:

A number of expressions to summarise the statistical data investigative process have been developed but all provide a practical framework for demonstrating and learning statistical thinking. One description is ‘Problem, Plan, Data, Analysis, Conclusion (PPDAC)’; another is ‘Plan, Collect, Process, Discuss (PCPD)’.

In Years F–3, students start learning and experiencing the elements of gathering and organising information to provide a foundation for developing statistical thinking within the statistical data investigation process across subsequent educational levels.

return to top

CONTENT

In Years F–3, students’ learning experiences start with questions with “yes/no” answers to collect information. They then gradually develop foundations for data investigations through learning experiences in gathering and organising information. The information concerns simple questions in familiar everyday situations where observations fall into simple, natural categories. Students gradually develop through learning experiences in recording and classifying such data, and represent their data in forms that gradually mature from objects and drawings to lists, tables, and picture graphs to column graphs of categorical data.

In Years F–3, we consider only situations involving data where each observation falls into one of a number of distinct categories. Such data are everywhere in everyday life. Some examples are:

Data of this type are called categorical data.

Sometimes the categories are natural or clear, such as with gender or supermarket chain, and sometimes they require choice and description, such as holiday activity.

Another type of data situation in which each observation falls into one of a distinct number of categories is count data. Each observation in a set of count data is a count value. Count data occur in considering situations such as:

Count data in which only a small number of different counts are observed can also be treated as categorical data, particularly for the purposes of data presentations.

This module considers everyday situations involving categorical data and some simple very familiar count data that are treated as falling into categories.

The statistical data investigation process involves:

In F–3, this process is neither followed nor apparent. Rather, the content and experiences of F–3 gradually develop foundations from which students can move to awareness of the statistical data investigation process. This process is used across Years 4-10 to gradually increase understanding, confidence and prowess in statistical concepts, thinking and skills.

In F–3, the focus is on gathering simple information, mostly about the students themselves, and simple ways of organising it. Only information that falls into categories is considered, and there is no thought about any meaning or implications of the information except as it pertains to the students themselves. The questions will mostly be chosen, formed and expressed clearly by the teacher, although as students progress, they can contribute to the choosing of questions and can participate in discussions on how to express a question. Through learning experiences and fun activities, students will also start to develop some understanding of the many challenges in asking and answering questions and organising information from responses to questions.

The examples in this module consider situations familiar and accessible to students in F–3, and gradually progress some of the examples to assist in development of experiences of categorical information and ways of organising it.

Although the sections in this module gradually develop concepts and content over F–3, they are not organised by year level because the content and development of ideas overlap across F–3.

return to top

Yes/no questions

The simplest information-gathering situations are questions with clear yes/no responses. The following are some examples that also quickly start to illustrate how even questions that are apparently simple require care in expression to be explicitly clear.

A
Are you a boy (or a girl)?

B
Are you wearing socks today?

C
Did you bring your hat today?

D
Did you eat cereal for breakfast this morning?

E
Are you the youngest child in your family? (That is, you do not have any younger brothers or sisters.)

F
Are you the oldest child in your family? (That is, you do not have any older brothers
or sisters.)

G
Does your family have any pets?

H
(a more advanced question) Do you usually eat cereal for breakfast?

I
(a more advanced question) Did you go away for last Christmas? (That is, were you away from your (usual) home for all of last Christmas Day?)

Although these are yes/no questions, we see that after the first one, most students are unlikely to answer with a simple yes or no, but provide extra or alternative information. For example, for D, “no, I had egg”, or E, “yes, I have a brother and a sister”. Similarly, information to answer many of the above questions can be obtained by open-ended questions such as “what did you eat for breakfast this morning?”

In addition, when responses are recorded, the initial “raw” information is recorded for each student, and the “no” response on its own tends to have a negative feel to it, with any information as to why it’s “no” being of no interest. However, there are at least two complementary types of ways of handling this to provide rich learning activities that also build a basis for future learning of statistical concepts.

The students can record information either orally, or by choosing or drawing pictures, or by choosing words. Then the children can decide if each answer would be a “yes” or a “no”. For example, for D, each child can say or draw or choose pictures or words to depict what they had for breakfast, and then the group can together say which ones are “yes” to “Did you eat cereal for breakfast this morning?” and which are “no”.

Games can be developed in which only “yes” or “no” is allowed as a response, with accompanying discussion on any subtleties of what comes under the two headings. For example, for D, it is important to understand that the question is inclusive − it is not “Did you eat only cereal for breakfast this morning?” but “Did you eat cereal [and possibly something else also] for breakfast this morning?” Reading the modules in Chance and Data for years beyond Year 4 will show how such early introduction in simple contexts provides a basis for future more explicit understanding of the importance of clear expression in statistical data investigations.

Such games can also be enriched by use of other languages for “yes” and “no”.

Note that these aspects of simple contexts are a reflection of some of the challenges and issues in designing survey questions: should open-ended or closed questions be used? is the question completely clear and does it cover the range of possibilities? is the question respondent-friendly and encouraging of response?

return to top

Presenting information for yes/no questions

The initial recording of information (or data) is always for each person − or, more generally (see modules for Years 4 and above), for each subject. For some examples in the early years, recording information in picture or word form against each name of the students in the class may be sufficient in itself or in combination with yes/no discussions and games.

The next step in presentation can be in pictorial/graphical format in response to a particular yes/no question, with the students’ names arranged vertically above the words “yes” and “no”, as illustrated below for example D.

Did you eat cereal for breakfast this morning?

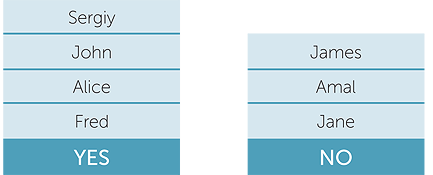
The graph above is under construction, with the first six students allocated to their respective responses. The next step from this is to mark each student with a simple object such as a stick figure, and then a more abstract object such as a *. This step is simply representing the number, or frequency, of students whose response is “yes” or “no”.

return to top

Simple questions with more than
two possible responses

As can be seen above, only some yes/no questions are no more than that. Many arise from questions with more than two possible responses. The following examples are of questions with natural or given categories for responses.

J
What is your favourite colour out of blue, green, and yellow, red?

K
Which of the hats below looks most like your hat?

L
How many brothers and sisters do you have? (0 or 1 or 2 or 3 etc)

M
Does your family buy their fruit and vegetables at supermarket, a fruit and vegetable shop, or another type of shop?

Notice that the categories in L are counts, but are small counts. Example M illustrates a common situation in questions with categorical responses − the need for “other” as a response category.

The initial recording of data for such questions is again for each student, with responses recorded by choosing or using pictures, colours or words, and a list of student names with their responses beside them. For the questions with natural or given response categories, the information can then be presented in pictorial/graphical form as above with more than two categories along the axis, as illustrated below.

What is your favourite colour?

The graph above is under construction, with the first six students allocated to their categories of favourite colour. Similarly to yes/no questions, this pictorial/graphical display can progress to each individual represented by an object such as a stick figure or by a symbol such as a *.

Such information can also be presented in tabular form with the different colours listed in one column and the number of students who responded with that colour listed in the second column. Alternatively, the different colours can be listed in a row, with the numbers for each colour listed in the second row, as below for a class of 25 students.

The next step from questions with natural or given categories is to more open-ended questions which still have just one set of categories as responses, but which require discussion amongst the information gatherers as to how to group the responses. The following questions illustrate some of these types of more open questions.

N
What is your favourite colour?

O
What colour are your eyes?

P
How do you travel to school? (for example: walk, car, bus...)

Q
(more advanced) What did you do in your (last) school holidays?

For questions such as these, after the initial recording or listing of response by each student or against each student’s name, students can check the accuracy of responses for questions such as O and P. They then need to discuss and decide how to classify responses. The classification chosen by students may depend on the range of responses given. For example, in O, students might prefer to distinguish between brown and black in some classes but not in other classes. For N, some students may say colours such as gold or silver and it may be decided to classify them as metallic or it may be decided to classify gold with yellow and silver with white. Orange or brown may be other colours given by one or two students, and, again, whether or how to group these may depend on other colours given, or on the students’ wishes in presenting their information. For P, some students might give a combination, such as “car in the morning, bus in the afternoon”, which students as a group can decide how to classify. For example, they could decide to have a category called “mixed”. Again, how to classify responses to even such simple open-ended questions depends on the variety and nature of the responses. For many of these types of questions, a category of “other” may be chosen.

Such questions and discussion on the variety and range of responses for their individual group is preparing students for the statistical concepts and data handling they will meet from Year 4 onwards.

Once the students decide on their classification of responses, they can present the information as above, using picture graphs and/or tables.

return to top

Next early steps in collecting,
handling and looking at categorical data;
column graphs.

In a number of the above examples, students will tend to give extra information or perhaps to compare responses for boys and girls. Extra information can be recorded and presented in pictures or words for each student, and choices can then be made as to which information or question to focus on for one or more presentations.

For example, the question “Do you have a baby sister or brother?” will produce the information of whether there are any babies, whether the baby is a boy or girl and if there is more than one baby. It will also produce discussion or a query of when is a baby no longer a baby − that is, what classification description of a baby the students wish to use. Perhaps ages under two years old might be considered as “baby”.

The initial listing for each student in response to this question (once the classification is decided) could be presented in a picture as illustrated below. The picture below is under construction, with the responses for the first four students represented pictorially.

Do you have a baby sister or brother?

To see how many students in the class have baby sisters and/or brothers, these data could then be presented in a table as follows.

Number of baby
brothers or sisters 		Number of students
Neither 5
Baby brother 8
Baby sister 6
Baby brother and sister 1
Two baby brothers 3
Two baby sisters 2

This table can be presented graphically similarly to the favourite colours above; the picture below shows the start of building this graph, with the first four students allocated to their response category.

Do you have a baby sister or brother?

For the older students, this graph can be presented in a more efficient and easy to read manner by the following column graph, in which the heights of the columns give the numbers of children in the class with the various categories of baby brothers and sisters.

Chart of babies in family

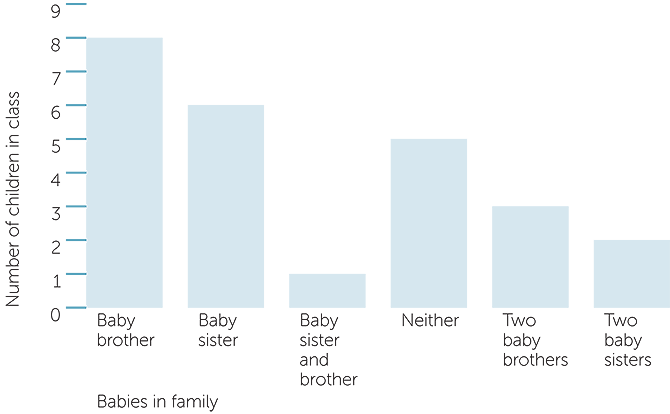
Hence we can read from the column graph that 8 children in the class have a baby brother, 6 have a baby sister, one has a baby brother and a baby sister, etc.

For the question “What is your favourite colour out of blue, green, yellow and red?” the students may be interested in comparing preferences with each other, and in comparing preferences between boys and girls. The table above can have two rows, one for boys and one for girls:

This table can be represented pictorially using symbols or objects or pictures to give the number of boys and girls for each favourite colour, as shown

What is your favourite colour?

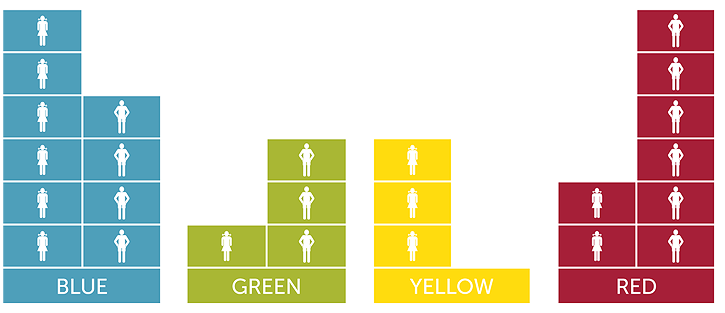
This graph shows that blue and red are the favourite colours overall out of these four colours for this group of students, with two more girls than boys preferring blue, but four more boys than girls preferring red. Of the two lesser preferred colours of yellow and green, boys prefer green and girls prefer yellow.

Notice that the above graph is a column graph with the height of the columns representing the numbers of students in each category.

The question “Does your family have any pets?” will almost certainly produce responses listing the pets. These can be listed through pictures or words for each student. In the yes/no section, the focus is on whether a family has any pets of any description, or no pets. The focus could be on number of pets of any description, in which case, the information for each student would be the number of pets in the family. Or the focus could be on cats and dogs, in which case it may be decided to present the information in terms of the categories: “neither cats nor dogs”; “at least one cat but no dogs”; “at least one dog but no cats”; or “at least one cat and at least one dog”.

If the focus is on number of pets (of any type) in a family, an initial data presentation that corresponds to the listing of pets for each student, could look like the graph below.

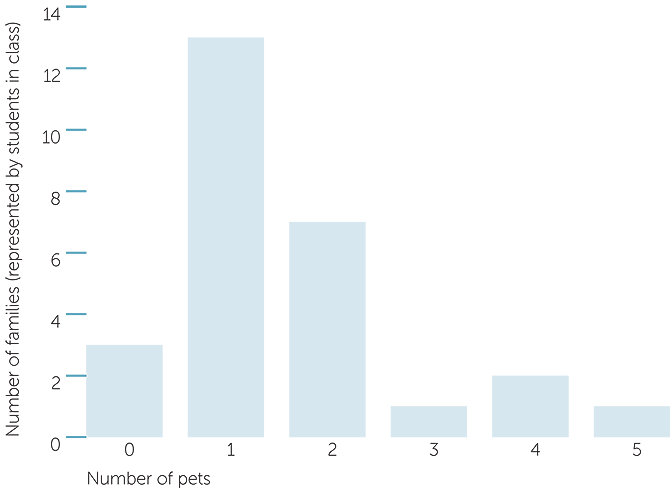
Chart of number of pets

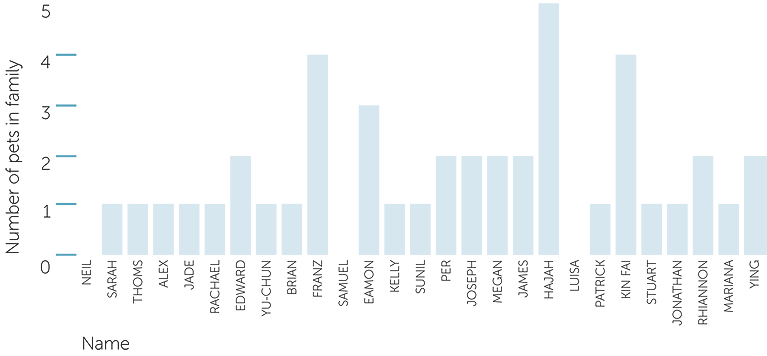
As with previous examples, these data can be presented by a column graph with the heights of the columns giving the number of families (each family being represented by a student in the class) who own the various numbers of pets. We see that there are 3 students whose families have no pets, 11 students whose families own 1 pet, 7 students whose families own 2 pets, 1 with 3 pets, 2 with 4 pets, and 1 with 5 pets.

So the most popular number of pets for a family for students in this class is 1, with the next most popular number of pets being 2.

Chart of number of pets in a family

return to top

A quiz to help your understanding
of some of the above graphs

A teacher asked all the children in her class the question: “How many children are there in your family including yourself?” She made a table of the responses and then used a computer to produce the following two graphs.

Note that there are no children from the same family in this class, e.g. twins.

Graph 1: Chart of children in family

Graph 2: Chart of number of pets in a family

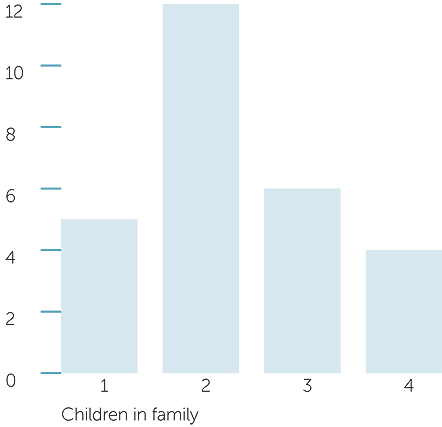
In graph 1, the numbers on the vertical axis represent:

A
the number of children in a family

B
the number of families with a particular number of children

C
the number of children in the class

D
a code that the teacher gave to represent each child

In graph 2, the numbers on the vertical axis represent:

A
the number of children in a family

B
the number of families with a particular number of children

C
the number of children in the class

D
a code that the teacher gave to represent each child

In graph 2, the numbers on the horizontal axis represent:

A
the number of children in a family

B
the number of families with a particular number of children

C
the number of children in the class

D
a code that the teacher gave to represent each child

In order to use graph 1 to determine how many families of the children in the class have more than 3 children, you should:

A
add up the heights of the columns that are higher than 3

B
find the first bar that has a height of 3 and count the number of columns to the right
of that

C
count how many columns are higher than 3

D
arrange the columns from smallest to largest, find the first bar that has a height of
3 and count the number of columns to the right of that

In order to use graph 2 to determine how many families of the children in the class have more than 3 children, you should:

A
count how many columns are higher (on the vertical axis) than 3

B
add up the heights of the columns that are higher (on the vertical axis) than 3

C
count how many columns correspond (on the horizontal axis) to numbers greater than 3

D
add up the heights of the columns that correspond (on the horizontal axis) to numbers greater than 3

E
arrange the columns from smallest to largest, find the first bar that has a height of 3 and count the number of columns to the right of that

Answers (in order of question): A, B, C, D and E

return to top

Some general comments and
links towards years 4 and 5

Across Years F–3, students are gradually introduced to gathering, handling and presenting information in responses to simple everyday questions for which responses fall into categories. The questions and information are mostly gathered from themselves. Because the responses to such everyday questions in conversation usually contain more information than merely a “yes” or “no” or single word response, the learning experiences in F–3 move gradually from listing information for each student, in the form of pictures or objects and later moving on to words, to choosing the relevant information to answer questions and classify responses where necessary. The initial questions are simple “yes/no” questions. The next step is to questions with possible responses falling into simple natural or given categories. Learning experiences then develop with questions for which classifications or categories need to be chosen or decided. Finally, some situations are considered in which a secondary classification is also of interest, either in creating more refined categories (such as baby sister, baby brother, etc) or in including the secondary classification through pictures or other symbols or colours (such as the pictures of boys and girls in presenting information on favourite colour).

Students learn how to turn listings of information for each individual into tables, picture graphs and then column graphs, where the graph presents the number of responses that fall into each category.

Thus in F–3 only simple categorical data are used, even if responses to questions may contain more information that requested or needed. Many learning experiences in which students move from recording information for each individual to presenting − whether pictorially or graphically − the number of responding individuals in each category, provide valuable underpinning for learning about statistical data investigations and interpretations in Years 4-10.

Although simple categorical data are used in Years F–3, the content of Year 4 marks the first experiences in the process of statistical data investigations. The focus is on considering just one categorical variable at a time, so that the only types of presentations are tables and column graphs with just one set of categories, but in a more general framework with statistical concepts and in the context of statistical data investigations. Even in this relatively simple situation the examples of Year 4 illustrate the extent of statistical thinking involved in the initial stages of an investigation in identifying the questions/issues and in planning and collecting the data.

From Year 4 onwards, students also increasingly consider concepts such as ‘what do our data represent’ and variation in data across samples. Variation in data across samples tends to arise naturally in everyday situations that are very familiar to young students. These concepts are further developed as students progress.

In Year 5, we extend the concepts of types of data to consider measurement data and more general situations with count data. In Year 5, although questions and issues may involve more than one variable, the focus is on exploring and interpreting phases of the investigation process with one variable at a time. Year 6 introduces the concept of association between two categorical variables.

 

The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.

The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.

© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/

Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.

AMSI ICE-EM