The Improving Mathematics Education in Schools (TIMES) Project
Cones, pyramids and spheres
Measurement and Geometry : Module 12![]() Years : 9-10
Years : 9-10
June 2011
- Familiarity with calculating the areas of the standard plane figures including circles.
- Familiarity with calculating the volume of a prism and a cylinder.
- Familiarity with calculating the surface area of a prism.
- Facility with visualizing and sketching simple three-dimensional shapes.
- Facility with using Pythagoras’ theorem.
- Facility with rounding numbers to a given number of decimal places
or significant figures. - Facility with manipulation of formulas and equations
In the earlier module, Area Volume and Surface Area we developed formulas and principles for finding the volume and surface areas for prisms. The volume of a prism, whose base is a polygon of area A and whose height is h, is given by
![]() Volume of a prism = Ah.
Volume of a prism = Ah.
This formula is also valid for cylinders. Hence, if the radius of the base circle of the cylinder is r and its height is h, then:
![]() Volume of a cylinder = πr2h
Volume of a cylinder = πr2h
Also in that module, we defined the surface area of a prism to be the sum of the areas of all its faces. For a rectangular prism, this is the sum of the areas of the six rectangular faces. For other prisms, the base and top have the same area and all the other faces are rectangles.
In this module, we will examine how to find the surface area of a cylinder and develop the formulae for the volume and surface area of a pyramid, a cone and a sphere. These solids differ from prisms in that they do not have uniform cross sections.
This will complete the discussion for all the standard solids.
Pyramids have been of interest from antiquity, most notably because the ancient Egyptians constructed funereal monuments in the shape of square based pyramids several thousand years ago. Conical drinking cups and storage vessels have also been found in several early civilisations, confirming the fact that the cone is also a shape of great antiquity, interest and application. The word sphere is simply an English form of the Greek sphaira meaning a ball.
Conical and pyramidal shapes are often used, generally in a truncated form, to store grain and other commodities. Similarly a silo in the form of a cylinder, sometimes with a cone on the bottom, is often used as a place of storage. It is important to be able to calculate the volume and surface area of these solids.
The ancient Greeks discovered the various so-called quadratic curves, the parabola, the ellipse, the circle and the hyperbola, by slicing a double cone by various planes. Of these, the parabola, obtained by slicing a cone by a plane as shown in the diagram below, is studied in some detail in junior secondary school. These conic sections, as they are also called, all occur in the study of planetary motion.
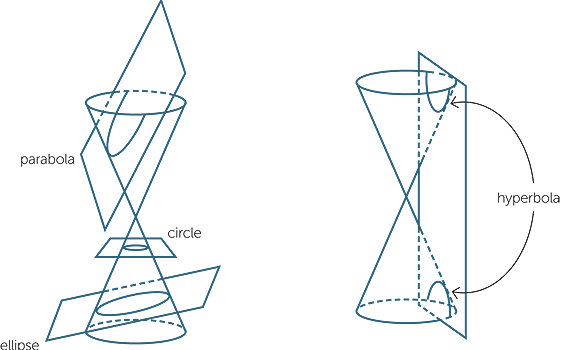
The sphere is an example of what mathematicians call a minimal surface. The sphere is a smooth surface that bounds a given volume using the smallest surface area, just as the circle bounds the given area using the smallest perimeter. The sphere is a three-dimensional analogue of the circle. As we saw in the module, The Circle, we use the word sphere to refer to either the closed boundary surface of the sphere, or the solid sphere itself.
Suppose we have a cylinder with base radius r and height h. If we roll the cylinder along a flat surface through one revolution, as shown in the diagram, the curved surface traces out a rectangle.
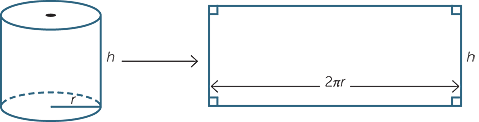
The width of the rectangle is equal to the height of the cylinder. The length of the rectangle is equal to the circumference of the circle, which is 2πr. Hence the area of the curved portion of the cylinder is 2πrh. Adding in the area of the circles at each end of the cylinder, we obtain,
![]() Surface Area of a cylinder = 2πrh + 2πr2.
Surface Area of a cylinder = 2πrh + 2πr2.
EXAMPLE
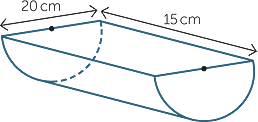
Calculate the surface area of each solid, correct to 2 decimal places.
a |
 |
b |
|
SOLUTION
a |
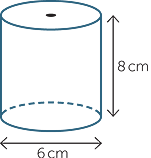
Here, r = 3 and h = 8. | ||||
| Surface area | = 2πrh + 2πr2 | ||||
| = 2 × π × 3 × 8 + 2 × π × 32 | |||||
| = 66π cm2 | |||||
|
≈ 207.35cm2 | (to 2 decImal places). | |||
b |
Here, r = 10 and h = 15. | |||
| Area of curved section | = 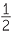 × 2πrh = 150π cm2 × 2πrh = 150π cm2 |
|||
| Area of top rectangle | = 300 cm2 | |||
| Area of two semicircles | = πr2 | |||
| = 100π cm2 | ||||
| Surface area | = (250π + 300) cm2 | |||
|
≈ 1085.40 cm2 | (to 2 decimal places). |
If the base of a pyramid is a regular polygon, then it has a well-defined centre. If the vertex of the pyramid lies vertically above the centre, then the pyramid is called a right pyramid. In most of what follows, we assume the pyramid is a right pyramid.
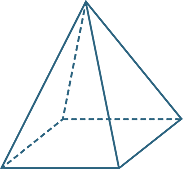
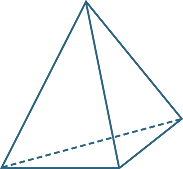
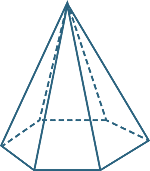
A pyramid is a polyhedron with a polygonal base and triangular faces that meet at a point called the vertex. The pyramid is named according to the shape of the base.
![]()
![]()
square-based pyramid ![]() triangular-based pyramid
triangular-based pyramid ![]() hexagonal-based pyramid
hexagonal-based pyramid
If we drop a perpendicular from the vertex of the pyramid to the base, then the length of the perpendicular is called the height of the pyramid.
Surface area of a right pyramid
The faces bounding a right pyramid consist of a number of triangles together with the base. To find the surface area, we find the area of each face and add them together. Depending on the information given, it may be necessary to use Pythagoras’ Theorem to calculate the height of each triangular face. If the base of the pyramid is a regular polygon, then the triangular faces will be congruent to each other.

EXAMPLE
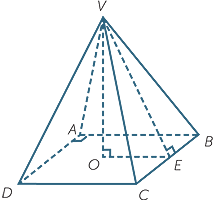 VABCD is a square-based pyramid with vertex V and
VABCD is a square-based pyramid with vertex V and
base ABCD, with V vertically above the centre of the
square base. The height of the pyramid is 4 cm and
the side length of the base is 6 cm, find the surface
area of the pyramid.
Solution
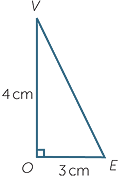 We need to find the height VE of triangle VBC,
We need to find the height VE of triangle VBC,
using Pythagoras’ Theorem.
| VE2 | = VO2 + OE2 |
| = 42 + 32 | |
| = 25 |
Hence VE = 5 cm.
| Area of VCB |
= 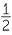 × CB × VE × CB × VE
|
= 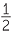 × 6 × 5 × 6 × 5
|
|
| = 15 cm2 | |
| Area of base | = 6 × 6 |
| = 36 cm2 | |
| Surface area | = 4 × 15 + 36 |
| = 96 cm2 |
EXERCISE 1
When it was built, the Great Pyramid of Cheops in Egypt had a height of 145.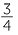 m and its base was a square of side length 229 m. Find its surface area in square metres, correct to three significant figures.
m and its base was a square of side length 229 m. Find its surface area in square metres, correct to three significant figures.
Volume of a pyramid
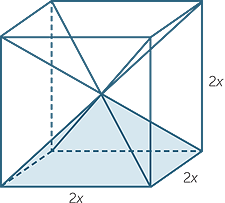
Here is a method for determining the formula for the volume of a square-based pyramid.
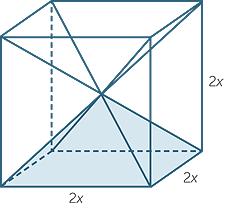 Consider a cube of side length 2x. If we draw the four long diagonals as shown, then we obtain six square-based pyramids, one of which is shaded in the diagram.
Consider a cube of side length 2x. If we draw the four long diagonals as shown, then we obtain six square-based pyramids, one of which is shaded in the diagram.
Each of these pyramids has base area 2x × 2x and height x. Now the volume of the cube is 8x3. So the volume of each pyramid is  × 8x3 =
× 8x3 = 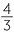 x3. Since the base area of each pyramid is 4x2 it makes sense to write the volume as
x3. Since the base area of each pyramid is 4x2 it makes sense to write the volume as
![]() Volume =
Volume =  × 4x2 × x =
× 4x2 × x =  × area of the base × height.
× area of the base × height.
We can extend this result to any pyramid by using a geometric argument, giving the following important result.
![]() Volume of a pyramid =
Volume of a pyramid =  × area of the base × height.
× area of the base × height.
See the appendix on the pyramid for details.
EXERCISE 2
Find the volume of the Great Pyramid of Cheops whose height is 145.75 m and whose base is a square of side length 229 m. Give answer in cubic metres correct to two significant figures.
EXERCISE 3
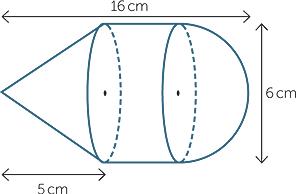
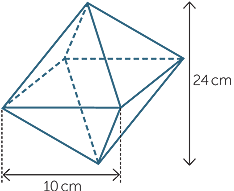 Find the volume of the ‘diamond’, with height 24 cm and side length 10 cm as shown.
Find the volume of the ‘diamond’, with height 24 cm and side length 10 cm as shown.
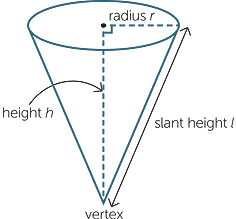
To create a cone we take a circle and a point, called the vertex, which lies above or below the circle. We then join the vertex to each point on the circle to form a solid.

If the vertex is directly above or below the centre of the circular base, we call the cone a right cone. In this section only right cones are considered.
If we drop a perpendicular from the vertex of the cone to the circular base, then the length of this perpendicular is called the height h of the cone.
The length of any of the straight lines joining the vertex to the circle is called the slant height of the cone. Clearly l2 = r2 + h2 , where r is the radius of the base.
Surface area of a cone
Suppose the cone has radius r, and slant height l, then the circumference of the base of the cone is 2πr.
To find the area of the curved surface of a cone, we cut and open up the curved surface to form a sector with radius l, as shown below.
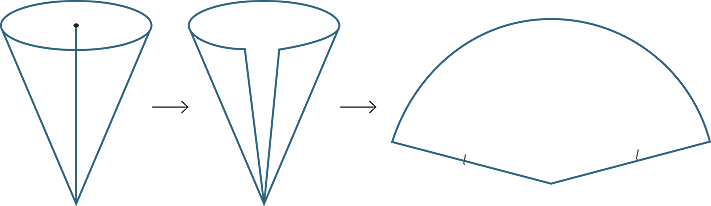
In the figure to the right below the ratio of the area of the shaded sector to the area of the circle is the same as the ratio of the length of the arc of the sector to the circumference of the circle.
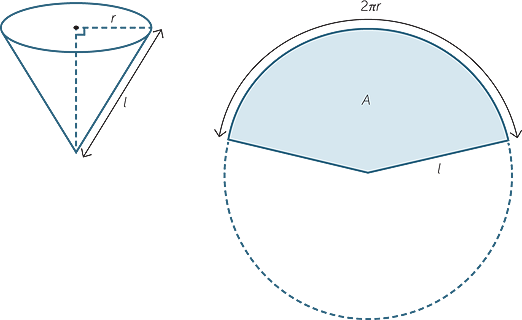
Thus the fraction of the area of the whole circle taken up by the sector is
![]()
 =
= 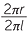 .
.
Hence, the area of the sector is 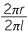 × πl2 = πrl.
× πl2 = πrl.
In conclusion, the area of the curved surface of the cone is πrl
Adding this to the base, we have
![]() Surface area of a cone = πrl + πr2.
Surface area of a cone = πrl + πr2.
EXERCISE 4
Find the surface area of the solid with dimensions shown.
Volume of a cone
When developing the formula for the volume of a cylinder in the module Area Volume and Surface Area, we approximated the cylinder using inscribed polygonal prisms. By taking more and more sides in the polygon, we obtained closer and closer approximations to the volume of the cylinder. From this, we deduced that the volume of the cylinder was equal to the area of the base multiplied by the height.
We can use a similar approach to develop the formula for the volume of a cone.
Given a cone with base radius r and height h, we construct a polygon inside the circular base of the cone and join the vertex of the cone to each of the vertices of the polygon, producing a polygonal pyramid. By increasing the number of sides of the polygon, we obtain closer and closer approximations to the cone. Hence,
![]() Volume of a cone =
Volume of a cone =  × area of the base × height
× area of the base × height
![]() =
=  πr2h
πr2h
EXERCISE 5
Find the volume of the solid described in the previous exercise.
Oblique Prisms, Cylinders and Cones
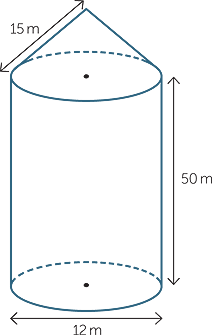
We have seen that the volume of a right rectangular prism is area of the base multiplied by the height. What happens if the base of the prism is not directly below the top?
Cavalieri’s first principle states that if the cross-sections of two solids, taken at the same distance above the base, have the same area, then the solids have the same volume.
We will not give a proof of Cavalieri’s principle here. To present a rigorous proof requires integration and slicing ideas.
It allows us to say that the volume of any rectangular prism, right or oblique, is given by the area of the base multiplied by the height.
The same applies to oblique cylinders and cones.
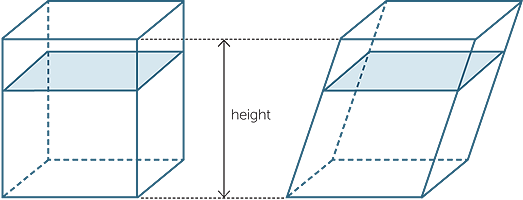
EXAMPLE
 Find the volume of the cylinder shown in the diagram.
Find the volume of the cylinder shown in the diagram.
Solution
The volume of the cylinder is V = π × 52 × 15 = 375π cm2.
Cavalieri’s second principle states that if the cross-sections of two solids, taken at the same distance above the base, have areas in the ratio a:b, then the solids have the volumes in the ratio a:b.
EXERCISE 6
We showed earlier that the volume of a square based pyramid with base length 2x and height x has volume  × 2x × 2x × x. Use Cavalieri’s second principle to show that the volume of a pyramid whose base is a rectangle with side lengths c and d and height h is
× 2x × 2x × x. Use Cavalieri’s second principle to show that the volume of a pyramid whose base is a rectangle with side lengths c and d and height h is  × cd × x.
× cd × x.
A sphere is the set of all points in three-dimensional space whose distance from a fixed point O (the centre), is less than or equal to r (the radius).
Every point on the surface of the sphere lies at distance r from the centre of the sphere.
We will derive the surface area formula from the volume formula.
Volume of a sphere
The easiest and most natural modern derivation for the formula of the volume of a sphere uses calculus and will be done in senior mathematics. A derivation using a clever application of Cavalieri’s principle is discussed in the History section of this module.
The volume of a sphere radius is given by
![]() Volume of a sphere of radius r=
Volume of a sphere of radius r= 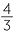 πr3.
πr3.
EXAMPLE
a![]() Calculate the volume of the a sphere with a diameter of 30 m.
Calculate the volume of the a sphere with a diameter of 30 m.
b ![]() A sphere has volume 2800 cm3. Find the radius of the sphere, correct to the nearest millimetre.
A sphere has volume 2800 cm3. Find the radius of the sphere, correct to the nearest millimetre.
Solution
| a | The radius is 15 m. | ||||
| V | = 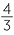 πr3 πr3 |
||||
= 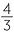 × π × 153 × π × 153 |
|||||
| = 4500π m3 | |||||
| b | V | = 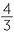 πr3 πr3 |
|||
| 2800 | = 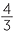 πr3 πr3 |
||||
| so r3 | = 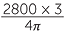 |
||||
| r | = 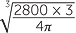 |
||||
| ≈ 8.7 cm | (correct to 1 decimal place). | ||||
The radius is approximately 87 mm.
Surface area of a sphere
Calculus is needed to derive the formula for the surface area of a sphere rigorously. Here is a interesting formula that uses the idea of approximating the sphere by pyramids with a common vertex at the centre of the sphere.

Consider a sphere of radius r split up into very small pyramids, as shown. The volume of each pyramid is equal to  Ar, where A is the area of the base. Suppose there are n of these pyramids in the sphere, each with base area A.
Ar, where A is the area of the base. Suppose there are n of these pyramids in the sphere, each with base area A.
Hence the total volume of these pyramids is  rnA.
rnA.
The more pyramids we take, the closer this will be to the volume of the sphere.
Also the sum of the areas of the bases, nA will get closer to the surface area of the sphere, S. Hence, using the formula for the volume of the sphere, we have
![]()
 rS =
rS = 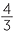 πr3, giving S = 4πr2.
πr3, giving S = 4πr2.
Hence the surface area of a sphere radius r is
![]() Surface area = 4πr2.
Surface area = 4πr2.
EXAMPLE
Calculate, correct to 2 decimal places, the surface area of a sphere with diameter 10 cm.
Solution
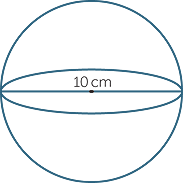 The diameter is 10 cm, so r = 5 cm.
The diameter is 10 cm, so r = 5 cm.
Then S = 4πr2
= 4 × π × 52
= 100π cm2
≈ 314.16 cm2 (correct to 2 decimal places).
The surface area is approximately 314.16 cm2.
EXERCISE 7
Find the surface area and volume of the following:
As promised in the Motivation, we have now completed the mensuration formulae of all the standard two and three-dimensional objects. Nevertheless, there are other objects that occur in everyday life whose areas and volumes we cannot find using these formulae and methods alone. Once such example are the `sails’ on the Opera House in Sydney.
Here is another.
Suppose we ‘half-fill’ a glass with water. Supposing the glass is a cylinder of radius r and height h, and suppose the water covers exactly half of the circular base, what is the volume of the water?
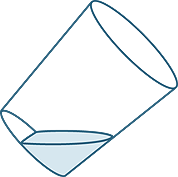
This problem was posed and solved by Archimedes. It is usually solved today using slicing techniques from integral calculus.
Slicing techniques in calculus exploit the idea we saw when finding the volume of a prism or a cylinder. If we can find the volume of a typical slice of the solid, then, assuming the solid has uniform cross-section, we can add all the slices to find the volume. In calculus, we find the volume, in terms of a variable x, of a typical slice whose thickness, written as δx, is very small. We can then integrate this to obtain the total volume. This method can be used very effectively to find the volume of solids which do not have uniform cross-section, and may have curved boundaries.
One simple application of this method allows us to find the volume of any solid that is formed by rotating part of a curve, y = f(x), in the xy-plane, between x = a and x = b, around the axis.
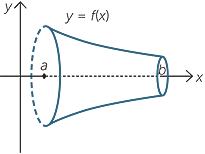
Those familiar with integral calculus will recognize the following formula for the volume of such a solid of revolution.
![]() Volume =
Volume = 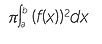 .
.
Here, the thin slice of thickness δx is approximately a cylinder with base radius f(x) and so the volume of the slice is approximately π (f(x))2δx.
If we take the circle centre the origin and radius r, then its Cartesian equation is x2 + y2 = r2. A sphere of radius can then be formed by rotating this circle about the x-axis. Thus, its volume is found by computing the integral
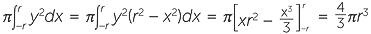
after simplification.
More on cones
The portion of a right cone remaining after a smaller cone is cut off is called a frustum. Suppose the top and bottom of a frustum are circles of radius R and r, respectively, and that the height of the frustum is h, while the height of the original cone is H. The volume of the frustum is by the difference of the volumes of he two cones and is given by
![]() Volume of a frustum =
Volume of a frustum =  π[H(R2 − r2) + r2h].
π[H(R2 − r2) + r2h].
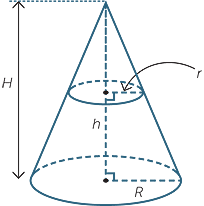
Using similar triangles, we can eliminate H and the formula can be rewritten as
Volume of a frustum =  πh(R2 + r2 + rR).
πh(R2 + r2 + rR).
EXERCISE 8
Derive these results.
Similarly, it can be shown that the surface area of the frustum of a cone with base radii r and R and slant height s, is given by
![]() Surface Area of a frustum = π(r2 + R2) + π(r + R)s.
Surface Area of a frustum = π(r2 + R2) + π(r + R)s.
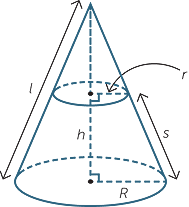
Note that when r = l we obtain the surface area of a cylinder.
EXERCISE 9
Derive this formula.
The concepts and insights developed in finding the formulas for areas and volumes are used in Physics and Engineering to find such quantities as the centre of mass and the moment of inertia of a solid body. Thus the development of volume formulas are important for students, as is the careful memorizing of the key formulas, such as the volume of a sphere.
Archimedes gave a geometric demonstration that the surface area of a sphere with radius r was equal to the area of the curved surface of the cylinder into which the sphere exactly fits.
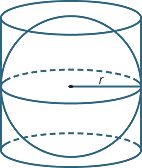
EXERCISE 10
Assuming Archimedes’ result, derive the formula for the surface area of the sphere.
The formula for the volume of a sphere can be found with a striking application of Cavalieri’s first principle as follows:
Take a hemisphere of radius and look at the area of a typical cross-section at height above the base.

Also consider a cylinder of height h and radius r, with a cone of the same height
and radius removed.
EXERCISE 11
a ![]() Show that the area of the circular cross-section of the hemisphere at height h
Show that the area of the circular cross-section of the hemisphere at height h
is given by π(r2 − h2).
b ![]() Show that the area of the cross-section of the cylinder with the cone removed at height h is also π(r2 − h2).
Show that the area of the cross-section of the cylinder with the cone removed at height h is also π(r2 − h2).
c ![]() Use Cavalieri’s principle to deduce that these solids have the same volume and hence find derive the formula for the volume of the sphere.
Use Cavalieri’s principle to deduce that these solids have the same volume and hence find derive the formula for the volume of the sphere.
The later Greek Mathematician Pappus (290-350 AD) discovered the following remarkable method for finding the volume of a solid of revolution generated by rotating a plane region with area A about a fixed axis.
The volume of the solid is equal to the product of the area A of the plane region and the distance travelled by its geometric centroid as it moves through one revolution. The centroid is another word for centre of mass. This method can be used to find the volume of a torus (a Latin word meaning couch), which is the solid obtained by rotating a circle about a line external to the circle.

Suppose that we rotate a circle of radius r about a vertical line whose distance from the centre of the circle is R. The centroid of the circle is simply the centre of the circle and so as the circle is rotated about the line, the centroid will trace out another circle of radius R and which has circumference 2πR. Since the area of the rotated circle is πr2, Pappus’ theorem tells us that the volume of the torus is
![]() 2πRπr2 = 2π2r2R.
2πRπr2 = 2π2r2R.
Pappus also showed that the surface area of a solid of revolution is equal to the product of the perimeter of the plane region being rotated and the distance travelled by its geometric centroid as it moves through one revolution.
EXERCISE 12
Show that the surface area of the torus is given by 4π2rR.
Little further progress was made with volumes and surface areas until the development of the Calculus. The theory of several variable calculus enables more complicated volumes and surface areas to be calculated and the concept of area and volume to be generalised to higher dimensions.
Modern analysis is that branch of mathematics and studies and develops ideas from calculus. Using calculus, the theory of integration generalises the notions of area and volume. Measure Theory, a branch of modern analysis beginning the work of Henri Lebesgue, (d. 1910), generalises the notions of the integral.
In the section Pyramids, we showed that a pyramid whose base is a square of sides 2x × 2x and height x has volume  × 2x × 2x × x which is
× 2x × 2x × x which is  base × height.
base × height.
In this appendix, we will show how to extend this result to any rectangular based pyramid.
It can also be shown that the volume of any pyramid is given by  × area of base × perpendicular height.
× area of base × perpendicular height.
Cavalieri’s first principle states that given two solids of the same height, whose cross-sections, taken at the same distance above the base, are of equal area, then the solids have the same volume.
Cavalieri’s second principle states that if the cross-sections of two solids taken at the same distance above the base have areas in the ratio a:b, then the solids have their volumes in the ratio a:b.
We will use the second principle to show that the formula holds for any square pyramid of height h.
Take two square pyramids of height h, one with base square length 2h and one with base square length 2l. From our earlier discussion, we know that the volume of the first pyramid is
V1 =  × 4h2 × h. Let V2 be the volume of the second pyramid.
× 4h2 × h. Let V2 be the volume of the second pyramid.
Take a slices at B and B1, distance d from the vertices, as shown in the diagram,
so that AB = A1B1 = d.
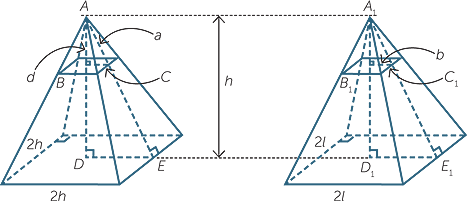
Let BC = a, B1C1 = b. Referring to the diagrams,  ABC is similar to
ABC is similar to  ADE.
ADE.
Hence 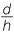 =
=  implies a = d.
implies a = d.
Hence the area of the cross-section for the first pyramid is given by 4a2 but this equals 4d2.
Now in the second pyramid,  A1B1C1 is similar to
A1B1C1 is similar to  A1D1E1.
A1D1E1.
Hence 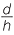 =
= 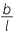 implies b =
implies b = 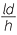
Thus the area of the cross-section is 4b2 but this equals 4l2d2. Now the ratios of the areas is 4a2:4b2 = 4d2: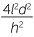 = h2:l2.
= h2:l2.
This ratio is independent of d and so from Cavalieri’s second principle, the ratio of the volumes is also h2:l2. This gives us
![]()
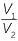 =
= 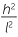
Hence V2 = 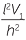 =
=  × 4l2 × h which is
× 4l2 × h which is  × base × perpendicular height.
× base × perpendicular height.
This tells us that the formula  × base × perpendicular height is valid for a square pyramid of height h.
× base × perpendicular height is valid for a square pyramid of height h.
Suppose we have two pyramids, one with a square base side length 2x and height h and one whose base is a rectangle with sides 2y × 2z, also of height h. The volume of the first pyramid is  × 4h2 × h by our discussion above.
× 4h2 × h by our discussion above.
We can choose x such that 4x2 = 4yz, so that the area of the rectangle equals the area of the square.
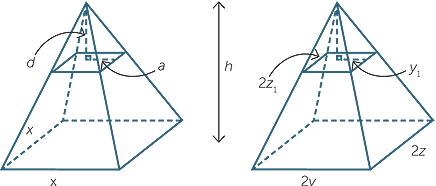
Take slices at a distance d from the vertex in each pyramid. Using similar triangles, we can easily show that so 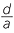 =
= 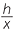 and a =
and a = 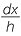 . Thus the area of the cross-section in the first pyramid is
. Thus the area of the cross-section in the first pyramid is
A1= 4a2= 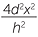 .
.
In the second pyramid, we can again use similar triangles, as we did above, to show that
y1 = 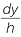 . Similarly, if z1 is half the width of the rectangular slice, then z1 =
. Similarly, if z1 is half the width of the rectangular slice, then z1 = 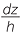 giving the area of the cross-section to be 4y1z1 =
giving the area of the cross-section to be 4y1z1 = 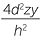 .
.
Since zy = x2, the cross-sections are equal in area and since the pyramids have the same height, their volumes are equal by Cavalieri’s first principle. Thus the volume of the rectangular pyramid is  × 2y × 2z × h, or
× 2y × 2z × h, or  × base area x height.
× base area x height.
It remains to say that a similar method can be used to progress from a pyramid with rectangular base to one whose base is a regular polygon, although the technical details are more complicated and will not be given here.
A History of Mathematics: An Introduction, 3rd Edition, Victor J. Katz, Addison-Wesley, (2008)
History of Mathematics, D. E. Smith, Dover publications New York, (1958)
EXERCISE 1
137 000 m2
EXERCISE 2
2 500 000 m3
EXERCISE 3
800 cm3
EXERCISE 4
726π m2
EXERCISE 5
(1800 + 36 )π m3
)π m3
EXERCISE 6
The ratios of the areas of the cross-sections taken at the same heights is 4x2: cd
From Cavalieri’s second principle:
Volume of pyramid = 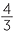 x3 ×
x3 × 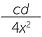 =
=  cdx
cdx
EXERCISE 7
Surface area =(3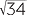 + 66)π cm2
+ 66)π cm2
Volume = 105π cm3
EXERCISE 8
Volume of frustrum = volume of large cone − Volume of small cone
![]() =
=  πR2H −
πR2H −  πr2(H − h)
πr2(H − h)
![]() =
=  π((R2 −r2)H + r2h)
π((R2 −r2)H + r2h)
By similarity, H = 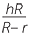 . Substituting in the above formula gives the result.
. Substituting in the above formula gives the result.
EXERCISE 9
Surface area of the frustrum = π(r2 + R2) + πRl − πr(l − s)
By similar triangles, Rs = Rl − lr
π(r2 + R2) + πRl − πr(l − s) = π(r2 + R2) + π(r + R)s
EXERCISE 10
2π × r × 2r = 4πr2
EXERCISE 11
a The square of the radius of the cross-section = r2 − h2 (By Pythagoras’ theorem)
Area of cross-section= π(r2 − h2)
b Area of cross-section = πr2 − πh2
c Volume of cylinder − volume of cone = πr3 −  πr3 =
πr3 = 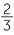 πr3
πr3
EXERCISE 12
Surface area = 2πr × 2πR = 4π2rR
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()