The Improving Mathematics Education in Schools (TIMES) Project
Years : 1-3
It is assumed that students have heard and used in everyday conversation words such “will”, “won’t”, “might”, and have heard and perhaps used words such as “likely”, “unlikely”, “certain” and “impossible”.
Statistics and statistical thinking have become increasingly important in a society that relies more and more on information and calls for evidence. Hence the need to develop statistical skills and thinking across all levels of education has grown and is of core importance in a century which will place even greater demands on society for statistical capabilities throughout industry, government and education. And because the concepts and thinking of statistics take time and many and varied learning experiences to grow the necessary familiarity and confidence, it is important that they are developed in a gradual and coherent manner throughout schooling.
Statistics is the science of variation and uncertainty. Concepts of probability underpin all of statistics, from handling and exploring data to the most complex and sophisticated models of processes that involve randomness. Concepts of probability also inform our everyday living and planning and understanding of risk, chance and variation.
Probability is a measure, like length or area or weight or height, but a measure of the likeliness or chance of possibilities in some situation. It is not a physical measure and hence its concepts require careful and steady development. Probability is a relative measure; it is a measure of chance relative to the other possibilities of the situation. Comparisons of probabilities are therefore fundamental to any concepts or assignations of probabilities.
Chance and data are inextricably linked and integrated throughout statistics.
The objectives of the chance and probability strand of the F-10 curriculum are to provide a practical framework for experiential learning in foundational concepts of probability for life, for exploring and interpreting data, and for underpinning later developments in statistical thinking and methods, including models for probability
and data.
In this module, in the context of starting to develop understanding of chance in everyday life, we consider familiar and everyday events involving chance and use language such as “will happen”, might happen”, progressing to “likely” or “unlikely”. We identify some events that “won’t happen”, progressing to identifying events that are “certain” or “impossible”.
From describing the likeliness of events we observe, we progress in Year 3 to devising
and conducting activities involving chance, and observing variation in the results of
these activities.
Year 1: “Will, won’t, might happen”
In preparing for concepts of chance, awareness of how we describe the likeliness of events and how this description can depend on context and small details in everyday speech, help to form the start of our thinking. Questioning whether statements are specific or more general can also lay the foundation for awareness of care needed in making general statements and of being clear about the situation being considered.
Just how much comes under the banner of “might happen” lays the foundation for needing more language and then better and clearer ways of describing chances of all
the different types of events that are not “will happen” or “won’t happen”.
Below are a variety of statements about everyday events illustrating use of “will, won’t, might, happen”.
A baby will need its nappy changed sometime during the day.
My baby sister might need her nappy changed when she wakes up.
It might rain today.
The sun will set tonight.
The sun will rise tomorrow morning.
The traffic lights will change from red to green.
The traffic lights won’t change from red to blue.
Our dog will want dinner tonight.
Our dog won’t refuse to eat his dinner.
Our dog might tip his bowl over.
A cat might miaow tonight for his dinner.
A cat might eat all his dinner.
Our cat won’t tip his bowl over.
My mother says we will be going shopping after school today.
A mother might be late getting to school this afternoon.
Notice that some of these statements refer to restricted situations − for example,
“Our dog ….” or “…today” - and some refer to more general situations, such as
“The sun….” or “A baby…”.
Students will be able to think of many similar statements and compare their statements with each other. Some statements referring to themselves, their families and their lives may be “will” or “won’t” statements in general, and some will refer to specific times or places. Similarly, in comparing statements with each other, students will find that some are specific to them, and some may be able to be generalised, but many will need to be “might happen” statements to apply across students.
Year 2: “Likely, unlikely, certain, impossible”
From “will, won’t, might”, we move on to the language of chance with “certain” and “impossible”, and start considering more closely the many events that “might happen” in terms of what could be considered “likely” and what could be considered “unlikely”.
In considering certainty and impossibility in everyday events, students learn the difference between impossible and “very unlikely but can’t be designated as impossible”. Similarly, students learn the difference between certainty and “highly likely but can’t be designated as certain”.
In considering what is unlikely and what is likely, students will not necessarily agree, and may tend to argue from their own experiences or the context. Referring to context is important and necessary, and arguing from personal experience helps in the learning of the need for information − whether this is in the form of data or assumptions.
Below are some statements and questions for students to agree with, disagree with,
or discuss.
It is impossible for a river to flow up a hill.
It is certain that it is colder at the South Pole than at the equator.
It is impossible for a newborn baby to look after itself.
It is certain that a newborn baby will grow.
It is impossible for fish to live (all the time) outside water.
Is it certain that meat will go bad if it is left out of the fridge?
Is it certain that you will get wet if you stand in the rain?
Is it certain that a ball will fall down after you throw it?
A ball is likely to bounce when it is dropped.
It is likely that a loud noise will wake a baby.
It is likely that I will catch a cold if someone with a cold sneezes on me.
It is unlikely I will travel to the moon.
In Australia, it is likely to be colder in July than it is in January.
In Australia, it is likely to be cooler at Easter than at Christmas.
A cat is unlikely to chase a dog.
A cat is likely to chase a mouse.
Thunder and lightning are likely during a storm.
It is unlikely I will be awake at midnight.
It is likely that a dog will bark at a stranger.
It is likely that my big sister will want to buy new clothes.
It is unlikely that a family will go on a trip to the North Pole.
It is unlikely that I will meet the Prime Minister.
It is likely we will go swimming in summer.
If I bring my hat to school, it is likely I will be allowed to play outside at lunchtime.
If I run too fast, I am likely to trip.
Students will be able to think of many similar statements and compare their statements with each other. Some events that they may be tempted to describe as certain or impossible in everyday speech, they will realise need to be described as likely or unlikely, even if there is a very large or very small chance (respectively) of their occurrence. Some statements referring to themselves, their families and their lives may be “likely” for some and “unlikely” for others. Similarly, in comparing statements with each other, students will find that some may be able to be generalised, but many will need to be more carefully described in order to label them as certain, impossible, likely or unlikely.
Year 3: Chance experiments and variation in results
There are many everyday activities in which chance plays a part and in which chance and its effects often contribute to the interest of activities. In Year 3, students can conduct experiments in everyday activities that involve chance, describe possible outcomes, and see the effects of chance in the variation in observed outcomes.
Example A: “Bounce of the ball”
Because of the uncertainty involved in the bounce of a ball in many sports, particularly football, the phrase “bounce of the ball” is sometimes even used as a metaphor for events subject to chance. Usually it refers − whether in sport or metaphorically speaking − to direction of bounce, but conducting an experiment with balls that bounce in different directions might not be suitable for Year 3 students.
However, an experiment in which it is easier to describe and observe possible outcomes, is to drop a ball and count how many times it bounces. Different balls and/or different surfaces can be used by different groups of students, so that they can compare their observations across groups, but at this level, it is suggested that each group should use just one ball and one surface and try to keep the action of dropping the ball as consistent as possible. All the students in a group counting the bounces for each drop helps in recording accuracy as it is surprisingly easy to mis-count when watching a ball bounce. The possible values of the number of bounces can be any counting value from
0 upwards, although of course large values become less and less likely.
Students can observe that even though the same ball is dropped the same way onto the same surface, chance is involved and there is variation in the number of bounces. However they will also be able to see how their group of observations compares with other groups, both in typical values and in extent of variation for different balls dropped
on the same surface, or for different ball and surface combinations.
Example B: Stretch a snake and see where it breaks
Part of the pre-eating interest of a jelly snake often seems to be in stretching them. Designing experiments to observe how far they can stretch is surprisingly challenging and is appropriate for a data investigation at a much higher level, but seeing where they break can be fun, particularly as they tend to break just behind the head because there tends to be a narrower part there.
Students can be encouraged to discuss how to stretch the snake (whether lying flat or holding vertically, whether to hold one end steady and stretch the other or stretch both ends at once, and how to do it so that they are doing it the same way each time. Students can decide if they are interested in whether it breaks behind the head or not, or whether they want to describe more possibilities. They can then stretch a number of snakes to investigate if there is variation, and, if so, which outcomes, or types of outcomes, appear to be the more likely.
Example C: Paper planes
How a paper plane flies depends on its design, how it’s thrown, whether there’s any wind, whether there are obstacles, and so on. But for one design, and under the same conditions and the same person throwing it, chance will affect the result. Students could create their own paper plane(s), or use instructions such as at http://www.10paperairplanes.com/how-to-make-paper-airplanes/03-the-arrow.html
They could look at whether it glides or turns over as it flies, whether it tends to go straight or curve, whether it tends to land smoothly or tend to nosedive, and if it goes further than a selected distance such as 3 metres.
Example D: Using a spinner
Some games use spinners to give players their next moves. When spun around its pivot, the arrow of the spinner comes to rest on a segment of a circle. Usually the different segments are in different colours, so the basic events of a single spin are the colours used for the different segments. In the spinner pictured below, there are 4 colours. So the list of the possible outcomes of a single spin of the arrow is (orange, red, green, blue).
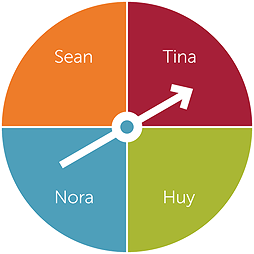
In Example C above, students could work in groups on either the design of the plane or throwing it and noting what happens or both. A spinner could be used to choose who takes different roles, such as the thrower, or which way the plane will be thrown, etc. The students do not need to recognise that the segments are equally-likely, and recognising that the segments are equally-likely is in the Year 5 curriculum, but they will see that chance is being used to choose roles or procedures.
Some general comments and links
towards years 4 and 5
From Years 1-3, students gradually develop understanding and familiarity with simple and familiar events involving chance, including possible outcomes. They move from considering events that “will”, “won’t” or “might” happen to considering whether they are “likely”or “unlikely” with some being “certain” or “impossible”. They create and conduct simple experiments using familiar and everyday fun activities involving chance, and describe possible outcomes of these. In carrying out these experiments, they see the effects of chance in the variation in the results. They do not need to compare or in any way quantify chance in order to recognise that chance results in variation. Nor do they need to use any presentation of their observations, as they can describe the variation they see in their own words and ways.
In Year 4, they consider more carefully how to describe possible outcomes of simple situations involving games of chance or familiar everyday outcomes. Without assigning any values for probabilities, they consider how the probabilities of possible outcomes could compare with each other. They also consider simple everyday events that cannot happen together and, in comparison, some that can. If events cannot both happen, then most definitely, if one happens there is no chance the other can. This helps students start to think about simple situations in which it is reasonable to assume that the occurrence of one event does not affect or change the chance of occurrence of another event.
In Year 5, consideration of the possible outcomes of simple situations leads to assigning equal probabilities in some of these, understanding what the values of these probabilities must be and representing these values using fractions.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
