The Improving Mathematics Education in Schools (TIMES) Project
It is assumed that in Years 1-8, students have had many learning experiences that consider simple and everyday events involving chance, and descriptions of them. They have considered which events are, or may be assumed, more or less likely, and, if events are not more or less likely than others, then they have considered that it is reasonable to assume the events to be equally-likely. They have looked at simple everyday events where one cannot happen if the other happens, and, in contrast, they have thought about simple situations where it is reasonable to assume that the chance of occurrence of an event is not changed by the occurrence of another. They recognise impossible and certain events, and that probabilities range from 0 to 1. They have listed outcomes of chance situations for which equally-likely outcomes may be assumed. They have represented probabilities using fractions, decimals and percentages. They have had hands-on, real and virtual learning experiences in how probabilities can affect observations in both small and larger amounts of data (real and virtual), and have compared observed frequencies with expected frequencies corresponding to given or assumed sets of probabilities. In everyday simple situations, with a clear and easily listed number of possible outcomes that can, or may, be assumed to be equally-likely, they have considered probabilities of events by applying the concept of equal chances for equal “sizes” of events, and have collected data to compare observed frequencies with expected frequencies in these situations. In Year 8, students have re-visited some of the properties of events and probabilities they have seen and been using in simple situations in previous years, and generalised them to summing probabilities of disjoint events, including the special case of complementary events. Students have described, interpreted and represented events in more general situations, using the language of “not”, “at least” and “and”, and learned of the ambiguities in the use of the word “or”.
Statistics and statistical thinking have become increasingly important in a society that relies more and more on information and calls for evidence. Hence the need to develop statistical skills and thinking across all levels of education has grown and is of core importance in a century which will place even greater demands on society for statistical capabilities throughout industry, government and education.
Statistics is the science of variation and uncertainty. Concepts of probability underpin all of statistics, from handling and exploring data to the most complex and sophisticated models of processes that involve randomness. Statistical methods for analysing data are used to evaluate information in situations involving variation and uncertainty, and probability plays a key role in that process. All statistical models of real data and real situations are based on probability models. Probability models are at the heart of statistical inference, in which we use data to draw conclusions about a general situation or population of which the data can be considered randomly representative.
Probability is a measure, like length or area or weight or height, but a measure of the likeliness or chance of possibilities in some situation. Probability is a relative measure; it is a measure of chance relative to the other possibilities of the situation. Therefore, it is very important to be clear about the situation being considered. Comparisons of probabilities − which are equal, which are not, how much bigger or smaller − are therefore also of interest in modelling chance.
Where do the values of probabilities come from? How can we “find” values? We can model them by considerations of the situation, using information, making assumptions and using probability rules. We can estimate them from data. Almost always we use a combination of assumptions, modelling, data and probability rules.
The concepts and tools of probability pervade analysis of data. Even the most basic exploration and informal analysis involves at least some modelling of the data, and models for data are based on probability. Any interpretation of data involves considerations of variation and therefore at least some concepts of probability.
Situations involving uncertainty or randomness include probability in their models, and analysis of models often leads to data investigations to estimate parts of the model, to check the suitability of the model, to adjust or change the model, and to use the model for predictions.
Thus chance and data are inextricably linked and integrated throughout statistics. However, even though considerations of probability pervade all of statistics, understanding the results of some areas of data analysis requires only basic concepts of probability. The objectives of the chance and probability strand of the F-10 curriculum are to provide a practical framework for experiential learning in foundational concepts of probability for life, for exploring and interpreting data, and for underpinning later developments in statistical thinking and methods, including models for probability and data.
In this module, in the context of understanding chance and its effects in everyday life, we consider situations involving two stages or two variables, so that events are described in terms of pairs of outcomes. These events can often be usefully represented by arrays of pairs of outcomes. Some of the situations that involve two clear stages or steps are special cases that are sometimes called two-step chance experiments, and some of these introduce the concept of the second stage or step occurring with or without replacement. These special cases are sometimes usefully represented by tree diagrams.
After considering and describing a variety of simple and everyday examples, we turn to assigning probabilities from assumptions or estimating probabilities using data. In the situations where probabilities are assigned from assumptions, we can use some of these assumptions and probabilities in determining probabilities of events involving “and” or “at least” or “not”. In the situations in which probabilities are estimated from data, we can estimate the probabilities of such events directly from data without making any assumptions.
Estimation of probabilities is the aim of official and large-scale surveys, and this module also considers an example of such a survey to demonstrate how estimation of means and medians in populations is essentially based on estimating probabilities.
Concepts, assumptions, representations and the language of events and probability are experienced through examples of situations familiar and accessible to Year 9 students and that build on concepts and experiences introduced in Years 1-8.
Chance situations involving two stages or two variables
There are many simple and everyday situations in which pairs of outcomes occur or are of interest. Sometimes such pairs may occur in terms of “first …, then …” and sometimes there may not be a natural distinction between what happens “first” and what happens “second”. As always in statistics, careful description of the situation and its events are necessary and important, as these provide the framework for identifying assumptions and assigning probabilities or for planning a data investigation to estimate probabilities.
Students have previously seen the special example of throwing two dice because of its simplicity and its familiarity in playing board and other games. Hence we start by re-visiting this example before continuing with a variety of simple and everyday examples involving two stages or two variables. Two-stage situations implicitly or explicitly involve two variables that describe the outcomes of each “stage”. In each example, the possible outcomes are carefully and fully described, and some are represented diagrammatically if this is useful.
Example A: Throwing two dice or throwing one die twice
If the single or pair of six-sided dice are each fair and they are well shaken in a container before throwing, there is no difference statistically between throwing two dice and throwing one die twice. The outcomes are all the ordered pairs of numbers from 1 to 6:
(1, 1), (1, 2), (2, 1), (1, 3), (3, 1), (1, 4), (4, 1), (1, 5), (5, 1), (1, 6), (6, 1), (2, 2), (2, 3), (3, 2), (2, 4), (4, 2), (2, 5), (5, 2),
(2, 6), (6, 2), (3, 3), (3, 4), (4, 3), (3, 5), (5, 3), (3, 6), (6, 3), (4, 4), (4, 5), (5, 4), (4, 6), (6, 4), (5, 5), (5, 6), (6, 5), (6, 6).
These can also be expressed by using “and”. For example, we can denote the first die by A and the second by B, with A1 meaning the first die gives a “1”. Hence (1, 1) = “A1 and B1”.
What if the dice are identical? From a statistical point of view, we must speak in terms of the first die and the second die; in reality, they will not be exactly identical even if there is very little to physically distinguish them.
Example B: What colour sweets did you get?
Suppose you have a small box of different coloured sweets, such as M&M’s or Smarties. You give two to your friend by shaking one out of the box onto your friend’s hand and then by shaking out a second sweet onto your friend’s hand. If the colours of sweets in the box are red, yellow, green, blue, then the possible outcomes are ordered pairs of colours: (R, R), (R, Y), (R, G), (R, B), (Y, Y), (Y, R), (Y, G), (Y, B), (G, G), (G, R), (G, Y), (G, B), (B, B), (B, R),(B, Y), (B, G).
As in Example A, we can also denote these using “and”. For example 1R could be used to denote that the first sweet is red, so (R, Y) is the event “1R and 2Y”.
What if there is only one blue sweet in the box? It will be impossible to get a (B, B) outcome. However, this will be taken care of in the assigning of probabilities because the probabilities will depend on the numbers of different coloured sweets in the box. The probabilities will also take account that this situation is what is called without replacement, because the first sweet is removed from the box and then the second sweet is “selected”. Hence the chances of the different colours in the second “shake” of the box are affected by the colour of the first sweet, even though all the colours may be possible for the second sweet.
Example C: Prizes in raffles
Raffles are usually run by people buying numbered (and sometimes coloured) tickets with the tickets being in two parts. The buyers keep one part and the other parts (we’ll call them the ticket stubs) are put into a container with someone picking out a ticket at random from the container. The outcomes of the draw are all the tickets that have been sold.
Usually there is more than 1 prize in a raffle, and often more than two, but we will consider just two prizes requiring two draws. Let’s consider that the first draw is for second prize and the second draw is for the major prize. The outcomes of the raffle draw(s) are all the ordered pairs of raffle tickets sold. These are far too numerous to list them all! If they are all of one colour and the tickets are sold in order of number (that is, the books of tickets are worked through in order), then we could describe the possible outcomes as all the pairs of numbers (i, j) where i can take any value from 1 up to the last ticket number sold, and j can take any of these numbers except i.
This is also an example of what is called selection without replacement, because if the first ticket drawn was replaced, the second prize winner has a non-zero chance of winning first prize!
Example D: Is there a car space?
Consider a car park with two levels. People drive through one level to get to the second. A possible signage system could distinguish the two levels and indicate if there is a space or not on each level. The outcomes can be written as (S, NS), (S, S), (NS, S), (NS, S) where the first letter in each pair refers to the first level and the second letter refers to the second level. S = at least 1 space available; NS = no spaces available. This can be easily represented by what is called a tree diagram, as below.
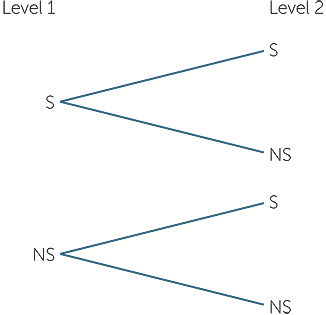
Another possible way of describing this situation is to give the actual number of spaces available on each level. The outcomes in this description would be ordered pairs of numbers, where the first number can go from 0 to the maximum number of spaces on level 1, and the second number can go from 0 to the maximum number of spaces on level 2. For example, if there are 50 spaces on each level, the outcomes if we give this full information of number of spaces on each level, would be all the ordered pairs (i, j) where each of i and j can take any values from 0 to 50.
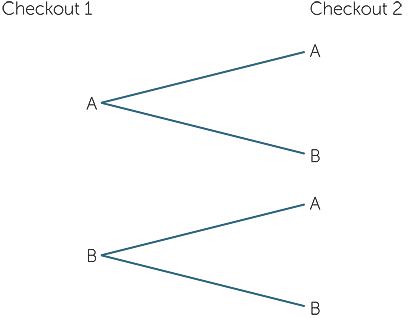
Example E: Which queue to choose?
Consider a supermarket which has two checkouts open for shoppers with under 12 items. We could describe this situation similarly to Example D. We could choose to classify the situation at each checkout by whether there’s 0 or 1 shopper at that checkout, or whether there’s more than 1. Notice that these include a shopper being served. Let’s denote by A the situation of 0 or 1 shoppers at a checkout, and by B the situation of more than 1. Then the possibilities are (A,A), (A,B), (B, A), (B, B). The event B is of course the complement of A; that is, not-A is the event “not at most 1 shopper” = “at least 2 shoppers”.
As in Example D, these can also be represented by a tree diagram.
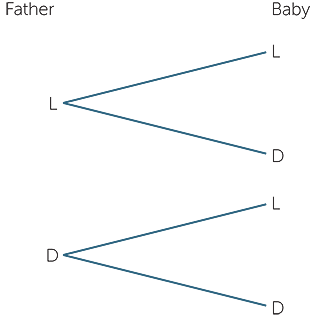
Example F: Does the baby have dark or light eyes?
It seems that people always ask about the eye colour of a baby and whether the baby has eye colour similar to the mother or father. There are many different ways we could describe eye colour but the two main classifications are light and dark. So to talk about, say, the father’s eye colour and the baby’s eye colour, we need pairs of descriptors − the first describing the father’s eye colour and the second describing the baby’s eye colour.
If we use just two descriptors of light and dark, we get the possibilities of (L, D), (L, L),
(D, L), (D, D).
As in all these examples, we can also denote these using “and”. For example, we can denote father’s eye colour light by FL, and baby’s eye colour light by BL, so that the event (L, L) can be denoted by “FL and BL”. Similarly the event (D, L) can be denoted by “FD and BL”.
As in Example D, these can also be represented by a tree diagram.
Alternatively, we might want better descriptors than that, and choose to classify eye colour as blue, green/grey/hazel, and brown/black. Let’s denote these by Bl, G, Br. Then a tree diagram looks like

Example G: Clasping hands and folding arms
When you clasp your hands, which thumb is on top? When you fold your arms, which arm is on top? Almost everyone finds that when they clasp their hands, the same thumb tends to be on top and it is very difficult to clasp such that the other thumb is on top. This observation, plus scientific articles such as the one at http://humangenetics.suite101.com/article.cfm/dominant_human_genetic_traits, do tend to indicate that it is a characteristic an individual is born with − a genetic trait. The article includes the following statement:
“Clasp your hands together (without thinking about it!). Most people place their left thumb on top of their right and this happens to be the dominant phenotype. Now, for fun, try clasping your hands so that the opposite thumb is on top. Feels strange and unnatural, doesn’t it?”
Folding arms has not received the same type of attention, possibly because it is easier to fold your arms differently to your usual way. But, similarly to clasping hands, people do tend to fold their arms the same way each time. For arm folding, we can just describe the outcome by which (fore) arm is on top, or we can distinguish further by whether one hand, no hands or both hands are showing. If we just look at which arm is on top, the outcomes are ordered pairs of L and R, with the first letter referring to the top thumb in clasping hands and the second letter referring to the top arm in folding arms: (L, L), (L, R), (R, L), (R, R).
If we record the hands in folding arms as well as the top arm, we would have 6 possibilities for the second variable, giving us possible outcomes of: (L, L0), (L, L1), (L, L2), (L, R0), (L, R1), (L, R2), (R, L0), (R, L1), (R, L2), (R, R0), (R, R1), (R, R2).
Again, as in previous examples, we can also denote these using “and”. For example, if we use the letter T to denote thumb and A to denote arm, then we can denote the outcome left thumb on top in clasping hands by TL, and left arm on top in folding arms with 1 hand showing, by the event “TL and AL1”.
Example H: Do people tend to underestimate or overestimate time?
How well do people estimate periods of time such as 5 seconds and 10 seconds. Is there a tendency to overestimate or underestimate? For an experiment in which people estimate 5 secs first and then 10 seconds, we could record the actual times they guessed, or simply record whether they underestimated or overestimated, giving us possible outcomes of: (U5, U10), (U5, O10), (O5, U10), (O5, O10) where, for example, U5 means an underestimate for 5 secs. If we decide that being out by less than 0.5 second is close enough to be regarded as correct, we would have 9 possible outcomes: (U5, U10), (U5, O10), (U5, C10), (O5, U10), (O5, C10), (O5, O10), (C5, U10), (C5, C10), (C5, O10).
The notation is thus already in place to denote events using “and”. For example, (U5, U10) = “U5 and U10”.
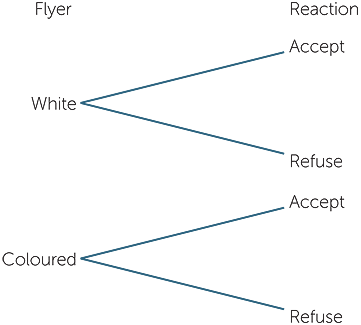
Example I: Do people tend to take coloured
or white flyers?
Flyers advertising events or publicising views are often offered to passersby on busy pedestrian ways. What makes people accept or refuse a flyer? Would coloured ones be more likely to be accepted? If a person handing out flyers had a mixture of white and coloured ones, we have a two-stage or two-variable situation with outcomes consisting of colour of flyer and whether the passerby offered the flyer accepts of does not accept it. This could be shown in a tree diagram as below:
Assigning and finding probabilities from assumptions
Probabilities can be assigned based on assumptions or based on estimation from data. Once probabilities are assigned, whether from assumptions or estimation or a combination, they obey the same rules. So far, the rules we have are that:
- the probability of a complement of an event is 1- the probability of the event;
- the probability of at least one of a number of disjoint events occurring is obtaining by summing the probabilities of the disjoint events;
- from this it also follows that for a list of equally-likely disjoint events, the probability of one of a number of them occurring is given by (number of possibilities of interest)/(total number of equally-likely events).
Example A: Throwing two dice or throwing one die twice
If the single or pair of six-sided dice are each fair and they are well shaken in a container before throwing, there is no difference statistically between throwing two dice and throwing one die twice, and the 36 ordered pairs of numbers can be assumed to be equally-likely.
The event of throwing a double is obtaining one of the 6 pairs of doubles. These are disjoint events, so the chance of throwing a double is 6/36. The event of obtaining a total of 4 is obtaining one of the 3 events (1,3), (2,2), (3,1), with probability therefore 3/36.
Example B: What colour sweets did you get?
Suppose you have a small box of 9 red, 6 green,10 yellow and 5 blue sweets. You shake a sweet onto your friend’s hand, and then another. If the box is well-mixed (e.g. shaken well) then the chance of obtaining a particular colour is (the number of the particular colour)/(total number of sweets in box). If two sweets are taken from a box, we need to consider the possible number of pairs of sweets. With 30 sweets in a box, there are 30 possible sweets for the first one shaken out, and for each of these there are a further 29 possible sweets left for the second one shaken out. So there are 30 × 29 possibilities in total for two sweets shaken out of the box. If the box is well-shaken, then we can assume all these possibilities are equally-likely. So the probability of getting a red and then a blue sweet is given by (the number of possible pairs with red first, blue second)/(30 × 29) = (9 × 6)/(30 × 29). The chance of getting two blue’s is (5 × 4)/(30 × 20).
Example C: Prizes in raffles
Raffles usually involve many tickets and very small chances of winning a prize, so we will consider a small raffle with only 100 tickets sold! As with Example C, there are 100 × 99 possible ordered pairs of tickets that can be selected in the draw, so the chance of you winning second prize (with your single ticket) and your mother winning first prize (again with just one single ticket) is 1/(100 × 99). If you buy 5 tickets in the raffle, the chance of your winning second prize but not first is (5 × 25)/(30 × 29) = 1/6 and the chance of your winning first prize but not second is (25 × 5)/(30 × 29) = 1/6 and the chance of you winning both first and second prizes is (5 × 4)/(30 × 29) = 2/87. So the chance of you winning at least one of first and second prizes = 1/6 + 1/6 + 2/87.
Estimating probabilities from data
Probabilities can be estimated from data by relative frequencies. Frequencies and relative frequencies are introduced and used extensively in the modules, Data investigation and interpretation modules, from Year 5 on.
Reminders:
Frequencies of categories or of count values are the numbers of observations in the data that fall into each category or that take each count value.
Relative frequencies of categories are the fractions or proportions of observations in the data that fall into each category.
Estimated probabilities can be assigned to events, and they obey the usual rules of probability. We can estimate events involving “at least”, “and” and “not” directly from data.
Example F: Does the baby have dark or light eyes?
The table below gives the frequencies of eye colours observed in a group of fathers
and children.
| Child’s Eye Colour | Father’s Eye Colour | ||
| Light | Dark | ||
| Light | 471 | 148 | 619 |
| Dark | 151 | 230 | 381 |
| 622 | 378 | 1000 | |
From these data, we can estimate the probabilities of:
- father’s eye colour light and child’s eye colour light
- father’s eye colour light and child’s eye colour dark
- father’s eye colour dark and child’s eye colour light
- at least one of father or child having light eye colour
- one of father and child having light eye colour but not both
- child having light eye colour
by
- 471/1000 = 0.471
- 151/1000 = 0.151
- 148/1000 = 0.148
- 0.471 + 0.151 + 0.148 = 0.77
- 0.151 + 0.148 = 0.299
- 619/1000 = 0.619
Example G: Clasping hands and folding arms
The table below gives the frequencies observed in a large group of 259 young people for the experiment of clasping hands and folding arms, with the notation , with the number after the letters in folding arms denoting the number of hands showing when the arms are folded (0, 1 or 2).
| Upper arm and number of hands showing in folding arms |
|||||||
| Upper thumb in clasping hands | AL0 | AL1 | AL2 | AR0 | AR1 | AR2 | Total |
| TL | 17 | 51 | 9 | 12 | 50 | 4 | 143 |
| TR | 16 | 37 | 8 | 13 | 36 | 6 | 116 |
| Total | 33 | 88 | 17 | 25 | 86 | 10 | 259 |
Based on these data, we can estimate probabilities using relative frequencies, and using “and”, and “or” for disjoint events. For example, we can estimate the probability of:
- i
- having the left thumb on top in clasping hands, by 143/259 = 0.552;
- ii
- having the left arm on top in folding arms = AL0 or AL1 or AL2, by 33/259 + 88/259 + 17/259 = 138/259 = 0.533;
- iii
- having the right arm on top in folding arms by 1 − 0.533 = 0.467;
- iv
- having no hands showing in folding arms = AL0 or AR0, by 33/259 + 25/259 = 58/259 = 0.224;
- v
- having the left thumb on top in clasping hands and the left arm on top in folding arms with 1 hand showing = (L, L1) = “TL and AL1”, by 51/259.
What are some of the questions that tend to arise in considering this experiment? Some are considered in Year 10 and the experiment is also considered in the modules, Data investigation and interpretation.
Example H: Do people tend to underestimate or overestimate time?
The table below gives the frequencies in a group of 120 people in a range of age groups, who were asked to estimate 5 seconds and then estimate 10 seconds, but without being told how accurate was their 5 second guess. The guesses were recorded in seconds, but the table presents the data in categories, classified by whether they underestimated (U) or overestimated (O) or were correct (C) to within 0.5 second.
| 10 second guess | ||||
| 5 second guess | C10 | O10 | U10 | Total |
| C5 | 21 | 9 | 19 | 49 |
| O5 | 4 | 6 | 4 | 14 |
| U5 | 9 | 5 | 43 | 57 |
| Total | 34 | 20 | 66 | 120 |
Based on these data, we can estimate probabilities using relative frequencies and also using “and”, and “or” for disjoint events. For example, we can estimate that a person:
- i
- estimates 5 seconds to within 0.5 second = C5, by 49/120 = 0.41;
- ii
- estimates 10 seconds to within 0.5 second = C10, by 34/120 = 0.283;
- iii
- estimates 5 seconds to within 0.5 second but underestimates 10 seconds = (C5, U10) = “C5 and U10”, by 19/120 = 0.158;
- iv
- estimates 5 seconds to within 0.5 second but does not estimate 10 seconds correctly = (C5, O10) or (C5, U10) = “C5 and O10” or “C5 and U10”, by 9/120 + 19/120 = 0.233.
An example in a large official survey
Surveys carried out by (or for) government departments and large companies and organisations either explicitly or implicitly estimate probabilities. If the survey is to gain information about a large population by survey sampling methods, then we usually say they are estimating population proportions rather than probabilities, but a population proportion does in fact give the probability of an event occurring, so such estimates are estimates of probabilities.
Example J: ABS survey on Children’s Participation in Cultural and Leisure Activities Survey
This survey (report 4901.0 on https://www.abs.gov.au/ausstats/abs@.nsf/mf/4901.0) is an extensive survey covering a wide range of activities. Many variables are considered. As with many public reports, various types of summaries are available but not necessarily the raw data. As with any quality reporting, the ABS always includes in their reports clear and detailed information as to how the data were collected, and what it consists of. One of the activities covered in the survey is reading for pleasure. The survey asks for the number of times an activity is engaged in (usually over a year) and the amount of time spent on the activity during the most recent two weeks. The report considers age groups and gender. In this module, we focus on the duration of the activity in the most recent two weeks (for each respondent) for reading for pleasure. These is in minutes. We see the types of information that are typically given or not given in public reports of this nature.
The following is an extract from the ABS report 4901.0 on the issue of time children spend reading for pleasure.
| Australian Bureau of Statistics | ||||
Apr 2006 Children’s Participation in Cultural and Leisure Activities, Australia |
||||
| CHILDREN WHO READ FOR PLEASURE, Duration in last two weeks |
||||
| AGE GROUP (YEARS) | ||||
| 5−8 | 9−11 | 12−14 | Total | |
| NUMBER(‘000) | ||||
| 2 hours or less | 206.9 | 134.8 | 112.3 | 453.9 |
| 3−4 hours | 150.1 | 103.8 | 106.1 | 360.0 |
| 5−9 hours | 268.2 | 207.2 | 160.6 | 636.0 |
| 10−19 hours | 125.9 | 142.0 | 153.0 | 420.9 |
| 20 hours or more | 20.4 | 37.2 | 55.7 | 113.3 |
| Total | 771.5 | 624.9 | 587.7 | 1984.0 |
We see that data on a pair of variables are reported in the form of a table, so we have frequencies of events similar to the previous examples, where the cells of the table give frequencies for events connected by “and”. So 206,900 children were in the 5-8 age group and reported reading for pleasure for 2 hours or less in the two weeks before the survey. Hence 206,900/1984,000 = 0.1 is an estimate of the proportion of children who are in the 5-8 age group and who read for pleasure for 2 hours a week or less. Is this the proportion we would like to estimate? We are more likely to be interested in focussing on the age groups separately and estimating proportions (probabilities) within each age group. For example, for children aged between 12 and 14, we can estimate the proportion who read for pleasure for 2 hours or less a fortnight by 112.3/587.7 = 0.19, which we would usually quote as a % as 19%. We will see more of these types of datasets in Chance in Year 10.
We can estimate the proportion of children over all the age groups (so 5-14) who read for pleasure for 10-19 hours in a fortnight by 420,900/1984,000 = 0.212. So the estimate from these data is that 21% of children (5-14 years) read for pleasure for between 10 and 19 hours a fortnight, or the probability that a child reads for pleasure for between 10 and 19 hours a fortnight, is estimated to be 0.212.
In the module, Data investigation and interpretation (Year 7), students have seen and calculated the averages and medians of data − what we call the sample mean and the sample median. The report from the ABS (report 4901.0 on https://www.abs.gov.au/ausstats/abs@.nsf/mf/4901.0) on the time children spend on various activities in a fortnight provides averages and medians. For children who read for pleasure, the report gives an average and a median amount of time in hours in a fortnight for different age groups. For the 12-14 year age group, the average is quoted as 8.5 hours and the median as 6 hours.
Can we get 8.5 hours from the above given data? To calculate an average time we need the times for all 587,700 children in the age group 12-14 who were surveyed, add up all the times they report and divide by 587,700. But in the report, the amount of time spent reading has been grouped − put into just 5 categories. The probabilities (or population proportions) we are estimating are of categories of times. These are intervals of time. Perhaps we can represent those intervals by their mid-point and say that the number of children in each category read for the value given by the mid-point.
If we do this we can calculate the following value which might approximate the average for all 587,700 children in this age group.
![]() (112.3 × 1 + 106.1 × 3.5 + 160.6 × 7 + 153.0 × 14.5 + 55.7 × 20)/587.7
(112.3 × 1 + 106.1 × 3.5 + 160.6 × 7 + 153.0 × 14.5 + 55.7 × 20)/587.7
![]() = 4940.35/587.7 = 8.4
= 4940.35/587.7 = 8.4
This is very close to the quoted average of 8.5 hours. Indeed, if we take the representative time of the last group as 21 hours rather than 20 hours, we get 8.5 hours.
If we look more closely at what we are doing, we start to see the concept of the parameter we are trying to estimate − how long we expect a child in the age group 12-14 to spend reading for pleasure in a fortnight. Because the above calculation is the sum of (representative time spent reading)x(estimate of probability a child spends this long reading for pleasure).
Thus estimates of probability are either aims in themselves in large surveys or they are behind other information quoted from surveys.
Some general comments and links
from F-8 and towards year 10
From Years F-8, students have gradually developed understanding and familiarity with simple and familiar events involving chance, including possible outcomes and whether they are “likely”, “unlikely” with some being “certain” or “impossible”. They have seen variation in results of simple chance experiments. They have considered how to describe possible outcomes of simple situations involving games of chance or familiar everyday outcomes, and simple everyday events that cannot happen together or, in comparison, some that can. Consideration of the possible outcomes and of the circumstances of simple situations has lead to careful description of the events and assumptions that permit assigning probabilities.
Students have assigned and used probabilities in terms of fractions, decimals and percentages and considered the implications of probabilities for observing data in situations involving chance. They have collected data and carried out simple simulations of data to observe the effects of chance in small and larger sets of data.
In special, limited situations with a clear and easily listed number of possible outcomes that can, or may, be assumed to be equally-likely, students have considered probabilities of events by applying the concept of equal chances for equal “sizes” of events, and have collected data to compare observed frequencies with expected frequencies under the assumption of equally-likely probabilities. Students have seen that these are a special case of finding probabilities of events by summing probabilities of the disjoint (or mutually exclusive) outcomes making up the event, including the special case of complementary events. Students have explored, understood and used the language of “not”, “and”, “at least” and “or” as connectors in describing events in terms of others.
In Year 9, students have considered situations involving two stages or two variables, including the special case of what are sometimes called two-step chance experiments. They have assigned probabilities based on assumptions, or estimated probabilities from data. Probabilities of events involving “and” or “or” have been determined from assumptions or estimated from data.
In Year 10, students consider situations involving two or three stages or two or three variables. In the special case of two or three step chance experiments, they assign probabilities to outcomes in situations involving selections either with or without replacement. They explore, understand and use the language of “if”, “given”, “of”, “knowing that” and estimate probabilities from data in simple everyday situations that illustrate this language. This also involves awareness of common mistakes in interpreting such language, and leads to investigation of the concept of independence.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()

