The Improving Mathematics Education in Schools (TIMES) Project
Year : 8
It is assumed that in Years 1-7, students have had many learning experiences that consider simple and everyday events involving chance, and descriptions of them. They have considered which events are, or may be assumed, more or less likely, and, if events are not more or less likely than others, then they have considered that it is reasonable to assume the events to be equally-likely. They have looked at simple everyday events where one cannot happen if the other happens, and, in contrast, they have thought about simple situations where it is reasonable to assume that the chance of occurrence of an event is not changed by the occurrence of another. They recognise impossible and certain events, and that probabilities range from 0 to 1. They have listed outcomes of chance situations for which equally-likely outcomes may be assumed. They have represented probabilities using fractions, decimals and percentages. They have had hands-on, real and virtual learning experiences in how probabilities can affect observations in both small and larger amounts of data (real and virtual), and have compared observed frequencies with expected frequencies corresponding to given or assumed sets of probabilities. In everyday simple situations, with a clear and easily listed number of possible outcomes that can, or may, be assumed to be equally-likely, they have considered probabilities of events by applying the concept of equal chances for equal “sizes” of events, some of which are obtained as the number of equally-likely outcomes/total number of equally-likely outcomes. Students have also collected data to compare observed frequencies with expected frequencies in these situations.
Statistics and statistical thinking have become increasingly important in a society that relies more and more on information and calls for evidence. Hence the need to develop statistical skills and thinking across all levels of education has grown and is of core importance in a century which will place even greater demands on society for statistical capabilities throughout industry, government and education.
Statistics is the science of variation and uncertainty. Concepts of probability underpin all of statistics, from handling and exploring data to the most complex and sophisticated models of processes that involve randomness. Statistical methods for analysing data are used to evaluate information in situations involving variation and uncertainty, and probability plays a key role in that process. All statistical models of real data and real situations are based on probability models. Probability models are at the heart of statistical inference, in which we use data to draw conclusions about a general situation or population of which the data can be considered randomly representative.
Probability is a measure, like length or area or weight or height, but a measure of the likeliness or chance of possibilities in some situation. Probability is a relative measure; it is a measure of chance relative to the other possibilities of the situation. Therefore, it is very important to be clear about the situation being considered. Comparisons of probabilities − which are equal, which are not, how much bigger or smaller − are therefore also of interest in modelling chance.
Where do the values of probabilities come from? How can we “find” values? We can model them by considerations of the situation, using information, making assumptions and using probability rules. We can estimate them from data. Almost always we use a combination of assumptions, modelling, data and probability rules.
The concepts and tools of probability pervade analysis of data. Even the most basic exploration and informal analysis involves at least some modelling of the data, and models for data are based on probability. Any interpretation of data involves considerations of variation and therefore at least some concepts of probability.
Situations involving uncertainty or randomness include probability in their models, and analysis of models often leads to data investigations to estimate parts of the model, to check the suitability of the model, to adjust or change the model, and to use the model for predictions.
Thus chance and data are inextricably linked and integrated throughout statistics. However, even though considerations of probability pervade all of statistics, understanding the results of some areas of data analysis requires only basic concepts of probability. The objectives of the chance and probability strand of the F-10 curriculum are to provide a practical framework for experiential learning in foundational concepts of probability for life, for exploring and interpreting data, and for underpinning later developments in statistical thinking and methods, including models for probability and data.
In this module, in the context of understanding chance and its effects in everyday life, we initially revisit the situations considered in Year 7 to understand that the probabilities of events in those situations were essentially obtained by adding equal probabilities. We then move to considering probabilities of complementary events, and continue on to revisit concepts introduced in Year 4, and identify these as the concepts of mutually exclusive or disjoint events. This leads to identification and application of a core property of probability: that the probability of at least one of disjoint events happening is obtained by summing the probabilities of the events.
This leads us to consider how to describe, interpret and represent events in more general situations. The language of “at least” and “and” are the building blocks. The ambiguity in the word “or” is examined in a variety of everyday phrases.
Thus this module revisits concepts and simple situations from earlier years to consolidate and extend them. It then focuses on the language of describing everyday events. The emphasis is on language but some diagrammatic representations are used to illustrate the language of describing events. The pros and cons of these representations are also discussed.
Concepts, assumptions, representations and the language of events and probability are experienced through examples of situations familiar and accessible to Year 8 students and that build on concepts and experiences introduced in Years 1-7.
Events consisting of a number of disjoint equally-likely outcomes
In Year 4, students have considered everyday events where one cannot happen if the other happens.
For example, if a die is thrown, only one face is uppermost, and if a 6 is the outcome then none of the other numbers can occur. If a spinner is spun, only one of the colours is possible as the outcome (with the proviso that we decide what to do if the spinner appears to land on a boundary line between two colours). If we shake one sweet from a box onto a friend’s hand, only one colour is possible. The number of children in a family must take one of the values, 0, 1, 2, etc. and if our bus is early then it’s not on time and it’s not late.
In Year 7, simple situations are considered in which a number of outcomes can be easily listed and can, or may, be assumed to be equally-likely. Students then consider events that consist of a number of these equally-likely outcomes, and assign probabilities according to the number of equally-likely outcomes possible for the event of interest.
In such a situation, the probability of each equally-likely outcome is 1/(total number of possible outcomes). So if we assign probabilities to events by
(number of outcomes possible in the event)/(total number of possible outcomes),
then we are summing the probabilities of all the possible equally-likely outcomes in the event of interest.
Similarly if we consider equally-likely areas, and assign probabilities by
(area for event)/(total area),
then we are summing the probabilities of all the possible equally-likely areas that make up the event of interest.
This reminds us that probability is a measure, and hence, like other measures such as length, weight, time, distance etc, the total measure of non-overlapping items is obtained by summing their individual measures.
Some examples are given below.
Example A: Throwing one die
If a 6-sided die is fair and is well shaken in some container before throwing it, we can assume equally-likely probabilities for the 6 face values. Hence each face value has a chance of 
of appearing on one throw of a die.
What is the chance of an odd number? An odd number is obtained if the die gives us a 1 or a 3 or a 5. There are 3 possibilities, so we argue that the assumption of equally-likely face values extends to assuming that probabilities are given by the relative number of outcomes. There are 3 odd numbers in a total of 6 face values (1 to 6), so the probability of an odd number is 
= 
.
What we are actually doing here is summing the probabilities of a 1, 3, 5, giving us 
+ 
+ 
= 
= 
. We get an odd number if we get a 1 or a 3 or a 5. They have no overlap − that is, if one of them happens then neither of the other two can − so we find the probability of 1 or 3 or 5 happening by adding up their probabilities.
Example B: Throwing two dice
If both six-sided dice are fair and they are well shaken in a container before throwing, there is no reason not to assume that each of the above 36 outcomes is equally-likely. So we would assume that all of the ordered pairs of numbers are equally-likely when we throw two fair, differently coloured dice − or fair dice which can be distinguished in some way.
So the chance of getting each pair as listed above is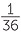 
. For example, the chance of getting two 6’s is 
.
Some board games use the sum of the faces of two dice to decide moves. What are the possible sums? Any of the numbers from 2 to 12 are possible. What is the chance of getting 12? It is the chance of getting two 6’s which is 
.
What is the chance of getting 11? There are two ways of getting 11; we could get a 5 on red & a 6 on blue or a 6 on red and a 5 on blue. These have no overlap, so we find the probability of (6, 5) or (5, 6) happening by adding their probabilities, giving us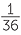 
+ 
= 
.
Similarly, the possible equally-likely outcomes to give a total of 10 are (4, 6), (5, 5), or (6, 4). There is no overlap in these − that is, if one happens then the others can’t − so the chance of getting a total of 10 is found by adding up the individual probabilities, giving us 
+ 
+ 
= 
.
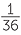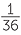Example C: What is the chance the winning ticket is one that you sold?
Raffles are usually run by people buying numbered (and sometimes coloured) tickets with the tickets being in two parts. The buyers keep one part and the other parts (we’ll call them the ticket stubs) are put into a container with someone picking out a ticket at random from the container. The outcomes of the draw are all the tickets that have been sold.
Often different coloured books of tickets are used, so that the winning ticket might be called out as “blue, number 16”. Suppose there are 5 ticket-sellers and each one has a book of 100 tickets and each book is a different colour. You are a seller and your book is green. All the tickets are sold. The stubs are put in a container and mixed well, and a guest pulls one out (without looking of course!). So there are 500 ticket stubs in the container and they are all equally-likely to be drawn. You sold 100 of these. So the chance of any one of the tickets you sold being selected is 
, and only one ticket can win. The chance that one of the 100 tickets you sold will be drawn is the sum over the 100 tickets of the chance of each of them winning. Summing 
100 times gives 
= 0.2 that the winning ticket will be one that you sold.
Example D: Which destination will the contestant win for a holiday?
In a TV contest, a contestant wins a holiday in Australia.
Suppose the contestant is blindfolded and places a pin on a board with Australian regions randomly placed on the map but with different areas of the board assigned to different regions, with no overlap of regions. If the regions and their areas on the board are as follows, what is the chance the contestant will win a holiday in Queensland?
Queensland: 12 cm2
NSW: 8 cm2
Vic: 4 cm2
SA: 8 cm2
WA: 16 cm2
Tas: 2 cm2
NT: 9 cm2
ACT: 1 cm2
The total area of the board is 60cm2. If you put a pin in a board at random, what will be equally-likely? All the regions with an area of 1cm2 will be equally-likely. Hence the chance of putting the pin into the region of the board representing Queensland is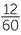 
= 
= 0.2. This is the same as obtaining the probability of getting 12cm2 is found by summing the probability of each of its component 1cm2 regions.
This then helps us see how to find the probability of winning the holiday in either Queensland or Victoria. The chance of winning it in Queensland is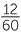 
and the chance for Victoria is 
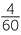. As the two regions do not overlap, the chance of winning the holiday in either Queensland or Victoria is the sum of these two, which is 
+ 
= 
= 
.
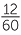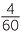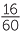The above examples are all of events where, if one happens, the other(s) cannot happen. They have no overlap. Such events are called disjoint or mutually exclusive events.
In all the examples above, the situations are of equally-likely outcomes, all disjoint by the very simplistic nature of the situations, and with probabilities of events found by summing these equal probabilities over the outcomes making up the event.
A special case of disjoint events takes us a step further in seeing how probabilities behave. If an event does NOT occur, we say that its complement has occurred. The complement of an event is the not-event, or the negation of the event, or the opposite of the event.
For example, if we do not get an odd number when we toss a die, we must get an even number. If the bus is not late, then it must be on time or early. If our team does not win, it either draws or loses. If the Australian holiday destination won by the contestant is not in Queensland or Victoria, it must be in NSW or South Australia or Tasmania or Western Australia or one of the territories.
If there are not at least 2 children in a family then there must be 0 or 1 child.
An event and its complement do not overlap and one of them has to happen − because the complement is anything that can happen other than the event of which it is complement. Hence the sum of their probabilities − no matter what they are − must be the probability of anything happening in the situation under consideration, and this must be = 1.
Hence the probability of an event NOT happening is 1 − the probability that it does happen.
Example A: Throwing one die
If a 6-sided die is fair and is well shaken in some container before throwing it, we can assume equally-likely probabilities for the 6 face values. Hence each face value has a chance of 
of appearing on one throw of a die.
The probability of an odd number occurring is the probability of getting a 1, 3, or 5, and hence is 
+ 
+ 
= 
= 
. If we do not get an odd number, we get an even number, so the probability of an even number is 1 − 
= 
.
Example B: Throwing two dice
If both six-sided dice are fair and they are well shaken in a container before throwing, there is no reason not to assume that each of the above 36 outcomes is equally-likely. So we would assume that all of the ordered pairs of numbers are equally-likely when we throw two fair, differently coloured dice − or fair dice which can be distinguished in some way.
The probability of getting a double is the probability of getting (1, 1) or (2, 2) or (3, 3) or
(4, 4) or (5, 5) or (6, 6). So this is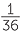 
+ 
+ 
+ 
+ 
+ 
= 
= 
.
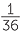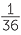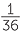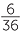Hence the probability of not getting a double is 1 − 
= 
.
Example C: What is the chance the winning ticket is not one that you sold?
Suppose there are 5 ticket-sellers and each one has a book of 100 tickets and each book is a different colour. You are a seller and your book is green. All the tickets are sold. The stubs are put in a container and mixed well, and a guest pulls one out (without looking of course!). So there are 500 ticket stubs in the container and they are all equally-likely to be drawn. You sold 100 of these. So the chance of any one of the tickets you sold being selected is 
, and only one ticket can win. The chance that one of the 100 tickets you sold will be drawn is the sum over the 100 tickets of the chance of each of them winning. Summing 
100 times gives 
= 0.2 that the winning ticket will be one that you sold. Hence the probability that the winning ticket is not sold by you is 1 − 0.2 = 0.8.
Example E: Will my bus be on time?
Your local council that runs the buses in your area prides itself on the punctuality of its buses and states that the buses run on time 90% of the time.
What do they mean by “on time”? It is most likely that they mean that it arrives either on time or early. What is the opposite of arriving on time or early? It is arriving late or not arriving at all. So if the council is correct, the probability of a bus arriving late or not at all is 1 − 0.9 = 0.1.
Example F: What is the probability that a family has only one child?
The phrase “an only child” is an everyday expression. Obtaining or estimating the probability of an “only child” is not simple and we will not attempt it here. Instead we will consider the complement. What is the opposite of a family having (exactly) one child? Shouldn’t it be that a family has 0 children or at least 2? Do you think this would be what people mean if they said that a family was not an “only child” family? If they mean the family has at least 2 children, then they are thinking of families with children − that is, having at least one child.
This illustrates that it is often useful to think of the complements of key events to make sure that the overall situation is clearly identified or defined.
If we are considering all families, whether they have children or not, then the complement of (exactly) one child is no children or at least two. If we are considering families with children (that is, with at least 1 child), then the opposite of 1 child is at least two children.
Example G: What is the probability a family has at least 1 child? At least 2 children?
The event of at least 1 child is made up of having 1 child, or 2 children or 3 children or 4 children, and so on. Even if we can find or estimate the probabilities of all these different numbers of children, we would have to sum a lot of probabilities. But using the complementary event will make this much easier, because the opposite of having at least 1 child is having no children. And the probability of at least 1 child = 1 − the probability of no children.
Similarly, finding the probability of at least two children by summing probabilities (of exactly 2 plus exactly 3 plus exactly 4 etc) is not going to be easy even if we know the probabilities (and are able to stop at some number of children!). Again it is usually easier to find the probability of at least two by working with the complement which is either none or 1. So the probability of at least two children = 1 − the probability of no children − the probability of exactly 1 child.
Example H: What is the probability the Australian cricket team will score more than 275 in a 1-day innings?
Such probabilities can only be estimated from data, but even when estimating from data, it may be easier to work with the complement. The complement of scoring more than 275 is scoring less than or equal to 275 runs, and the probability of scoring more than 275 = 1 − the probability of scoring less than or equal to 275.
Example I: Will both my buses will be on time?
Suppose I have to catch two buses to get to my destination, so I would like them both to be on time. What is the opposite of the event that both are on time (however this defined)? It’s not the event that both are not on time. If the event of both buses being on time does not happen, then it could be because of the first being on time but the other not, or the first not being on time but the other is, or that neither are on time.
Examples F and I illustrate how much care is needed with language in describing situations and events, and in interpretation of other people’s language. The next Section considers the everyday language that people use in describing events that involve two or more events in different ways.
The language of event “connectors”
The core word in considering a complementary event is “not”. An event and its complement are not so much connected by the word “not” as separated. In many cases, considering the opposite of an event defines its complement - defines the “not” of it.
Many events are constructed from other events by use of connecting words such as “or”, “and” and “at least”. These words are very common in everyday speech, but in considering events it is important to understand or identify exactly what is meant. And, as in describing situations and events, we need to identify exactly what is meant before thinking about probabilities.
The word “and” does not tend to cause many problems in its connection of events to form another as it is usually clear that both (or all) the events being connected by “and” must occur. In Example F above, the event of both buses being on time is the event “first bus is on time” and “second bus is on time”. This illustrates an alternative way of wording the connection “and” and the interpretation of its meaning − both of the connected events must happen.
The term “at least” also seldom has ambiguities. In the examples above, we see how often we are interested in the probability of at least When used as a connector of events, the expression is usually “at least one of …… occurs”. The issues with this tend to be that it should be used more than it is. Often in everyday speech, people mean “at least …” without clearly identifying this.
Example J: Do you mean exactly one or at least one?
This is the most common general situation that often requires clarification. If someone says “there’s a mistake on that page” do they mean exactly one mistake or at least one mistake? Usually they mean at least one mistake.
If someone says “I’m going into the city one day next week”, do they mean on exactly one day next week or at least one day next week? If someone says they think it’s going to rain one day next week, do they mean they think it’s going to rain on exactly one day or at least one day?
A prediction of a shower or two is a prediction of at least one shower.
If someone says they would like a sandwich, they might mean exactly one sandwich or at least one sandwich. But if someone says they are going shopping to buy a dishwasher, they almost certainly mean exactly one dishwasher!
The word “or” can be quite ambiguous, even though the context is sometimes of assistance. This is because “or” in everyday speech can be the exclusive “or” or the inclusive “or”. If it is used to connect disjoint events, it is naturally the exclusive “or” but this is because of the events it is connecting.
Thus, in Examples A to G above, the outcomes whose probabilities are being summed are disjoint and the events whose probabilities are being found (or are to be found) are connected by “or”.
For example, throwing an odd number on a die is throwing a 1 or a 3 or a 5. Throwing a double in throwing two dice is obtaining a pair of 1’s or a pair of 2’s or a pair of 3’s or of 4’s or of 5’s or of 6’s. A family with at least 1 child but no more than 6 has 1 or 2 or 3 or 4 or 5 or 6 children. A student gets an A or a B for an assignment because it’s not possible to get both simultaneously.
Here are some examples of everyday expressions involving the word “or” and clarification of the exact meanings − or the possible exact meanings.
Example K: The word “or”
“Does your family have a cat or dog?” This would tend to mean does your family have at least one of a cat or dog rather than does your family have a cat but not a dog or a dog but not a cat. That is, the “or” here is most likely an inclusive “or”.
“Are you going to the city on Saturday or Sunday?” The meaning of the word here may come from conversational emphasis. If the emphasis is on the word “or” then it may be intended to be the exclusive “or”. But if the emphasis is not on “or” then the question may simply be whether the person is going to the city on at least one of those days.
“There will be a shower or storm this afternoon”. Whether this is exclusive or inclusive use of “or” depends to some extent on one’s definition of “shower” and “storm” and again on the emphasis or not on the word “or”. Is a storm included in the word “shower”? Probably not − most people would keep their meanings separate. However, the word “or” here is most likely meant to be inclusive, and the sentence is saying that there will be at least one of a shower and a storm.
“Do you have an iPhone or a Blackberry?” It doesn’t matter whether it is unlikely that the questioner thinks the person questioned might have both or not; this is essentially an inclusive “or”. That is, “do you have at least one of an iPhone or a Blackberry?”
“There are one or two mistakes on that page”. This use of “or” is almost certainly inclusive, and the meaning is that there is at least one mistake on the page.
As the above examples illustrate, the inclusive “or” is best described in words by “at least”. It can also be expressed as “either… or….. or both”. The exclusive “or” needs to be expressed as “either….or……but not both”. A more exact but longer way of saying this is “either….but not ……, or …….. but not……..”. For example, “are you going to the city on Saturday but not Sunday, or on Sunday but not Saturday?”
Notice that this way of expressing the exclusive “or” can also involve complements, and can be expressed as “are you going to the city on Saturday and not on Sunday, or on Sunday and not on Saturday?” No wonder this is expressed in everyday conversation in a more abbreviated form, with the context and speech emphasis implying the meaning!
Similarly, the expression of the inclusive “or” as “either…or….or both” shows that it can be expressed in terms of the exclusive “or” plus “and”. For example, “are you going to the city on at least one of Saturday or Sunday?” can be expressed as “are you going to the city on Saturday but not Sunday or on Sunday but not Saturday or on both?” It is possible that this question may be the one the person wants to ask because they want one of the three potential responses.
Possible graphical representations
of “connectors” of events
The above dissection of “or” and “and” also leads into possible graphical representations of these connectors of events. Two possible representations are using a table or using a diagram called a Venn diagram. These are illustrated using one of the above examples.
Example L: Does your family have a cat or a dog?
| Cat | No cat | |
| Dog | Cat and dog | Dog but no cat |
| No dog | Cat but no dog | Neither dog nor cat |
“Cat and dog” are represented by just one cell in the table. The exclusive “or” is represented by two cells in the table, namely: “Dog but no cat” or “Cat but no dog”. Hence if either of these cells occurs then “cat or dog but not both” occurs. The inclusive “or” is represented by three cells of the table, namely “cat but not dog” or “dog but not cat” or “cat and dog”, and if any of these three cells occurs, then the event “at least one of cat or dog” occurs. It is almost always better to express the inclusive “or” in words by “at least”.
Note that the opposite of “cat and dog” is “at least one of cat or dog”.
Below is a Venn diagram which represents these events using regions.
In the above diagram, the areas of the regions have no meaning, but once probabilities are assigned, the areas could, if desired, be used to represent probabilities.
We see that “cat and dog” is more restrictive than “cat but no dog or dog but no cat” which is more restrictive than “at least one of cat or dog”. Alternatively, we can say that “at least one of cat or dog” has more possibilities in it than “cat but no dog or dog but no cat” which has more possibilities in it than “cat and dog”.
Some general comments and links
from F-8 and towards year 9
From Years 1-7, students have gradually developed understanding and familiarity with simple and familiar events involving chance, including possible outcomes and whether they are “likely”, “unlikely” with some being “certain” or “impossible”. They have seen variation in results of simple chance experiments. They have considered how to describe possible outcomes of simple situations involving games of chance or familiar everyday outcomes, and how the probabilities of possible outcomes could compare with each other. They have considered simple everyday events that cannot happen together and, in comparison, some that can. Consideration of the possible outcomes and of the circumstances of simple situations has lead to careful description of the events and assumptions that permit assigning probabilities.
Students have assigned and used probabilities in terms of fractions, decimals and percentages and considered the implications of probabilities for observing data in situations involving chance. They have collected data and carried out simple simulations of data to observe the effects of chance in small and larger sets of data.
In special, limited situations with a clear and easily listed number of possible outcomes that can, or may, be assumed to be equally-likely, students have considered probabilities of events by applying the concept of equal chances for equal “sizes” of events, and have collected data to compare observed frequencies with expected frequencies under the assumption of equally-likely probabilities.
In Year 8, students have seen that these are a special case of finding probabilities of events by summing probabilities of the disjoint (or mutually exclusive) outcomes making up the event. This has led to the concept of complementary events and their probabilities. Students have explored, understood and used the language of “not”, “and”, “at least” and “or” as connectors in describing events in terms of others. Although the emphasis is on the language, graphical representations of these in either tables or diagrams called Venn diagrams, can be of assistance in identification or clarification of expressions in words.
In Year 9, students build on these concepts to consider further situations involving two variables, including the special case of what are sometimes called two-step chance experiments. They identify assumptions and assign probabilities based on these assumptions, or estimate probabilities from data. These probabilities are then used to obtain probabilities of events involving “and” or “or”.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
