The Improving Mathematics Education in Schools (TIMES) Project
Year : 5
It is assumed that in Years 1-4, students have had many learning experiences that consider simple and familiar events involving chance, including describing possible everyday events and whether they are “likely”, “unlikely” with some being “certain” or “impossible”. In Year 4, they have considered which events are more or less likely, and, if events are not more or less likely than others, then they have considered that it is reasonable to assume the events to be equally-likely. They have looked at simple everyday events where one cannot happen if the other happens, and, in contrast, they have thought about simple situations where it is reasonable to assume that the chance of occurrence of an event is not changed by the occurrence of another.
Statistics and statistical thinking have become increasingly important in a society that relies more and more on information and calls for evidence. Hence the need to develop statistical skills and thinking across all levels of education has grown and is of core importance in a century which will place even greater demands on society for statistical capabilities throughout industry, government and education.
Statistics is the science of variation and uncertainty. Concepts of probability underpin all of statistics, from handling and exploring data to the most complex and sophisticated models of processes that involve randomness. Statistical methods for analysing data are used to evaluate information in situations involving variation and uncertainty, and probability plays a key role in that process. All statistical models of real data and real situations are based on probability models. Probability models are at the heart of statistical inference, in which we use data to draw conclusions about a general situation or population of which the data can be considered randomly representative.
Probability is a measure, like length or area or weight or height, but a measure of the likeliness or chance of possibilities in some situation. Probability is a relative measure; it is a measure of chance relative to the other possibilities of the situation. Therefore, it is very important to be clear about the situation being considered. Comparisons of probabilities − which are equal, which are not, how much bigger or smaller − are therefore also of interest in modelling chance.
Where do the values of probabilities come from? How can we “find” values? We can model them by considerations of the situation, using information, making assumptions and using probability rules. We can estimate them from data. Almost always we use a combination of assumptions, modelling, data and probability rules.
The concepts and tools of probability pervade analysis of data. Even the most basic exploration and informal analysis involves at least some modelling of the data, and models for data are based on probability. Any interpretation of data involves considerations of variation and therefore at least some concepts of probability.
Situations involving uncertainty or randomness include probability in their models, and analysis of models often leads to data investigations to estimate parts of the model, to check the suitability of the model, to adjust or change the model, and to use the model for predictions.
Thus chance and data are inextricably linked and integrated throughout statistics. However, even though considerations of probability pervade all of statistics, understanding the results of some areas of data analysis requires only basic concepts of probability. The objectives of the chance and probability strand of the F-10 curriculum are to provide a practical framework for experiential learning in foundational concepts of probability for life, for exploring and interpreting data, and for underpinning later developments in statistical thinking and methods, including models for probability and data.
In this module, in the context of understanding chance in everyday life, we build on the preliminary concepts of chance of Years 1-4 to focus more closely on describing possible events in simple and everyday situations in which it is reasonable to assign equal probabilities to outcomes.
Before probabilities can be assigned to any situation, it is necessary to understand that probabilities range from 0 to 1. Then for a (finite) number of equally-likely outcomes of a simple and everyday situation, we can assign the equal probabilities as fractions.
The emphasis is on carefully considering each situation and whether it is appropriate and sensible to assume equally-likely outcomes. The concepts are experienced through examples of situations familiar and accessible to Year 5 students and that build on concepts introduced in 1-4.
Before thinking about the chances of events, we need to identify and describe them clearly so that there is no confusion and anyone reading or hearing our description will be thinking of the events in the same way as us. Sometimes it is very easy to describe possible events and sometimes there is really only one way of describing them, but in many situations this is not so and careful description is therefore important.
No matter how complicated the situation, we will always be able to find a way of describing the events relating to it − indeed, we must. In many situations there may be slightly different ways of describing events, but in some simple and everyday situations there is an obvious and natural way of describing them. Usually in these types of very simple situations, we can also easily list these simple events.
We will consider situations in which the description of the events is straightforward and natural and easily listed. We start with very simple situations that are part of games of chance, and then consider some simple everyday events.
Events used for some games of chance
In many games, such as board games, moves are decided by the chance throws of dice or spins of spinners.
Example A: Throwing dice
Many board games use throws of one or two dice to give how many places to move or what choice is to be made. The usual single die has 6 sides, with each side having a number of marks giving its face value of one of the values 1, 2, 3, 4, 5 or 6. So the outcomes of a throw or toss of a single die are very simple to describe and there is really no other way of describing the outcome except as the face value of the uppermost face when the die lands, and hence the list of possible events is simply the set of numbers (1, 2, 3, 4, 5, 6).
Many board games use throws of two dice. Again it is simple to describe the basic outcomes of throws of a pair of dice, whether they are tossed together or one after the other. The basic events are pairs of numbers, where each number is the face value of the uppermost face of one of the dice. We will consider two different coloured dice or two dice that are marked in some way so that we can tell them apart. The list of possible outcomes is the list of pairs of numbers from 1 to 6, where the first number in each pair is the uppermost face of die 1 (for example, this might be a red die) and the second number in each pair is the uppermost face of die 2 (for example, this might be a blue die) as follows:
(1, 1), (1, 2), (2, 1), (1, 3), (3, 1), (1, 4), (4, 1), (1, 5), (5, 1), (1, 6), (6, 1), (2, 2), (2, 3), (3, 2), (2, 4), (4, 2), (2, 5), (5, 2), (2, 6), (6, 2), (3, 3), (3, 4), (4, 3), (3, 5), (5, 3), (3, 6), (6, 3), (4, 4), (4, 5), (5, 4), (4, 6), (6, 4), (5, 5), (5, 6), (6, 5), (6, 6).
Example B: Spinners
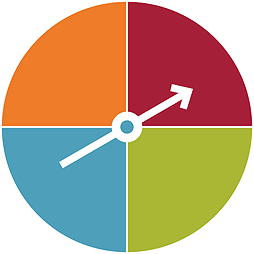
Some games, including board and other games, use spinners to give players their next moves. When spun around its pivot, the arrow of the spinner comes to rest on a segment of a circle. Usually the different segments are in different colours, so the basic events of a single spin are the colours used for the different segments. In the spinner pictured below, there are 4 colours. So the list of the possible outcomes of a single spin of the arrow is (orange, red, green, blue).
Below are some everyday situations for which it is easy to list the possible outcomes.
Example C: What colour sweet did you get?
Suppose you have a small box of different coloured sweets, such as M&M’s or Smarties. You give one to your friend by shaking one out of the box onto your friend’s hand. The possible events here are the possible colours of the sweet that lands in your friend’s hand. Whatever colours are possible for the sweets, then this is the list of possible outcomes. For example, the list of possible colours might be (red, yellow, green, blue, orange, brown).
Example D: Which colour firework goes the highest?
Some fireworks used in public fireworks displays send up coloured stars or flashes. One of this type is called the Roman candle. Commentators often like to ask crowds watching to guess which colour star will be next or which colour star will go the highest. If the possible colours for the stars of a Roman candle are red, blue, green, yellow, silver, then this list is the list of possible outcomes for the colour of the star that goes the highest.
Example E: Where does your newspaper land?
Many people living in towns or cities arrange for their newspaper to be delivered. Usually this is done by someone driving around the streets and throwing rolled and covered newspapers into the front of people’s places. A list of the possible landing places for the newspaper is (footpath but not the driveway, driveway on the footpath, driveway inside the boundary, grass inside the boundary, garden inside the boundary).
Example F: Which seedling will appear first?
We have planted 10 seeds in a planter box at the same time, and carefully watered them each day. Which seed will shoot first − that is, which of the 10 places in which we planted a seed, will we see the first showing of green?
Probabilities range from 0 to 1
Probability is a measure, like length or area or weight or height, but a measure of the likeliness or chance of possibilities in some situation. Like length or area or weight or height, probability cannot be below 0 − you can’t have less than no chance of something happening! Can probability be 0? Yes, if something is not possible at all, there is no chance it will happen. Its chance or probability of happening is 0. Notice that a very very very small chance of something happening is not a zero chance. There may be a very very very small chance that it will snow in Brisbane but it’s not absolutely 0.
Example C: What colour sweet did you get?
What is the chance you will shake out a blue sweet from your box onto your friend’s hand? Provided there are some blue sweets in the box, there is some chance a blue sweet will be shaken out. If there’s only 1 blue sweet and lots of others, there’s not much chance the blue will be shaken out, but there’s still some chance. But if there are no blue sweets at all in the box, then there’s no chance of a blue − it’s impossible to get a blue if there are no blues in the box. The probability of a blue one is zero.
Probability is a relative measure; it is a measure of chance relative to all the other possibilities of the situation. So we take all the probability and parcel it out amongst the various possibilities. Some get a bigger parcel of probability and some get a smaller parcel. How much is all the probability? It is 1. If something is certain to happen it has probability 1. So the whole probability for a particular situation is 1, and we divide this whole probability into probabilities that are smaller than one and share them around over the various possibilities.
Hence when we are describing a situation, we must make sure we cover all the possibilities. Otherwise we haven’t fully described the situation!
Example D: Which colour firework goes the highest?
Someone tells us that the possible colours for the stars of a Roman candle are red, blue, green, and yellow and we spread our total probability of one over those four colours in guessing which colour is going to shoot highest. And then during the firework display, a purple one shoots out. It had no probability assigned to it because the situation wasn’t completely described. We didn’t make a mistake; we just didn’t have full information.
Example E: Where does your newspaper land?
In the list of the possible landing places for the newspaper of (footpath but not the driveway, driveway on the footpath, driveway inside the boundary, grass inside the boundary, garden inside the boundary), have we considered all possibilities? We are assuming that the person throwing the newspaper will not miss our place altogether nor will they throw the paper in the gutter or on the road. Perhaps we should include these possibilities even if they have only a slight chance of happening. Otherwise we haven’t considered all possibilities. Alternatively, we could say that we are only considering the situation of the newspaper landing on the footpath or front area of our property, so that we are restricting the situation to that to exclude the possibility of it landing in the road, gutter or missing our place.
So probabilities for the possibilities of a situation are parts of the whole probability of 1. Probabilities are fractions of the whole probability of 1.
Equally-likely outcomes whose probabilities can be represented as fractions
We now consider assigning probabilities when we have a fixed number of possible outcomes and can consider that all our possible outcomes are equally-likely.
Events used for some games of chance
Example A: Throwing one die
In throwing one die, there are 6 possible outcomes. Are any of the faces more likely to come up than any others? A fair die is one for which it is assumed that the 6 faces are equally-likely to be uppermost in a toss of the die. If one or more faces are more likely to come up than others, the die is called a “loaded” die.
If we assume a die is fair, we have 6 possible outcomes all with the same chance of occurring. So we need to divide our total probability of 1 into 6 equal bits of probability. Therefore each bit of probability is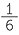 
.
Example B: Spinners
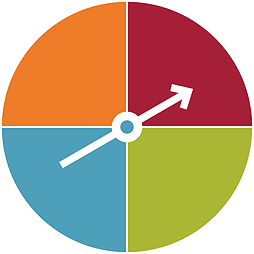
In the spinner pictured below, there are 4 colours, with the list of the possible outcomes of a single spin of the arrow is (orange, red, green, blue). The circle has been divided into 4 equal parts. First we need to decide what to do if the arrow appears to land on one of the dividing lines. [Note that this is caused by the fact that real lines do occupy a small amount of area as does the point at the head of the arrow. It is not possible to draw a real line that has no width!] In some games that use a spinner, if the arrow appears to fall on a line, the spin is taken again. Another possibility is to say that if the arrow appears to fall on a line, take it as falling on the colour to the left of the line. For either of these procedures, there are 4 possible outcomes of a spin, namely, orange, red, green, blue. If the arrow spins smoothly and if the spin is well done so that the arrow spins sufficiently thoroughly that it “forgets” its starting point, then each of the colours is equally likely to be the outcome. So the total probability of 1 is divided into 4 equal bits of probability. Each of these therefore is 
.
We now consider assigning probabilities when we have a fixed number of possible outcomes for a simple everyday situation and could consider under certain conditions that all our possible outcomes are equally-likely.
Example C: What colour sweet will you get?
In giving a sweet to your friend by shaking one out of your box of sweets onto your friend’s hand, suppose you have put sweets from a larger container into your small box, and you chose to put in 8 red, 8 yellow, 8 brown, 8 green and 8 blue and shaken the box well. The possible colours of the sweet you shake from the box into your friend’s hand are these 5 colours. If the box is well shaken, then none of these colours is more likely than the other. So the total probability of 1 is divided into 5 equal bits of probability. There is a chance of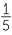 
that your friend will get any of the 5 colours.
Example D: Which colour firework goes the highest?
If the only possible colours for the stars of a Roman candle are red, blue, green, yellow, silver, then this list is the list of possible outcomes for the colour of the star that goes the highest. What do we need to know or assume, to be able to say that the highest star is equally-likely to be any of those 5 colours? Of course there must be at least one of each of the colours in the firework, but do we need to have equal number of the colours in the firework? Although it is not completely clear how this affects the chances of the highest colour, the assumption of equal numbers of stars in each colour does tend to make it more believable that the highest star is equally likely to be any colour because then we are just saying that the heights of the stars are random and are not affected by any of the other stars.
Example E: Where does your newspaper land?
If we assume that the person throwing the newspaper is good enough not to miss our place completely and to avoid it landing in the gutter or on the road, then the list of the possible landing places for the newspaper is (footpath but not the driveway, driveway on the footpath, driveway inside the boundary, grass inside the boundary, garden inside the boundary). What would we need to assume for these 5 areas to be equally-likely places for the newspaper to land? We can either assume directly that the thrower is equally-likely to get any of those places, or we can think of it like the spinner. If the areas of those 5 places are equal and if the delivery person throws at random over those 5 places then we can assume they are equally-likely. But is this sensible? We are saying that the thrower won’t miss those 5 places, but the throw is random within that restriction? There is nothing wrong with saying that this is what we are assuming, as long as we do say it clearly.
Example F: Which seedling will appear first?
We have planted 10 seeds at regular places (perhaps using a tray with 10 separate small compartments) in a planter box at the same time, and carefully watered them each day. Which seed will shoot first − that is, which of the 10 places in which we planted a seed, will we see the first showing of green? Can we assume each place is equally-likely to have the first shoot? Provided the conditions are the same over the 10 places, this is a reasonable assumption. We would need to be careful to make the conditions the same, for example, by making sure all the positions had the same amount of water and light. If we assume this, then the total probability of 1 is divided into 10 equal bits of probability, so that each place has a probability of 
to have the first shoot of green appearing.
An extension to events used for some games of chance
Example A: Throwing two dice
Many board games use throws of two dice. Again it is simple to describe the basic outcomes of throws of a pair of dice, whether they are tossed together or one after the other. The basic events are pairs of numbers, where each number is the face value of the uppermost face of one of the dice. We will consider two different coloured dice or two dice that are marked in some way so that we can tell them apart. The list of possible outcomes is the list of pairs of numbers from 1 to 6, where the first number in each pair is the uppermost face of die 1 (for example, this might be a red die) and the second number in each pair is the uppermost face of die 2 (for example, this might be a blue die) as follows:
(1, 1), (1, 2), (2, 1), (1, 3), (3, 1), (1, 4), (4, 1), (1, 5), (5, 1), (1, 6), (6, 1), (2, 2), (2, 3), (3, 2), (2, 4), (4, 2), (2, 5), (5, 2), (2, 6), (6, 2), (3, 3), (3, 4), (4, 3), (3, 5), (5, 3), (3, 6), (6, 3), (4, 4), (4, 5), (5, 4), (4, 6), (6, 4), (5, 5), (5, 6), (6, 5), (6, 6).
There are 36 of these possible pairs. Can we assume they are equally-likely? If the dice are fair and they are tossed at random and there is nothing to connect the tosses of each, then there is no reason to assume that any pair of faces is more likely than any other pair. So under these conditions, each of the 36 possible outcomes is equally-likely. The total probability of 1 is divided into 36 equal bits of probability, each being 
. That is, the probability of any of the above pairs of numbers, with the first number referring to the first die and the second number to the second die, is 
.
In each of the above examples, we have been able to describe the possible outcomes of a situation in terms of a complete list of outcomes, and been able to identify circumstances under which it is reasonable to assume that none of these outcomes are more or less likely than the others, that is, that all of these outcomes are equally-likely. Under these carefully described circumstances and assumptions, the probability of each of the list of outcomes is 1/(total number of outcomes in the list). Note this only applies not only when we can consider events as equally-likely but also when we can give a complete list the outcomes, of which there are a fixed and known total number.
Some general comments and links
from F-4 and towards year 6
From Years 1-4, students have gradually developed understanding and familiarity with simple and familiar events involving chance, including possible outcomes and whether they are “likely”, “unlikely” with some being “certain” or “impossible”. They have seen variation in results of simple chance experiments. In Year 4, they have considered more carefully how to describe possible outcomes of simple situations involving games of chance or familiar everyday outcomes, and, without assigning any values for probabilities, how the probabilities of possible outcomes could compare with each other. They have also considered simple everyday events that cannot happen together and, in comparison, some that can. In Year 5, consideration of the possible outcomes and of the circumstances of simple situations has lead to careful description of the outcomes and assumptions that permit assigning equal probabilities, understanding what the values of these probabilities must be and representing these values using fractions.
In Year 6, decimals and percentages are used along with fractions to describe probabilities. Understanding of probability is extended to considering the implications for observing data in situations involving chance. Each time we observe the situation, only one possible outcome can be observed. The values of probabilities tell us the chance of observing each outcome each time we take an observation, but what can we expect to see in a set of observations? How will real observations compare with what we expect to see?
Appendix Note for teachers’ background information
Much is written in educational literature about coin tosses and much has been tried to be researched and analysed in students’ thinking about coin tossing. This situation is far more difficult than is usually assumed in such research which often tends to take the assumptions of fair coins and independent tosses as absolutely immutable and not to be questioned. In addition a common mistake is to state that it demonstrates either poor or, in contradiction, good thinking, to say that a particular sequence of coin tosses with a mixture of heads and tails is more likely than a sequence of the same outcome, when in practice it is not made clear whether the researcher or the student is thinking of a particular ordered sequence or merely a mixture of heads and tails. For example, if a coin is fair and tosses are independent, the chance of HTHHTT is EXACTLY the same as the chance of HHHHHH, but many people think of the first outcome in terms of getting 3 H’s and 3 T’s which is not the same as getting a particular sequence with 3 H’s and 3 T’s.
With regard to the assumption of a fair coin and independent tosses, the assumptions are the same as tossing dice. However, it is more difficult in practice to toss a coin completely randomly than to toss dice randomly, and also to assume that a particular person does not tend to toss a coin in a similar manner each toss. It is also extremely difficult in practice to identify whether unlikely sequences are due to an unfair coin or how it is tossed, and it would be of far greater benefit in research, but far more challenging, to devise experiments in which these two assumptions could be separately investigated.
Indeed, if, on observing an unlikely sequence, students do question either the fairness of a coin or no connection between consecutive coin tosses, then are they not demonstrating intuitive understanding of statistical hypothesis testing? Note that there is a difference between observing a simulation and observing a real situation because assumptions are easier to accept in a simulation.
For some excellent comments on this, see the letter by Harvey Goldstein to the Editor of Teaching Statistics (2010), Volume 32, number 3. To see an example of contradictions in research approaches that take the assumptions of fair coin and independent tosses as absolute and not-to-be questioned, contrasted with use of observed sequences as learning experiences for statistical hypothesis testing, compare Ridgway and Ridgway (2010), Teaching Statistics Vol 32, number 2, p34, with Holland (2007), Teaching Statistics Vol 29, number 3, p71.
Because of the over-emphasis in educational research on coin tossing, and the problems caused by lack of clarity and understanding in much written on this topic, examples using coin tossing are avoided as much as possible in these modules.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
