The Improving Mathematics Education in Schools (TIMES) Project
It is assumed that in Years 1-3, students have had many learning experiences that consider simple and familiar events involving chance, including describing possible outcomes and whether they are “likely”, “unlikely” with some being “certain” or “impossible”.
Statistics and statistical thinking have become increasingly important in a society that relies more and more on information and calls for evidence. Hence the need to develop statistical skills and thinking across all levels of education has grown and is of core importance in a century which will place even greater demands on society for statistical capabilities throughout industry, government and education.
Statistics is the science of variation and uncertainty. Concepts of probability underpin all of statistics, from handling and exploring data to the most complex and sophisticated models of processes that involve randomness. Statistical methods for analysing data are used to evaluate information in situations involving variation and uncertainty, and probability plays a key role in that process. All statistical models of real data and real situations are based on probability models. Probability models are at the heart of statistical inference, in which we use data to draw conclusions about a general situation or population of which the data can be considered randomly representative.
Probability is a measure, like length or area or weight or height, but a measure of the likeliness or chance of possibilities in some situation. Probability is a relative measure; it is a measure of chance relative to the other possibilities of the situation. Therefore, it is very important to be clear about the situation being considered. Comparisons of probabilities − which are equal, which are not, how much bigger or smaller − are therefore also of interest in modelling chance.
Where do the values of probabilities come from? How can we “find” values? We can model them by considerations of the situation, using information, making assumptions and using probability rules. We can estimate them from data. Almost always we use a combination of assumptions, modelling, data and probability rules.
The concepts and tools of probability pervade analysis of data. Even the most basic exploration and informal analysis involves at least some modelling of the data, and models for data are based on probability. Any interpretation of data involves considerations of variation and therefore at least some concepts of probability.
Situations involving uncertainty or randomness include probability in their models, and analysis of models often leads to data investigations to estimate parts of the model, to check the suitability of the model, to adjust or change the model, and to use the model for predictions.
Thus chance and data are inextricably linked and integrated throughout statistics. However, even though considerations of probability pervade all of statistics, understanding the results of some areas of data analysis requires only basic concepts of probability. The objectives of the chance and probability strand of the F-10 curriculum are to provide a practical framework for experiential learning in foundational concepts of probability for life, for exploring and interpreting data, and for underpinning later developments in statistical thinking and methods, including models for probability and data.
In this module, in the context of understanding chance in everyday life, we build on the preliminary concepts of chance of Years 1-3 to focus more closely on describing possible events in everyday situations, and comparing their chances of occurring but without assigning any values to such chances.
In describing possible events, we also identify everyday events where one cannot happen if the other happens, and, for contrast, everyday events where it is possible that two might both occur.
Where two events cannot both occur at once, the chance of one occurrence is completely affected by the occurrence of the other − there is no chance! Hence starting to consider the nature of everyday events also leads us to questions about other simple everyday events. Do we think the chance of one occurring will or will not be affected by the occurrence of another? Are there simple everyday situations in which we are prepared to assume that the chance of one occurring will not be affected by the occurrence of another?
The concepts are experienced through examples that consider situations familiar and accessible to Year 4 students and build on concepts introduced in 1-3.
Before thinking about the chances of events, we need to identify and describe them clearly so that there is no confusion and anyone reading or hearing our description will be thinking of the events in the same way as us. Sometimes it is very easy to describe possible events and sometimes there is really only one way of describing them, but in many situations this is not so and careful description is therefore important.
Just thinking about how to describe weather shows how difficult it can be to describe some everyday events so that everyone knows what is meant. For example, if we say today is fine, do we mean sunny? Or do we mean no rain at all? When we say it rained today, do we mean at least some water fell, no matter how little? Or do we mean there was at least enough water fell to wet someone standing outside when it fell? Or do we mean rain fell for at least a certain amount of time during the day? Or do we mean at least a certain amount of rain fell? When we say it rained in Sydney, do we mean it rained for at least a certain amount (of time or rain) everywhere in Sydney? Or that it rained in at least one part of Sydney?
The weather − especially rain! − is far too difficult. So we will consider simpler situations, starting with very simple situations that are part of games of chance, and then consider some simple everyday events.
Events used for some games of chance
In many games, such as board games, moves are decided by the chance throws of dice or spins of spinners.
Example A: Throwing dice
Many board games use throws of one or two dice to give how many places to move or what choice is to be made. The usual single die has 6 sides, with each side having a number of marks giving its face value of one of the values 1, 2, 3, 4, 5 or 6. So the outcomes of a throw or toss of a single die are very simple to describe and there is really no other way of describing the outcome as the face value of the uppermost face when the die lands, and hence the possible events as the set of numbers 1,…6. In some games what matters is whether the uppermost face has an even or odd value, but these are just groupings of the basic events.
Many board games use throws of two dice. Again it is simple to describe the basic outcomes of throws of a pair of dice, whether they are tossed together or one after the other. The basic events are pairs of numbers, where each number is the face value of the uppermost face of one of the dice. If the dice are different colours, for example red and blue, then the basic events are the pairs of numbers 1 on red, 1 on blue; 1 on red, 2 on blue; 2 on red, 1 on blue; etc. If the dice look exactly the same, then the basic events are 1’s on both; 1 on one and 2 on the other; 1 on one and 3 on the other; 2 on both; etc. Many board games only use the sum of the uppermost face values from throwing a pair of dice. Again there is no difficulty in describing the possible events and they are made up of groups of the basic events, whether the dice are different or identical.
Example B: Spinners
Some games, including board and other games, use spinners to give players their next moves. When spun around its pivot, the arrow of the spinner comes to rest on a segment of a circle. Usually the different segments are in different colours, so the basic events of a single spin are the colours used for the different segments.
Below are some everyday situations and aspects of them in which it is fairly easy to describe the possible events.
Example C: What colour sweet did you get?
Suppose you have a small box of different coloured sweets, such as M&M’s or Smarties. You give one to your friend by shaking one out of the box onto your friend’s hand. The possible events here are the possible colours of the sweet that lands in your friend’s hand.
Example D: Which type of muffin is first to be finished?
Your teacher organises a muffin morning tea for which half a dozen muffins of each of 7 types (e.g. chocolate, berry, white chocolate, vanilla, butterscotch, apple, cinnamon). The possible events for the type of muffin that is finished first are these 7 flavours.
Example E: Where does your newspaper land?
Many people living in towns or cities arrange for their newspaper to be delivered. Usually this is done by someone driving around the streets and throwing rolled and covered newspapers into the front of people’s places. What are the possible landing places for the newspaper? We could describe these as simply on the footpath or inside the property, or we could describe the possible landing places as footpath, road, driveway, lawn, garden. Some students might wish to distinguish between roadway and gutter. Notice also that driveways go over footpaths, so we would need to be clear in our description of landing place.
Example F: How many children in a family?
What are the possible numbers of children in a family? 0, 1, 2, 3, ……. This might seem simple at first but there are some aspects that need clarification. Are we considering families with at least one child? What do we mean by a family? How do we allow for half-siblings and step-siblings? This is an everyday situation that seems very simple on the surface but needs a lot of discussion and careful description. Would it be easier to describe number of children living in a household?
Example G: How late is my bus?
Some bus stops have designated arrival times in timetables and, of course, buses that travel between towns or localities have identified arrival times. We can measure how late a bus is in arriving by the length of time in minutes it actually arrives after its designated arrival time. So what do people mean when they say their bus was late? They usually do not mean that the bus arrived at any time after its designated time. We could decide that we would describe a bus as arriving late if it arrived more than 5 minutes after its designated arrival time, and very late if it arrived more than 10 minutes after its arrival time. But notice that this would not be especially relevant if the bus had come from a long distance. If we are considering the situation of the bus’ arrival, we would also need to consider early and on time arrivals, and again would need to decide what we mean by on time. Do we need to allow for the possibility of the bus not arriving at all? If not, we need to say that we are considering the possibilities for time of arrival of the bus, assuming it does arrive.
Which events are more likely to occur?
We cannot measure probability the way we can measure length, weight or time. We choose or assign probabilities. In doing so, we consider carefully the nature of the situation, and use any information we might have, including information from data. But whatever knowledge about the situation or information from data that we might have, we are ALWAYS making assumptions when we choose or assign probabilities. Some of the fundamental questions that we might consider before assigning or choosing probabilities are which events could be assumed to be equally likely? Which events could be assumed to be more likely than others?
These questions are considered for the examples above.
Events used for some games of chance
In many games, such as board games, moves are decided by the chance throws of dice or spins of spinners.
Example A: Throwing dice
In throwing one die, there are 6 possible outcomes. Are any of the faces more likely to come up than any others? A fair die is one for which it is assumed that the 6 faces are equally-likely to be uppermost in a toss of the die. If one or more faces are more likely to come up than others, the die is called a “loaded” die.
We can’t ever be sure that a die is completely fair. We can assume a die is fair. We could conduct a data investigation to investigate if a die is fair.
Many games use tossing a pair of dice. The possible events when a pair of dice are tossed are the pairs of numbers that are on the uppermost faces. If both dice are fair, do we think any pairs of numbers are more likely than others? The situation is easier to consider when the two dice are different colours, so we will just consider the simple case of having a red die and a blue die and that they are both fair. Do we think that all possible pairs of numbers are equally-likely? If we do, are we making any more assumptions?
Example B: Spinners
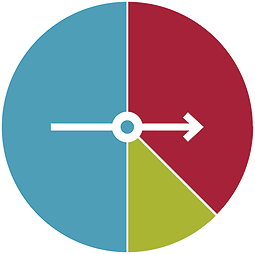
If a spinner is well-constructed so that the arrow spins smoothly around its centre, what will affect the colour or part of the spinner board on which it lands in a single spin? Suppose we have the spinner in the picture below and the arrow spins smoothly. Which colour do you think the arrow is most likely to land on? Which do you think is least likely?
If we think blue is most likely, and green is least likely, then we need to ask ourselves why we think this. We are saying that the bigger the section of colour, then the more likely is the spinner to land on it. We are saying that when the spinner spins smoothly, and is spun sufficiently that it doesn’t matter where the spinner started, then the larger portions of card are more likely than the smaller portions.
We now consider the possibilities of some simple everyday situations as described in the above examples.
Example C: What colour sweet is most likely?
Suppose you have a small box of different coloured sweets, such as M&M’s or Smarties. You give one to your friend by shaking one out of the box onto your friend’s hand. Of the possible colours, which is your friend most likely to get?
Suppose you have previously tipped the sweets out and know that there are 9 red, 8 yellow, 5 brown, 5 purple and 2 blue. You put the sweets back in the box, shake the, and tip one out. Which colour do you think it is most likely to be? If you think red, this is because you are thinking that there are most reds so there’s a greater chance of getting a red. Notice that − as you will know from doing this! − it won’t necessarily be a red − it’s just that there’s more chance of getting a red because there are more of them.
What’s the next most likely? Using the same assumption, it would be yellow. Brown and purple would be next and they’d be equally-likely. Blue is the least likely because there are only 2 blues.
Example D: Which type of muffin is most likely to be first to be finished?
Which of 7 types of muffins is most likely to run out of first? The most popular one! But how do we know which is most popular? We would need to collect data to get some information on popularity of types of muffins. We could do a survey amongst school students or perhaps ask a muffin shop. But we need to remember that a muffin shop would be giving answers for all their customers, and general favourite types of muffins might not be quite the same as those for Year 4 students.
Example E: What is the most likely place to find your newspaper in the morning?
To consider where the newspaper might land requires thinking not only of the possibilities and how large the various areas are, but also about what’s easiest for the driver throwing the paper, and whether he or she is trying to throw it somewhere in particular, such as the driveway. Even if we decide the driver doesn’t try to land it on a particular type of area, it is more likely to land at distances or on areas where it is easier to throw. So if a house has a large expanse of driveway, some lawn and very little garden area at the front of the house, then it is a reasonable assumption that the driveway is the most likely landing place, with the lawn second. But this will also depend on the throwing style of the paper deliverer, and possibly also on the type of road.
Example F: How many children in a family?
What can we say about which are more likely of the possible numbers of children in a family? There are more likely to be 2 or 3 than 6, and the chance of 10 or more would be small, but we cannot say much more than vague statements like that without information − information from data.
Example G: How late is my bus?
Buses are required not to leave certain bus stops before the times given on the timetable, so generally speaking, buses are more likely to be late than early. We are probably fairly safe to say that being up to 5 minutes late is more likely than being more than 5 minutes late. But, as in Example F, there is little more we can say about chances in this situation without information from observations and data. .
Which events cannot happen together? For which events
is there a chance they will happen together?
To see which events can or cannot happen together requires only consideration of the events themselves; that is, probabilities do not need to be considered. When we are describing possible everyday events, we do not have to describe them so that they cannot happen together, although it can often be convenient to do this. Sometimes, if enough care has not been taken in the description of possible events, some unintentional overlap in the description of possible events might cause some confusion.
The above examples are now considered to see which events cannot happen if others do.
Events used for some games of chance
Example A: Throwing dice
In the toss of one die, clearly only one face can be uppermost. So only one of the numbers 1, 2,..,6 can occur. If one of these numbers occur in tossing a die, none of the others can.
Example B: Spinners
A spinner works by dividing up the circle into segments. There is no overlap of segments so the arrow can point to only one segment for a single spin. If red is the outcome of the spin, no other colour can occur. Indeed, the spinner is designed for games so that the outcome of a spin gives one and only one result. Unless there is no overlap of outcomes, the spinner is not much use for games!
What about the boundary between the segments? Although a magnifying glass may be able to detect which segment the arrow is in when it appears to point to the boundary line between them, it might be more sensible to decide that, if the arrow stops on a boundary line, the colour to the left of that line is taken as the selected colour.
Example C: What colour sweet did you get?
When you give a sweet to your friend by shaking one out of the box onto your friend’s hand, the outcome is the colour of the sweet so there can be only one colour. So if it is red, no other colour is possible. Note that if two sweets come out of the box, it is a different situation; we are considering only the situation of a single sweet coming out of the box.
Example D: Which type of muffin is first to be finished?
With many students choosing muffins at once, it might appear that a tie could happen and two types of muffins could be finished first. Genuine ties almost never happen as mostly “ties” are due to limitations of timing instruments. However this shows that this situation might need more careful description. For example, are the students coming one by one to choose their muffin? Or are we going to say which type is finished first within the space of 1 second of each other?
Notice that these types of situations in which observation depends on the definition of exactly when the event is considered to happen (such as choosing a muffin) and on the accuracy of timing devices, occur in collecting data from queueing situations.
Example E: Where does your newspaper land?
If we describe the possible landing places as the footpath, road, driveway, lawn, garden, then the paper could be on the part of the driveway that is on the footpath. It could be on the part of the grass (lawn) that is on the footpath. There could even be garden on the footpath! Does this mean we should describe the possible landing places so that they do not overlap? Not necessarily - it’s OK to describe the possible events without insisting there is no overlap.
Example F: How many children in a family?
The possible numbers of children in a family are 0, 1, 2, 3, ……. So it is not possible to have exactly 2 children and exactly 3 children. But it is worth looking at this situation again. What might be the most useful way of describing numbers of children in a family? From a planning viewpoint, it might be more useful to describe the possibilities as “at least ….. children in a family”. This also removes the awkwardness of deciding where to stop with the numbers. Often in everyday speech it is sometimes unclear whether people mean exactly or at least; for example, “there are 3 houses with dogs in that street” could mean “exactly 3 houses” or “at least 3 houses” or “to the best of my knowledge at least 3 houses”.
So if it is decided to describe the possible numbers of children in a family by “at least …”, then the possible events are at least 1, 2, 3, …. Notice that at least 0 is everything! In this case all the events have overlap with each other.
Example G: How late is my bus?
If the possible events for the arrival of a bus are described as more than 5 minutes early, up to 5 minutes early, on time, up to 5 minutes late, and more than 5 minutes late, then these events have no overlap provided the cut-off times are identified. For example, what is meant by on time? These events are meant to take the time of arrival of the bus and divide it into non-overlapping intervals. So this situation is like the spinner, where the area of the circle is divided into non-overlapping segments. Like the spinner, just the accuracy or allocation of the measurement on the boundaries between the segments needs to be identified.
Is the chance of an event happening affected or not
affected by the occurrence of another?
Assuming that the chance of an event happening is not affected by the occurrence of another is one of the BIG assumptions across all of statistical modelling and analysis of data. Investigating this assumption is also one of the big challenges of data analysis. We almost always have to make the assumption based on considering what is reasonable in the situation we are considering − which is yet another reason why we need to carefully and clearly describe any situation that involves any kind of random variation.
Here we will make a small start on considering this concept by considering the above simple scenarios involved in games or everyday situations, and some simple extensions of them.
Firstly, notice in all the above examples in which if one event happens then the others cannot, that the chance of an event happening is most definitely affected by the occurrence of another, because it can’t happen! So if we get a 4 on a die, we can’t get anything else. If the spinner lands on red, we can’t get another colour. If there are exactly 2 children in a family, then there are not 3 children in that family. If the bus is early then it’s not late. If a sweet is red, then it’s not any other colour.
That is, in Examples A, B, C, F, and G above, the chance of ANY of the events happening if another occurs is ZERO because none of the others can happen. And for Examples D and E, this will also be the case if we do not allow ties in Example D, and if we distinguish in Example E between driveway (or grass) on the footpath and driveway (or grass) not on the footpath.
So in Example D, if we allow ties − that is, more than one type of muffin could be finished first − do we have a situation where the occurrence of one event is not affected by the occurrence of another? If the white chocolate muffins are finished first, does this affect the chance that the butterscotch muffins are also finished at the same time as the white chocolate ones? We can only assume that it does or does not − we do not know. Do you think it will?
In Example E, if the event landing on the driveway includes the part of the driveway that crosses the footpath, do you think that if the newspaper lands on the driveway, then this affects the chance that it lands on the footpath? That is, if the newspaper lands on the driveway do you think it is more likely to be on the footpath than if it doesn’t land on the driveway? Again, we don’t know; all we can do is say what we think, and say what we assume.
What about the variation of Example F, in which we consider the possible events of a family having at least different numbers of children? Part of this is easier to some extent, because if a family has at least 3 children then they definitely have at least 2. But what about if a family has at least 2 children? Do you think that having at least 2 children affects or doesn’t affect the chance of having at least 3?
So all of the examples above are either completely trivial because if one event happens the others can’t, or all we can do is have interesting discussions about them.
So we will consider a couple of examples based on the above ones, in which it is possible to have two events both happen but slightly easier to consider if the chance of one happening is affected or not by the other happening.
Events used for some games of chance
Example A: Throwing dice
In some games of chance, moves are determined by tossing two dice. So let’s do this by tossing a die twice. Do you think that the chance of a six on the second toss is affected by what we get on the first toss? Not if we toss randomly. So here we can say that, provided we are tossing a die randomly, we can assume that the chance of getting various numbers on the second toss is not affected by what happens on the first toss.
Example B: Spinners
Let’s consider doing two spins − one after the other. Do you think the chance of red on the second spin is affected by the result of the first spin? How do you think the spinning should be done so that we can assume that what happens on the first spin does not affect what happens on the second spin? We would want the spinner to operate in a smooth way, and we would want each spin to be a good spin- that is, not a half-hearted spin. If this is the case, we would be inclined to be comfortable with assuming that the first spin outcome does not affect the second spin out come. For example, the chance of getting red on the second spin is not affected by getting red on the first spin. If you are not completely happy with this assumption, you need to think why you are not. It is not because red is the dominant colour and hence the most likely colour for the spinner to land on. This just means that on any spin, red is the most likely outcome. What we are considering here is if this (greatest) chance of landing on red is the same on the second spin no matter what we get on the first spin.
Example C: What colour sweet did you get?
You shake out a single sweet from your box for your friend. You then shake out another sweet for yourself. Is the chance of your getting a red sweet affected by the colour of the sweet your friend got? Yes, because that first sweet is no longer in the box so there is one less sweet of that colour. What about if you put the first sweet back in the box before you shake out another sweet? (This is not something you would do but it’s just for comparison). Provided you give the box a good shake in between, the colour of the first sweet you got (& then put back) would not affect the colour of the second sweet you get because the situation is exactly the same. But only if you give the box a good shake before shaking out the second sweet.
Example E: Where does your newspaper land today & tomorrow?
If your newspaper lands in your garden today, do you think there is the same chance that it will land in your garden tomorrow? This doesn’t just depend on whether the delivery person is aiming for a certain area, but on whether they change what they do tomorrow because it landed in the garden today. So the assumption here that the chance of the paper landing in the garden tomorrow is not affected by where it landed today, is assuming that the delivery person follows the same routine each day and doesn’t let what happens today affect the way they throw it tomorrow.
Example G: How late is my bus?
If your bus is late arriving today, will this change the chance that it is late arriving tomorrow? Notice this has nothing to do with whether your bus tends to arrive late − it’s to do with whether what happens today affects what happens tomorrow. Perhaps if the morning traffic is bad this morning, lots of people might leave earlier tomorrow morning and this would change the situation tomorrow morning. On the other hand, buses using bus lanes and busways might not be affected by motorists’ decisions to leave earlier or not.
some general comments and links
from F-3 and towards year 5
From Years 1-3, students have gradually developed understanding and familiarity with simple and familiar events involving chance, including possible outcomes and whether they are “likely”, “unlikely” with some being “certain” or “impossible”. They have seen variation in results of simple chance experiments. In Year 4, they consider more carefully how to describe possible outcomes of simple situations involving games of chance or familiar everyday outcomes. Without assigning any values for probabilities, they consider how the probabilities of possible outcomes could compare with each other. They also consider simple everyday events that cannot happen together and, in comparison, some that can. If events cannot both happen, then most definitely, if one happens there is no chance the other can. This helps students start to think about simple situations in which it is reasonable to assume that the occurrence of one event does not affect or change the chance of occurrence of another event.
In Year 5, consideration of the possible outcomes of simple situations leads to assigning equal probabilities in some of these, understanding what the values of these probabilities must be and representing these values using fractions.
The Improving Mathematics Education in Schools (TIMES) Project 2009-2011 was funded by the Australian Government Department of Education, Employment and Workplace Relations.
The views expressed here are those of the author and do not necessarily represent the views of the Australian Government Department of Education, Employment and Workplace Relations.
© The University of Melbourne on behalf of the International Centre of Excellence for Education in Mathematics (ICE-EM), the education division of the Australian Mathematical Sciences Institute (AMSI), 2010 (except where otherwise indicated). This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons.org/licenses/by-nc-nd/3.0/
![]()

