Content description

Solve problems involving the surface area and volume of right prisms (ACMMG218)

Calculate the surface area and volume of cylinders and solve related problems (ACMMG217)

Source: Australian Curriculum, Assessment and Reporting Authority (ACARA)

The surface area of a prism is the sum of the areas of its faces.

Surface area of rectangular prisms

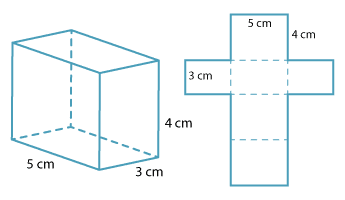
To find the surface area of a rectangular prism or a box, we first flatten it creating the net, and then work out the total surface area by adding the areas of the individual rectangles.

Example 1

Find the surface area of a closed box with base width 3 cm, base length 5 cm and height 4 cm.

Solution

Detailed description

The surface area is then comprised of:

\begin{align}\text{Two rectangular faces with area}\ 3 × 4 &= 12\ \text{cm²}\\ \text{Two rectangular faces with area}\ 3 × 5 &= 15\ \text{cm²}\\ \text{Two rectangular faces with area}\ 4 × 5 &= 20\ \text{cm²}\end{align}

So the surface area is 2 × (12 + 15 + 20) = 94 cm².

In general, if we have a rectangular prism of dimensions \(a × b × c\) then:

The surface area of a rectangular prism = 2(\(ab + ac + bc\)).

Surface area of triangular prisms

A very common example of a triangular prism is the well-known chocolate box.

The base of the triangular prism is a triangle.

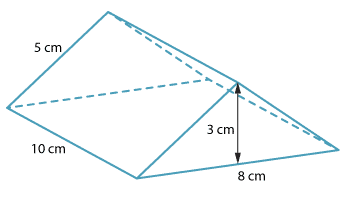
The surface area consists of the area of the two triangles, plus the area of the three rectangles. It can help to draw the shapes separately.

The diagram shows a triangular prism, with isosceles triangles as the ends. All measurements are in centimetres.

Detailed description

The surface area of the prism is calculated as follows:

\begin{align}\text{Two triangular faces with area}\ \dfrac{1}{2}\ × 3 × 8 = 12\ \text{cm²}\\ \text{Two rectangular faces with area}\ 10 × 5 = 50\ \text{cm²}\\ \text{One rectangular face with area}\ 10 × 8 = 80\ \text{cm²}\end{align}

So the surface area is 2(12 + 50) + 80 = 204 cm².