Content description

Graph simple non-linear relations with and without the use of digital technologies and solve simple related equations (ACMNA296)

Source: Australian Curriculum, Assessment and Reporting Authority (ACARA)

Graphs of quadratics

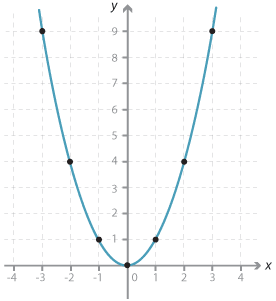
Consider the relationship given by y = x\(^2\). This is not a linear relationship because x is raised to the power 2. First, we complete a table of values.

Table of values

\(x\)	−3	−2	−1	0	1	2	3
\(y = x^2\)	9	4	1	0	1	4	9

We then plot the corresponding points and join them with a smooth curve to obtain the graph below:

Detailed description

This graph is called a parabola. The point (0, 0) is called the vertex or turning point of the parabola. The vertex corresponds to the minimum value of y, since x\(^2\) is positive except when x = 0.

The graph is symmetrical about the y-axis. This line is called the axis of symmetry.

Example 1

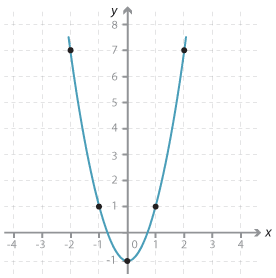
Plot the graph of y = 2 x\(^2\) − 1 for −2 ≤ x ≤ 2. Find the axis of symmetry and the coordinates of the vertex.

Solution

The table of values is shown:

Table of values

\(x\)	–2	–1	0	1	2
\(y = 2 x^2 - 1\)	7	1	–1	1	7

Detailed description

Notice that the y-values are the same for x = −1 and x = 1. The equation of the axis of symmetry is x = 0. When x = 0, y = −1, so the vertex has coordinates (0, −1).

Example 2

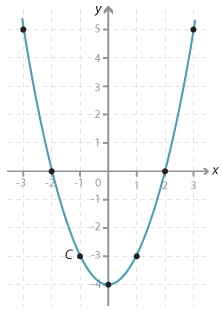
Plot the graph of y = x\(^2\) − 4 for −3 \(\le\) x \(\le\) 3. Give the coordinates of the vertex, the equation of the axis of symmetry and the coordinates of the x-intercepts and the y-intercept.

Solution

The table of values is shown:

Table of values

\(x\)	−3	−2	−1	0	1	2	3
\(y = x^2 - 4\)	5	0	−3	−4	−3	0	5

Detailed description

The vertex has coordinates (0, −4).

The equation of axis of symmetry is x = 0.

The coordinates of the y-intercept are (0, −4).

The coordinates of the x-intercepts are (−2, 0) and (2, 0).