Content description

Develop the formulas for volumes of rectangular and triangular prisms in general. Use formulas to solve problems involving volume (ACMMG198)

Elaboration

• investigating the relationship between volumes of rectangular and triangular prisms

Source: Australian Curriculum, Assessment and Reporting Authority (ACARA)

Volume of triangular prisms

We will generally say 'prism' when we really mean 'right prism'. A prism has uniform cross-section. This means that when you take slices through the solid parallel to the base you get polygons congruent to the base. So the area of each slice is always the same. In a rectangular prism, the cross-section is always a rectangle.

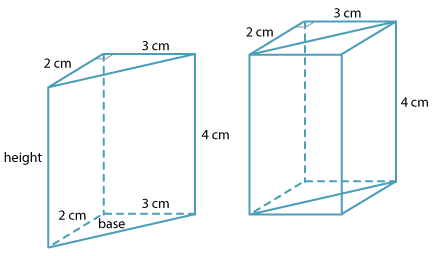
In a triangular prism, each cross-section parallel to the triangular base is a triangle congruent to the base. In the diagram below the triangular prism is not 'standing' on its triangular base.

Suppose we have a triangular prism whose height is 4 cm as shown in the diagram.

Detailed description

This prism can be thought of as the rectangular prism with dimension 2 × 3 × 4 cut in half.
Hence the volume of the triangular prism = \(\dfrac{1}{2}\) × 2 × 3 × 4 cm³
In this case, the base of the prism is a right-angled triangle. The lengths of its shorter sides are 2 cm and 3 cm respectively.
The area of the triangle = \(\dfrac{1}{2}\) × 2 × 3 cm².
The volume of the prism is given by the area of the base of the prism multiplied by the height:

\begin{align}V &= 3 × 4\\\\ &= 12\ \text{cm}^3\end{align}

So the volume of any triangular prism whose base has area A and whose height (or depth) is h is given by: