Teacher resources icon

The interior angles of a quadrilateral have a sum of 360°

This can be demonstrated by tearing off the corners and showing that they fit together to form a revolution, or by drawing quadrilaterals and measuring the angles. But it can be proved.

Theorem

The sum of the interior angles in a quadrilateral is 360°.

Proof

There are two kinds of quadrilaterals, as shown in the diagrams below. When one diagonal is drawn, two triangles are formed. The angle sum of each triangle is 180°. Hence the angle sum of the quadrilateral is 360°.

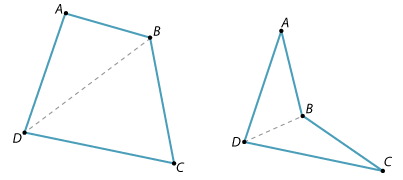
Two diagrams. Convex quadrilateral ABCD with dashed diagonal BD. Non-convex quadrilateral ABCD with dashed diagonal BD.

Example 2

Find the value of θ in the following quadrilateral.

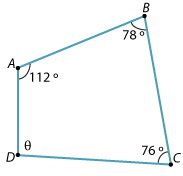
Quadrilateral ABCD. Angle A 112 degrees, angle B 78 degrees, angle C 76 degrees, angle D theta.

Solution

θ + 112° + 78° + 76° = 360°

Hence θ = 94°.