Teacher resources icon

Alternate angles

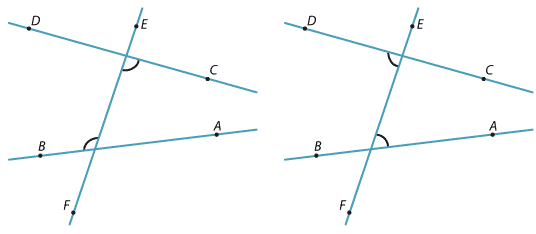
In each diagram below, the two marked angles are called alternate angles because they are on alternate sides of the transversal EF. The two angles must be between the two lines.

Two diagrams. Both have a pair of lines AB and CD cut by a transversal EF.

Alternate angles and parallel lines

When the lines AB and CD are parallel (as in the diagram below), the alternate angles \(\angle\)BHF and \(\angle\)CGE are equal.

This can be proven using the previous result that showed that corresponding angles are equal.

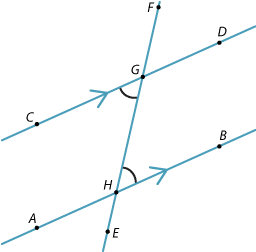
Pair of parallel lines AB and CD cut by a transversal EF at points G and H. Angle CGE equals angle BHF.

\(\angle\)BHF = \(\angle\)DGF (corresponding AB || CD)

\(\angle\)DGF = \(\angle\)CGE (vertically opposite angles at G)

Hence \(\angle\)BHF =\(\angle\)CGE.

Example 2

Find θ in the diagram.

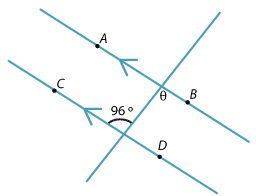
Pair of parallel lines AB and CD cut by a transversal. One angle marked 96 degrees and the alternate angle marked theta.

Solution

θ = 96° (alternate angles AB || CD)