Content description

Given coordinates, plot points on the Cartesian plane, and find coordinates for a given point (ACMNA 178)

Elaboration

• plotting points from a table of integer values and recognising simple patterns, such as points that lie on a straight line

Source: Australian Curriculum, Assessment and Reporting Authority (ACARA)

Tables and plotting points

Two friends play a simple game to improve their multiplication skills. Sally calls out a number and James multiplies it by 2. Sally starts at –2 and calls out to James each integer up to 2. Their results are recorded in a table below.

Sally's number	–2	–1	0	1	2
James's number	–4	–2	0	2	4

We can write the rule as:

James's number = 2 × Sally's number.

If we let x represent Sally's number and y represent James's number then we can write the rule as:

y = 2x

We can also plot the points in the table on the Cartesian plane as shown below.

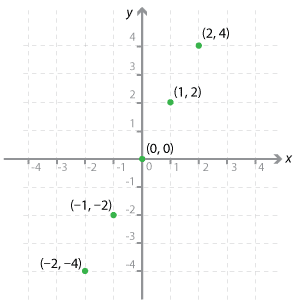
Look carefully at the points and notice that you can take a ruler and draw a straight line through these points.

We can follow this procedure for any similar rule by forming a table and plotting the corresponding points.

Example 1

For each given rule:

1. complete the table
2. list the coordinates of the points
3. plot the points on the Cartesian plane.

1. y = –x
   

   x	–3	–2	–1	0	1	2	3
   y

2. y = x + 1
   

   x	–3	–2	–1	0	1	2	3
   y

Solution

ay = –x

1. x	–3	–2	–1	0	1	2	3
   y	3	2	1	0	–1	–2	–3

2. The points are (–3, 3), (–2, 2), (–1, 1), (0, 0), (1, –1), (2, –2), and (3, –3).
3. 

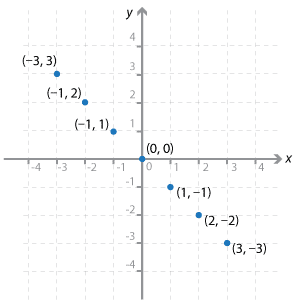
b y = x + 1

1. x	–3	–2	–1	0	1	2	3
   y	–2	–1	0	1	2	3	4

2. The points are (–3, –2), (–2, –1), (–1, 0), (0, 1), (1, 2), (2, 3) and (3, 4).
3. 

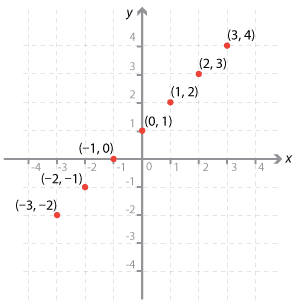
Notice that in both these examples, the points can be joined to form a straight line.