Teacher resources icon

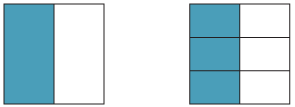
Using squares

We can use squares to see that the area representing \(\dfrac{1}{2}\) equals the area representing \(\dfrac{3}{6}\).

Two squares, left square half shaded, right square 3/6 shaded


Equivalent improper fractions

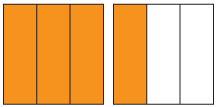
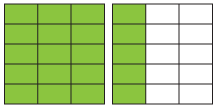
We can use squares to show that \(\dfrac{4}{3}\) is equivalent to \(\dfrac{20}{15}\). The area of each large square is 1.

  1. Two squares both divided into thirds. Left square shaded and right square with 1/3rd shaded.
  2. Two squares both divided into 1/15ths. Left square shaded and right square with 1/3rd shaded.

Shaded area A represents the fraction \(\dfrac{4}{3}\) and shaded area B represents the fraction \(\dfrac{20}{15}\). The two areas are the same, so \(\dfrac{4}{3}\) is equivalent to \(\dfrac{20}{15}\).