Example

Both Sydney (Australia) and Cape Town (South Africa) are on the ${33.5^{\circ}}$ S parallel of latitude, but Sydney is at ${151.13^{\circ}}$ E whereas Cape Town is at ${18.22^{\circ}}$ E. How far is it from Sydney to Cape Town travelling the great circle route, correct to the nearest km?

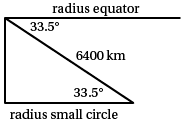
Solution

For the small circle,

$\begin{aligned}[t] &r =6400\times \cos 33.5^{\circ}\\ &=5336.869\ldots \\ &\approx 5337\text{ km} \end{aligned}$

Longitude angle difference for Sydney and Cape Town is ${151.13^{\circ}} - {18.22^{\circ}} = {132.91^{\circ}}$.

Straight line distance from Sydney to Capetown

$\begin{aligned} d& = \sqrt{5337^2 + 5337^2 - 2 \times 5337 \times 5337 \times \text{ cos} 132.91^{\circ}}\\ & = 9785 \text{ km} \end{aligned}$

Angle between earth radii

$\begin{aligned} \theta& = \cos^{-1} \left(\frac{6400^2 + 6400^2 - 9785^2}{2 \times 6400 \times 6400}\right)\\ & = 99.72^{\circ} \end{aligned}$

From Sydney to Cape Town via great circle route

$\begin{aligned} &=\frac{r\pi}{180^{\circ}}\times\theta\\ & =\frac{6400\pi}{180^{\circ}}\times 99.72^{\circ}\\ & =11138.831\ldots \approx 11139\text{ km} \end{aligned}$

We can see that, compared to the distance around the ${33.5^{\circ}}$ parallel of latitude which was 12380 km, the great circle route at 11139 km is some 1241 km shorter.

Example

Both Launceston (Tasmania, Australia) and Puerto Monti (Chile, South America) are on the ${41.3^{\circ}}$ S parallel of latitude, but Launceston is at ${147.08^{\circ}}$ E whereas Puerto Monti is at ${72.57^{\circ}}$ W. How far is it from Launceston to Puerto Monti travelling the great circle route, correct to the nearest km?

Solution

For the small circle,

$\begin{aligned}[t] r & =6400\times \cos {41.3^{\circ}}\\ & =4808.090\ldots \\ &\approx 4808\text{ km} \end{aligned}$

The angle between the longitude of Launceston and that of Puerto Monti is ${147.08^{\circ}} + {72.57^{\circ}} = {219.65^{\circ}}$. We find the sum since these places are on different sides of the Prime Meridian, but this is the major arc, and the minor arc will be ${360^{\circ}} - {219.65^{\circ}} = {140.35^{\circ}}$.

Straight line distance from Launceston to Puerto Monti

$\begin{aligned}[t] d& = \sqrt{4808^2 + 4808^2 - 2 \times 4808 \times 4808 \times \text{ cos} 140.35^{\circ}} \\ & = 9046 \text{ km} \end{aligned}$

Angle between earth radii

$$ \theta = \cos^{-1} \left(\frac{6400^2 + 6400^2 - 9046^2}{2 \times 6400 \times 6400}\right) = 89.94^{\circ}$$

From Launceston to Puerto Monti via great circle route

$\begin{aligned}[t] &=\frac{r\pi}{180^{\circ}}\times\theta\\ & =\frac{6400\pi}{180^{\circ}}\times 89.94^{\circ} \\ &=10046.394\ldots &\approx 10046\text{ km} \end{aligned}$