Example

Both Sydney (New South Wales) and Margaret River (Western Australia) are on the ${33.5^{\circ}}$ S parallel of latitude, but Sydney is at ${151.13^{\circ}}$ E whereas Margaret River is at ${115.04^{\circ}}$ E.

How far is it from Sydney to Margaret River travelling along the ${33.5^{\circ}}$ S parallel, correct to the nearest km?

Solution

First we need to calculate the radius of the small circle that forms the ${33.5^{\circ}}$ S parallel of latitude.

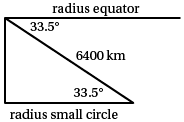
In the right-angle triangle shown right, the hypotenuse is the radius of the Earth (6400 km), the angle is ${33.5^{\circ}}$ and the radius of the small circle is the side adjacent to the angle.

We can use cosine relationship in standard trigonometry to find the required value.

For the small circle,

$\begin{aligned}[t] r&={6400} \times \cos {33.5^{\circ}}\\ & ={5336.869} \ldots \\ &\approx {5337}\text{ km} \end{aligned}$

Longitude angle difference for Sydney and Margaret River is ${151.13^{\circ}} - {115.04^{\circ}} = {36.09^{\circ}}$.

(We find the difference since BOTH places are on the SAME side of the Prime Meridian)

From Sydney to Margaret River

$$l=\frac{r\pi}{180^{\circ}}\times\theta=\frac{5337\pi}{180^{\circ}}\times 36.09^{\circ}=3361.719\ldots\approx 3362\text{ km}$$

Example

Both Hamilton (Western Victoria) and Orbost (Gippsland) are on the ${37.4^{\circ}}$ S parallel of latitude, but Hamilton is at ${142.02^{\circ}}$ E whereas Orbost is at ${148.27^{\circ}}$ E. How far is it from Hamilton to Orbost travelling along the ${37.4^{\circ}}$ S parallel, correct to the nearest km?

Solution

For the small circle, $r =6400\times \cos 37.4^{\circ} =5084.253\ldots \approx 5084\text{ km}$

Longitude angle difference for Hamilton and Orbost is ${148.27^{\circ}} - {142.02^{\circ}} = {6.25^{\circ}}$.

From Hamilton to Orbost

$${l}=\frac{r\pi}{180^{\circ}}\times\theta =\frac{5084\pi}{180^{\circ}}\times 6.25^{\circ} =554.578\ldots \approx 555\text{ km}$$

Example

Both Sydney (Australia) and Cape Town (South Africa) are on the ${33.5^{\circ}}$ S parallel of latitude, but Sydney is at ${151.13^{\circ}}$ E whereas Cape Town is at ${18.22^{\circ}}$ E. How far is it from Sydney to Cape Town travelling along the ${33.5^{\circ}}$ S parallel, correct to the nearest km ?

Solution

For the small circle, $r =6400\times \cos 33.5^{\circ} =5336.869\ldots \approx 5337\text{ km}$

Longitude angle difference for Sydney and Cape Town is ${151.13^{\circ}} - {18.22^{\circ}} = {132.91^{\circ}}$.

From Sydney to Cape Town

$${l}=\frac{r\pi}{180^{\circ}}\times\theta =\frac{5337\pi}{180^{\circ}}\times 132.91^{\circ} =12380.330\ldots \approx 12380\text{ km}$$

Example

Both Launceston (Tasmania, Australia) and Puerto Monti (Chile, South America) are on the ${41.3^{\circ}}$ S parallel of latitude, but Launceston is at ${147.08^{\circ}}$ E whereas Puerto Monti is at ${72.57^{\circ}}$ W. How far is it from Launceston to Puerto Monti travelling over the southern Pacific ocean along the ${41.3^{\circ}}$ S parallel, correct to the nearest km?

Solution

For the small circle, $r =6400\times \cos {41.3^{\circ}} =4808.090\ldots \approx 4808\text{ km}$

The angle between the longitude of Launceston and that of Puerto Monti is ${147.08^{\circ}} + {72.57^{\circ}} = {219.65^{\circ}}$. We find the sum since these places are on different sides of the Prime Meridian, but this is the major arc, and the minor arc will be ${360^{\circ}} - {219.65^{\circ}} = {140.35^{\circ}}$.

From Launceston to Puerto Monti

$${l}=\frac{r\pi}{180^{\circ}}\times\theta =\frac{4808\pi}{180^{\circ}}\times 140.35^{\circ} =11777.530\ldots \approx 11778\text{ km}$$