Content
Distance between places on the Equator
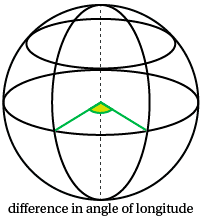
The Equator is a great circle, and hence finding the distance between two points on the Equator uses the same calculation process as for finding the distance between two points on the same meridian of longitude.
Example
Both Libreville (Gabon) and Kismanyo (Somalia) are on the Equator on opposite sides of the African continent. Libreville is at ${9.27^{\circ}}$ E and Kismanyo is at ${42.32^{\circ}}$ E.
How far is it from Libreville to Kismanyo travelling along the Equator, correct to the nearest km?
Solution
The Equator is a great circle, with a radius of 6400 km.
The angle between the longitude of Libreville and that of Kismanyo is ${42.32^{\circ}}$ ? ${9.27^{\circ}}$ = ${33.05^{\circ}}$.
(We find the difference since both places have the same longitude direction (E))
From Libreville to Kismanyo
\begin{align*} l &=\frac{r\pi}{180^{\circ}}\times\theta \\ &=\frac{6400\pi}{180^{\circ}}\times 33.05^{\circ}\\ &=3691.720\ldots \\ &\approx 3692\text{ km} \end{align*}Example
Both the Galapagos Islands and the island of Naura are on the Equator, but the Galapagos Islands are at ${90.30^{\circ}}$ W whereas the island of Nauru is at ${166.56^{\circ}}$ E.
How far is it from the Galapagos Islands to Nauru travelling over the Pacific ocean along the Equator, correct to the nearest km ?
Solution
The angle between the longitude of the Galapagos Islands and that of Nauru is ${90.30^{\circ}} + {166.56^{\circ}} = {256.86^{\circ}}$. We find the sum since these places have different longitude directions, but this is the major arc, and the minor arc will be ${360^{\circ}} - {256.86^{\circ}} = {103.14^{\circ}}$.
We could also find the angle between these two places by recognising that both are close to ${180^{\circ}}$E/W. We could find the angle between the Galapagos Islands and ${180^{\circ}}$E/W, the island of Nauru and ${180^{\circ}}$E/W, and then add these two angles together.
Angle between Galapagos Islands and ${180^{\circ}}$E/W = ${180^{\circ}}$ - ${90.30^{\circ}}$ = ${89.70^{\circ}}$.
Angel between Nauru island and ${180^{\circ}}$E/W = ${180^{\circ}}$ - ${166.56^{\circ}}$ = ${13.44^{\circ}}$
Total angle between Galapagos Islands and Nauru = ${89.70^{\circ}}$ + ${13.44^{\circ}}$ = ${103.14^{\circ}}$
From the Galapagos Islands to Nauru
\begin{align*} l &=\frac{r\pi}{180^{\circ}}\times\theta \\ &=\frac{6400\pi}{180^{\circ}}\times 103.14^{\circ} \\ &=11520.848\ldots \\ &\approx 11521\text{ km} \end{align*}Next page - Content - Distances between places with the same latitude
