Content
Latitude and Longitude
Latitude
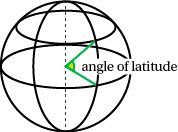
Latitude is a measure of the position of a point on the earth's surface in terms of degrees north or south of a baseline - the equator. These values vary from ${90^{\circ}}$S to ${90^{\circ}}$N. The latitude of the Equator is ${0^{\circ}}$.Every plane perpendicular (at right angles) to the earth's axis cuts the surface of the earth in a circle called a parallel of latitude.
The parallel of latitude formed by a plane passing through the centre of the earth and equidistant from both the North and South Poles is called the equator. All other parallels of latitude are small circles, each having a radius smaller than that of the earth, i.e. less than 6400 km. As the parallels run east and west, places having the same latitude will be due east or due west of each other.
Distance north or south of the equator is calculated from the arc length using the angle between two radii - one going to the equator and the other going to the point whose latitude is required.
Latitude is determined by measuring the angle of elevation of the sun at noon, and adding or subtracting an allowance for the time of year. Using the angle only is correct for just two days of the year - the spring and autumnal equinoxes. In midwinter we need to subtract ${23.45^{\circ}}$ and at midsummer we need to add ${23.45^{\circ}}$. These allowances are due to the fact that the earth is tilted at this angle as it orbits the sun. Books of correction factors for every day of the year (almanacs) were used for many years until global positioning satellites were used.
Longitude
In the same way that latitude fixes a place north or south of the equator, longitude fixes a place east or west of the prime meridian - also known as the Greenwich meridian which passes through Greenwich near London, UK.
Each great circle passing through the north and south poles has the earth's axis as its diameter. Each great circle is divided by the poles into two semi-circles called meridians of longitude. As the meridians run north and south, places having the same longitude will be due or due south of each other.

Distance east or west of Greenwich is measured as an angle between the plane containing the Greenwich meridian and the plane containing the meridian passing through the point whose longitude is required.
Longitude varies from ${180^{\circ}}$ W of Greenwich to ${180^{\circ}}$ E of Greenwich.
The two meridians on a particular great circle will have values which sum to ${180^{\circ}}$, but one will have a designation W and the other a designation E. For example, ${60^{\circ}}$W is on the same great circle as ${120^{\circ}}$E.
The accurate determination of longitude was one of the great technological challenges of the eighteenth century, since a number of shipping disasters had shown up the inadequacies of the methods being used at the time. A number of European nations offered financial prizes for the development of a reliable and accurate method for determining longitude.
The Earth rotates at a rate of ${360^{\circ}}$ per day, or ${15^{\circ}}$ per hour, so there is a direct relationship between time and longitude. If a navigator knew the time at a particular fixed reference point when the local time could be determined at the ship's location, the difference between the reference time and the apparent local time would give the ship's position relative to the fixed location.
Two methods were in common use.
One involved measuring the lunar distance - the angle between the Moon and another celestial object (a star or the sun) - which would lead to determination of the position of the measurer through calculation based on reference values. This method required the compilation of tables of reference values (an almanac) for every day of every year well in advance of their required use - a task which required a lot of human calculating time in a pre-electronic computer era.
The second, and simpler, method involved taking a chronometer, which could keep very accurate time at sea, and calculate position almost immediately by comparing the chronometer time for the fixed reference point with local time. It took until the 1850's to build accurate chronometers cheap enough for their widespread use.
The advent of radio in the early twentieth century enabled navigators to verify the accuracy of their chronometers with time signals broadcast from known locations. Global positioning satellite systems and radar have added to the tools available to the modern navigator.
Locating positions on Earth
The position of any point on the earth's surface is given uniquely by the intersection of the circles of latitude and longitude.
By convention, the latitude is given first when giving the position of any point.
Example
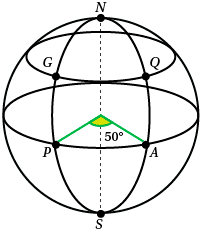
In the diagram , the meridian through $NGPS$ is the Greenwich meridian. Points $G$ and $Q$ are on the ${40^{\circ}}$ N parallel of latitude. Points $P$ and $A$ are on the equator. Write down the positions of points $G$, $Q$, $A$ and $P$
Solution
$$G ({40^{\circ}} N, {0^{\circ}} E (or W))$$ $$Q ({40^{\circ}} N, {50^{\circ}} E)$$ $$A ({0^{\circ}} N (or S), {50^{\circ}} E)$$ $$P ({0^{\circ}} (N or S), {0^{\circ}} E)$$