Content
Calculation Notes
Unless it is specifically requested, the $\pi$ value obtained by accessing the appropriate function in a scientific or graphic calculator should be used in any calculation involving ${\pi}$.
ALL angles in this unit will be specified in degrees.
Measuring arc length
In any circle, the length of an arc ($l$) is proportional to the angle ($\theta$) it creates (subtends) at the centre.
For a circle of radius $r$, the circumference will be $2\pi$ units.
Thus,
$$\frac{\text{the length of the arc}}{\text{circumference}}=\frac{\theta}{360^{\circ}},$$so $\begin{aligned}[t] &\frac{l}{2\pi r } = \frac{\theta}{360^{\circ}}.\\ \therefore l &= \frac{\theta}{360^{\circ}} \times {2\pi r}\\ &= \frac{\theta}{180^{\circ}} \times {\pi r}\\ &= {r} \times \frac{\pi}{180^{\circ}} \times {\theta} \text{ (Alternate formulations)} \end{aligned}$
Example
A circle has a radius of 30 cm. Find the length of an arc subtending an angle of ${75^{\circ}}$ at the centre, correct to one decimal place.
Solution
$\begin{aligned}[t] \mbox{Length of arc}&=\frac{r\pi}{180^{\circ}}\times\theta\\ &=\frac{30\pi}{180^{\circ}}\times 75^{\circ}\\ &=39.2699\ldots\\ &\approx 39.3\text{ cm} \end{aligned}$Example
An arc of a circle has a length of 30 cm. If the radius of the circle is 25 cm, what angle, correct to the nearest whole degree, does the arc subtend at the centre?
Solution
$\begin{aligned}[t] 30&=\frac{r\pi}{180^{\circ}}\times {\theta}\\ &=\frac{25\pi}{180^{\circ}}\times {\theta}\\ \theta &=\frac{30 \times 180^{\circ}}{25 \times \pi}\\ &=68.754\ldots\approx {69^{\circ}} \end{aligned}$Sector
The area of a sector depends not only on the radius of the circle involved, but also the angle between the two straight edges.
We can see this in the following table :
| Angle | Fraction of circle area | Area rule |
| \(180^{\circ}\) | $\dfrac{180^{\circ}}{360^{\circ}}=\dfrac{1}{2}$ | ${A}=\dfrac{1}{2}\times {\pi r^2}$ |
| $90^{\circ}$ | $\dfrac{90^{\circ}}{360^{\circ}}=\dfrac{1}{4}$ | ${A}=\dfrac{1}{4}\times {\pi r^2}$ |
| $45^{\circ}$ | $\dfrac{45^{\circ}}{360^{\circ}}=\dfrac{1}{8}$ | ${A}=\dfrac{1}{8}\times {\pi r^2}$ |
| $30^{\circ}$ | $\dfrac{30^{\circ}}{360^{\circ}}=\dfrac{1}{12}$ | ${A}=\dfrac{1}{12}\times {\pi r^2}$ |
| ${\theta}$ | $\dfrac{\theta}{360^{\circ}}$ | ${A}=\dfrac{\theta}{360}\times {\pi r^2}$ |
Example
Find the area of a sector with a radius of 40 mm, that contains an angle of ${60^{\circ}}$, correct to the nearest square millimetre.
Solution
$$A=\frac{\theta}{360^{\circ}}\times {\pi r^2}=\frac{60^{\circ}}{360^{\circ}}\times {\pi 40^2}=923.628\ldots \approx 924\text{ mm}^2$$Areas of segments
Where a chord subtends an angle ${\theta}$ at the centre of a circle of radius $r$, the area of the minor segment is given by:
\[\text{ Area} = \frac{1}{2} \times {r^2} \left(\frac{2 \pi \theta}{360^{\circ}} - {\sin \theta}\right)\]The area of the sector that includes the segment is given by $A=\dfrac{\theta}{360^{\circ}}\times {\pi r^2}$
or rewritten as
\[A = \dfrac{1}{2}\times {r^2} \times \dfrac{2 \pi \theta}{360^{\circ}}.\]The area of the triangle whose boundaries are the two radii and the chord is given by
$\dfrac{1}{2}\times {r^2} \times {\sin \theta} \qquad \left(\text{from the Sine Area Rule} \quad \dfrac{1}{2}\times {ab} \sin {C}\right).$Hence the area of the segment (minor) can be calculated by subtracting the area of the triangle from the area of the sector.
The area of the major segment can be calculated by taking the area of the minor segment from the total area of the circle.
Example
Find the area, correct to two decimal places, of the minor segment in a circle of radius 10 cm where the angle subtended at the centre of the circle by the chord is ${85^{\circ}}$.
Solution
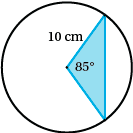$\begin{aligned}[t]
&\mbox{ Area}\\
&= \frac{1}{2} \times {r^2} \left(\frac{2 \pi \theta}{360^{\circ}} - {\sin \theta}\right)\\
& = \frac{1}{2} \times {10^2} \left(\frac{2 \times \pi \times 85^{\circ}}{360^{\circ}} - {\sin {85}^{\circ}}\right) \\
&= 24.366\ldots \\
&\approx 24.37\text{cm}^2
\end{aligned}$
Example
Find the area, correct to one decimal place, of the minor segment in a circle, of radius 15 cm where the chord length is also 15 cm.
Solution
If the chord length is the same as the radius of the circle, then the triangle that is formed will be equilateral (all three sides are 15 cm!), and the angle subtended at the centre by the chord will be ${60^{\circ}}$ (the angle inside an equilateral triangle).
$$ \text{Area} = \frac{1}{2} \times {r^2} \left(\frac{2 \pi \theta}{360^{\circ}} - {\sin \theta}\right) = \frac{1}{2} \times {15^2} \left(\frac{2 \times \pi \times 60^{\circ}}{360^{\circ}} - {\sin 60^{\circ}}\right)= 20.381\ldots \approx 20.4\text{ cm}^2$$Example
Find the area, correct to two decimal places, of the minor segment in a circle, of radius 13 cm where the chord length is 21 cm.
Solution
To find the angle subtended at the centre by the chord, we will have to use the Cosine Rule
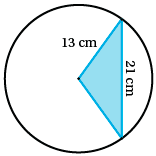\begin{align*}
A& = \cos^{-1} \left(\frac{b^2 + c^2 - a^2}{2bc}\right)\\
\mbox{ where} b& = c = \mbox{radius}\\
a& = \mbox{chord length}, \\
A&= \mbox{angle subtended at centre of circle}.\\
\text{So A}& = \cos^{-1} \left(\frac{13^2 + 13^2 - 21^2}{2 \times 13 \times 13}\right)\\
& = 107.74^{\circ}
\end{align*}
\begin{align*}
\text{ Area}&= \frac{1}{2} \times {r^2} \left(\frac{2 \pi \theta}{360^{\circ}} - {\sin \theta}\right)\\
&= \frac{1}{2} \times {13^2} \left(\frac{2 \times \pi \times 107.74^{\circ}}{360^{\circ}} - {\sin 107.74^{\circ}}\right)\\
&= 78.409\ldots\\
&\approx 78.41\text{ cm}^2
\end{align*}
Next page - Content - The Earth as a sphere
 |
These materials have been developed in collaboration with the Victorian Curriculum and Assessment Authority. © VCAA and The University of Melbourne on behalf of AMSI 2015 |
Contributors Term of use |