Content

A circle is formed by a point moving around a fixed point (the centre) at a constant distance.

A sphere is a three-dimensional form of a circle, where all points on the surface of the sphere are at a constant distance from the centre of the sphere.

The Earth is not exactly a sphere. A grapefruit is a better analogy, as it is flatter at the top and bottom (an oblate sphere). The diameter as measured through the North and South Poles is about 40 km less than the diameter using two points on the Equator. The radius of the Earth is usually given as 6 370 kilometres.

For the purposes of modelling key aspects of travel and time on the Earth, for a course such as Further Mathematics in the Victorian Certificate of Education, treating the Earth as a true sphere with a radius of 6 400 kilometres will provide reasonable answers from a conceptually simple framework.

Circular Geometry

Radii and chords

We begin by revisiting the definition of a circle and some of the language used for describing the geometry of circles.

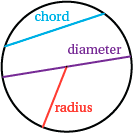
• A circle is the set of all points in the plane that are a fixed distance (the radius) from a fixed point (the centre).
• Any interval joining a point on the circle to the centre is called a radius. By the definition of a circle, any two radii have the same length.
• An interval joining two points on the circle is called a chord.
• A chord that passes through the centre is called a diameter. Since a diameter consists of two radii joined at their endpoints, every diameter has length equal to twice the radius.

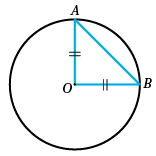
Let $AB$ be a chord of a circle not passing through its centre $O$. The chord and the two equal radii $OA$ and

$BO$ form an isosceles triangle whose base is the chord. The $\angle AOB$ is called the angle at the centre

subtended by the chord.

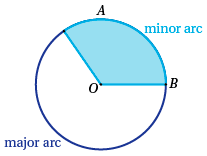
Let $A$ and $B$ be two different points on a circle with centre $O$. These two points divide the circle into two opposite arcs. If the chord $AB$ is a diameter, then the two arcs are called semicircles. Otherwise, one arc is longer than the other. The longer arc is called the major arc $AB$ and the shorter arc is called the minor arc $AB$.

Now join the radii $OA$ and $OB$. The reflex angle $AOB$ is called the angle subtended by the major arc $AB$. The non-reflex angle $AOB$ is called the angle subtended by the minor arc $AB$, and is also the angle subtended by the chord $AB$.

The two radii divide the circle into two sectors, called correspondingly the major sector $OAB$ and the minor sector $OAB$.

Segments

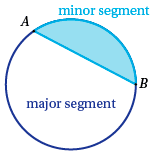
A chord $AB$ of a circle divides the circle into two segments. The two segments are called a major segment (the larger one) and a minor segment (the smaller one).

Subtend

The word 'subtend' literally means 'holds under', and is often used in geometry to describe an angle. The phrase 'opposite to' could also be used, since, in the case above, the angle subtended by an arc is located opposite to that arc in the diagram.

Next page - Content - Calculations Notes