Content

Transformations of graphs

A common type of problem asks you to transform a graph $y = f(x)$, and find the equation of the transformed graph. We illustrate with an example.

Example

Consider the graph $y = x^2$. Suppose the graph is dilated from the $x$-axis by a factor of $2$, and then translated $3$ units to the right. What is the equation of the resulting graph?

Solution

The transformation given is $\text{Trans}_{(3,0)} \circ \text{Dil}_{\text{$x$-axis},2}$. Denote by $(x',y')$ the image of a point $(x,y)$ under this transformation. A point $(x,y)$ is sent to $(x,2y)$ by the dilation, and then to $(x+3,2y)$ by the translation, so $(x',y') = (x+3,2y)$.

The original graph consists of points $(x,y)$ such that $y=x^2$. Then it is transformed so that $(x,y) \mapsto (x',y') = (x+3,2y)$. We must find what equation is satisfied by $x'$ and $y'$.

Since $x' = x+3$ and $y' = 2y$, we have $x = x' - 3$ and $y = y' / 2$. Thus $y = x^2$ implies

\[ \frac{y'}{2} = (x' - 3)^2 \quad \text{or equivalently} \quad y' = 2 (x' - 3)^2. \]

Thus, after the transformation, the graph consists of points $(x,y)$ satisfying $y = 2(x-3)^2$. This is the equation of the transformed graph.

Exercise 33

In the above example, suppose the translation was applied first, then the dilation. Would the answer have been different?

The method in this example can be used generally to find an equation for a graph subject to a transformation $F: \mathbb{R}^2 \rightarrow \mathbb{R}^2$.

Write $(x', y' ) = F(x,y)$, and invert this equation to write $x$ and $y$ as expressions in terms of $x'$ and $y'$.
Substitute these expressions for $x$ and $y$ into the equation of the graph to obtain an equation in $x'$ and $y'$.
The transformed graph then consists of points $(x',y')$ satisfying this equation in $x'$ and $y'$. Dropping the primes, we have an equation in $x$ and $y$ for the transformed graph.

Example

Consider the graph $y = e^x$. Suppose the graph is dilated from the $y$-axis by a factor of $3$, reflected in the $x$-axis, and then translated $1$ unit to the left and $2$ units down. What is the equation of the resulting graph?

Solution

A point $(x,y)$ maps to $(3x,y)$ under the dilation, then to $(3x,-y)$ under the reflection, then to $(3x-1,-y-2)$ under the translation. So $(x',y') = (3x-1,-y-2)$. Inverting, we obtain $x = \frac{x'+1}{3}$ and $y = -y'-2$. Substituting these expressions into $y = e^x$ gives $-y'- 2 = e^{\frac{x'+1}{3}}$. So the equation of the transformed graph is

\[ y = -2 - e^{\frac{1}{3}(x+1)}. \]

Exercise 34

Suppose that in the above example the transformations were applied in the reverse order: translations, then reflection, then dilation. Is the answer any different?

Commonly, a graph $y = f(x)$ is transformed by a combination of dilations from the axes, and a translation. The following theorem gives a formula for the resulting graph.

Theorem

Suppose the graph of $y = f(x)$ is transformed by a dilation of factor $k$ from the $x$-axis, factor $h \neq 0$ from the $y$-axis, and then translated by the vector $(c,d)$ (i.e. $c$ units to the right and $d$ units up). The resulting graph has equation

\[ y = k f \left( \frac{1}{h} (x-c) \right) + d. \]

Note that if there is a reflection in the $x$-axis, then we can take $k$ to be negative; and if there is a reflection in the $y$-axis, we can take $h$ to be negative.

Proof

The point $(x,y)$ is mapped to $(hx,ky)$ under the dilations, then to $(hx+c,ky+d)$ under translation, so $x' = hx+c$ and $y' = ky+d$. Inverting these equations (assuming $h,k \neq 0$) gives

\[ x = \frac{1}{h} \left( x' - c \right) \quad \text{and} \quad y = \frac{1}{k} \left( y' - d \right). \]

The graph with equation $y = f(x)$ is thus taken under the transformation to points $(x',y')$ such that

\[ \frac{1}{k} \left( y' - d \right) = f \left( \frac{1}{h} \left( x' - c\right) \right), \quad \text{which simplifies to} \quad y' = k f \left( \frac{1}{h} \left( x' - c \right) \right) + d. \]

We may now drop the primes and we obtain the desired equation.

There is also the possibility $k=0$. In this case dilation projects the graph to $y=0$, then translation takes it to $y=d$, agreeing with the formula.

$\Box$

While questions involving translations and dilations in the axes are most common, the same method applies to general transformations.

Example

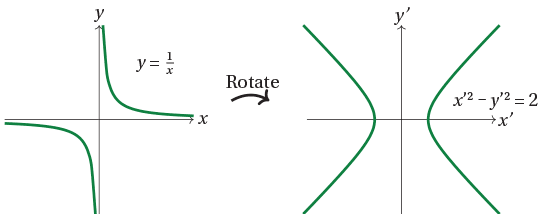
The hyperbola given by $y = 1/x$ is rotated by $45^\circ$ clockwise about the origin. What is the equation of the resulting curve?

Solution

The point $(x',y')$ is obtained by rotating $(x,y)$ by $- \frac{\pi}{4}$, and $(x,y)$ is obtained by rotating $(x',y')$ by $\frac{\pi}{4}$ about the origin. Thus

\[ \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} \cos \frac{\pi}{4} & - \sin \frac{\pi}{4} \\ \sin \frac{\pi}{4} & \cos \frac{\pi}{4} \end{bmatrix} \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \frac{1}{\sqrt{2}} & \frac{-1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{bmatrix} \begin{bmatrix} x' \\ y' \end{bmatrix} = \frac{1}{\sqrt{2}} \begin{bmatrix} x' - y' \\ x' + y' \end{bmatrix}. \]

Hence the curve $y=1/x$, or $xy = 1$, is mapped to points $(x',y')$ such that

\[ \frac{1}{2} (x' - y')(x' + y') = 1, \quad \text{that is,} \quad x'^2 - y'^2 = 2. \]

Thus the equation of the rotated hyperbola is $x^2 - y^2 = 2$.

Exercise 35

Take the graph $y = e^x$. Consider either translating it $k$ units to the left, or dilating it by $e^k$ from the $x$-axis. Show that either transformation yields the same graph.

Exercise 36

The unit circle $x^2 + y^2 = 1$ is dilated by a factor of $2$ from the $x$-axis, then rotated by $\pi/4$ about the origin. What sort of curve results? What is its equation?

Exercise 37

Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a bijective function. Show that after reflection in the line $y=x$, the graph of $y=f(x)$ is sent to the graph of $y = f^{-1}(x)$.

Next page - Links Forward - Areas and determinants