Content
Describing geometric transformations algebraically
We have now seen several geometric plane transformations. We have also seen how matrices can describe some transformations (linear ones) in a simple algebraic way.
We now investigate these geometric operations from an algebraic point of view. We ask whether, and how, they can be represented by matrices. This gives us a very interesting way to relate everyday geometric operations to algebra.
Rotations
To everything — turn, turn, turn
— Pete Seeger
As discussed previously, given a point $P$ in the plane, and an angle $\phi$, we can consider the rotation around $P$ by angle $\phi$. By convention, we measure angles anticlockwise and in radians. We denote3 this rotation by
\[ \text{Rot}_{P, \; \phi} \; : \; \mathbb{R}^2 \rightarrow \mathbb{R}^2. \]Note the following preliminary facts about rotations:
- A rotation by angle $0$ is just the identity transformation, as is rotation by $2\pi$.
- Rotation by $\phi + 2\pi$ is the same transformation as rotation by $\phi$.
- Rotations of angles $\theta$ and $\phi$ about the same point $P$ give a rotation of $\theta + \phi$ about $P$.
- Any rotation is bijective. Indeed, a rotation by $\phi$ about $P$ can be undone by rotating by $-\phi$, so the transformation $\text{Rot}_{P, \; \phi}$ has inverse $\text{Rot}_{P, \; -\phi}$.
That is,
\[ \text{Rot}_{P, \; 0} = \text{Rot}_{P, \; 2\pi} = I, \quad \text{Rot}_{P, \; \phi + 2\pi} = \text{Rot}_{P, \; \phi}, \] \[ \text{Rot}_{P, \; \phi} \circ \text{Rot}_{P, \; \theta} = \text{Rot}_{P, \; \theta + \phi}, \quad \left( \text{Rot}_{P, \; \phi} \right)^{-1} = \text{Rot}_{P, \; -\phi}. \]Exercise 8
Consider $\text{Rot}_{{\bf 0}, \; \pi/2}$, rotation about the origin by $\pi/2$. Show that $\text{Rot}_{{\bf 0}, \; \pi/2} (x,y) = (-y,x)$.
Now, when we rotate around the origin ${\bf 0}$, it turns out that $\text{Rot}_{{\bf 0}, \; \phi}$ is a linear transformation. We will show why this is true, and find the corresponding matrix.
To show that $\text{Rot}_{{\bf 0}, \; \phi}$ is linear, we will show that it satisfies the "distributive" laws
\[ \text{Rot}_{{\bf 0}, \phi} (c {\bf v}) = c \text{Rot}_{{\bf 0}, \phi} ({\bf v}) \quad \text{and} \quad \text{Rot}_{{\bf 0}, \phi} \left( {\bf v} + {\bf w} \right) = \text{Rot}_{{\bf 0}, \phi} \left( {\bf v} \right) + \text{Rot}_{{\bf 0}, \phi} \left( {\bf w} \right), \]for any vectors ${\bf v}, {\bf w}$ and real number $c$.
For the first law, note that the two vectors $c{\bf v}$ and ${\bf v}$ point in the same direction; $c{\bf v}$ is $c$ times longer than ${\bf v}$. After rotation by $\phi$ about ${\bf 0}$, the two resulting vectors still point in the same direction and one is still $c$ times longer than the other, so
\[ \text{Rot}_{{\bf 0}, \phi} \left( c {\bf v} \right) = c \text{Rot}_{{\bf 0},\phi} ( {\bf v} ) \quad \text{as desired}. \]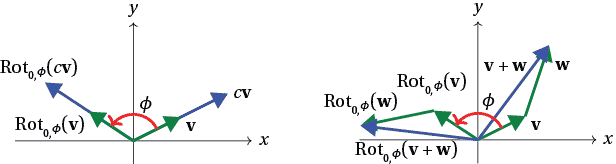
For the second law, place ${\bf v}$ at the origin and place ${\bf w}$ head-to-tail with it, as shown, to obtain the vector ${\bf v} + {\bf w}$. After rotating these vectors all by $\phi$, we have head-to-tail vectors $\text{Rot}_{{\bf 0}, \; \phi} ({\bf v})$ and $\text{Rot}_{{\bf 0}, \; \phi} ({\bf w})$, summing to $\text{Rot}_{{\bf 0}, \; \phi} ({\bf v} + {\bf w})$. Thus
\[ \text{Rot}_{{\bf 0}, \; \phi} ({\bf v}) + \text{Rot}_{{\bf 0}, \; \phi} ({\bf w}) = \text{Rot}_{{\bf 0}, \; \phi} ( {\bf v} + {\bf w} ) \quad \text{as desired}. \]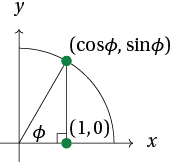
Now that we know $\text{Rot}_{{\bf 0}, \; \phi}$ is a linear transformation, we know that it corresponds to a matrix: the next question is to find the matrix.
To find the matrix, consider where the standard basis vectors $(1,0)$ and $(0,1)$ go under the rotation: this will give us the two columns of the matrix, as discussed earlier.
Rotating $(1,0)$ by an angle of $\phi$ about the origin, we obtain the point $(\cos \phi, \sin \phi)$, by elementary trigonometry in the right-angle triangle shown.
Exercise 9
Show that rotating $(0,1)$ by $\phi$ about the origin yields the point $(-\sin \phi, \cos \phi)$.
Thus we have found the columns of the matrix of $\text{Rot}_{{\bf 0}, \; \phi}$. The matrix is
\[ \begin{bmatrix} \cos \phi & - \sin \phi \\ \sin \phi & \cos \phi \end{bmatrix}. \]Such a matrix is often called a rotation matrix with angle $\phi$.
Example
Check directly that the inverse of the rotation matrix with angle $\phi$ is the rotation matrix with angle $-\phi$. Hence verify algebraically that
$\left( \text{Rot}_{{\bf 0}, \; \phi} \right)^{-1} = \text{Rot}_{{\bf 0}, \; -\phi}$.Solution
The inverse or the rotation matrix with angle $\phi$ is
\[ \begin{bmatrix} \cos \phi & -\sin \phi \\ \sin \phi & \cos \phi \end{bmatrix}^{-1} = \frac{1}{\cos^2 \phi + \sin^2 \phi} \begin{bmatrix} \cos \phi & \sin \phi \\ - \sin \phi & \cos \phi \end{bmatrix} = \begin{bmatrix} \cos(-\phi) & -\sin(-\phi) \\ \sin(-\phi) & \cos(-\phi) \end{bmatrix}, \]which is the rotation matrix with angle $-\phi$. So the inverse of $\text{Rot}_{{\bf 0}, \; \phi}$ is $\text{Rot}_{{\bf 0}, \; -\phi}$.
Exercise 10
Show that the product of the rotation matrices with angles $\theta$ and $\phi$ is the rotation matrix with angle $\theta + \phi$. Hence verify algebraically that
$\text{Rot}_{{\bf 0}, \; \theta} \circ \text{Rot}_{{\bf 0}, \; \phi} = \text{Rot}_{{\bf 0}, \; \theta + \phi}$.The formula for a rotation about the origin can also be derived directly. We can do this using polar coordinates. Instead of describing a point by its Cartesian coordinates $(x,y)$, we can use its distance from the origin $r$, and its direction $\theta$ from the origin. The angle $\theta$ is measured anticlockwise from the positive $x$-axis.
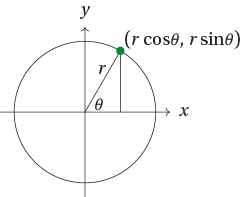
Basic trigonometry in the triangle shown gives $x = r \cos \theta$ and $y = r \sin \theta$. When we apply a rotation about the origin of angle $\phi$, the point $(x,y)$ moves an angle of $\phi$ around the origin, but its distance from the origin $r$ is unchanged. Hence the point $(x,y) = (r \cos \theta, r \sin \theta)$ is mapped to $(x',y') = (r \cos (\theta + \phi), r \sin (\theta + \phi) )$. We can now use the sine and cosine addition formulae to rewrite this expression:
\begin{align*} \text{Rot}_{{\bf 0}, \; \phi} \begin{bmatrix} x \\ y \end{bmatrix} &= \begin{bmatrix} r \cos (\theta + \phi) \\ r \sin (\theta + \phi) \end{bmatrix} = \begin{bmatrix} r \cos \theta \cos \phi - r \sin \theta \sin \phi \\ r \sin \theta \cos \phi + r \cos \theta \sin \phi \end{bmatrix} \\ &= \begin{bmatrix} (\cos \phi) x - (\sin \phi) y \\ (\sin \phi) x + (\cos \phi ) y \end{bmatrix} = \begin{bmatrix} \cos \phi & - \sin \phi \\ \sin \phi & \cos \phi \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}. \end{align*}This gives us a formula for $\text{Rot}_{{\bf 0}, \; \phi}$ and the rotation matrix directly.
While a rotation about the origin gives a linear transformation, a rotation about any other point is not linear, and hence is not given by a matrix. It is a plane transformation, but not a linear one. You can prove this in the next exercise.
Exercise 11
If $\phi$ is not a multiple of $2\pi$, and $P$ is not the origin, show that $\text{Rot}_{P, \; \phi} ({\bf 0}) \neq {\bf 0}$. Using exercise 2, conclude that $\text{Rot}_{P, \; \phi} ({\bf 0})$ is not linear.
In the section on Translations, you can find a formula for a rotation about any point.
Translations
I like to move it, move it
— Reel 2 Real4
Let ${\bf v} = (a,b)$. When we translate a point, with position vector ${\bf x} = (x,y)$, by ${\bf v}$, we simply add the two vectors, as shown below. Thus
\[ \text{Trans}_{{\bf v}} ({\bf x}) = {\bf x} + {\bf v}, \quad \text{or equivalently,} \quad \text{Trans}_{{\bf v}} (x,y) = (x+a, y+b). \]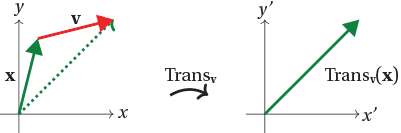
Translation by ${\bf 0}$ does not move points very far! It is the identity: $\text{Trans}_{{\bf 0}} = I$.
When ${\bf v} \neq {\bf 0}$, translation by ${\bf v}$ is not a linear transformation. The constant terms $a,b$ in the formula $(x+a,y+b)$ are not allowed under our definition of linear transformation. Another way to see that $\text{Trans}_{{\bf v}}$ is not linear is to note that $\text{Trans}_{{\bf v}} ({\bf 0}) = {\bf v}$, but a linear transformation must take the origin ${\bf 0}$ to ${\bf 0}$ (exercise 2). (Transformations which allow both linear and constant terms are called affine transformations.)
Exercise 12
Show that for any vector ${\bf v}$, the translation $\text{Trans}_{{\bf v}} : \mathbb{R}^2 \rightarrow \mathbb{R}^2$ is bijective. Find the inverse transformation, and give it an geometric interpretation.
Exercise 13
(This exercise may be easier after reading the rest of this module.)Let $P = (a,b)$ be a point in the plane with position vector ${\bf v}$.
Show that translation by $-{\bf v}$, followed by rotation by angle $\phi$ about the origin ${\bf 0}$, followed by translation by ${\bf v}$, gives the plane transformation which rotates by angle $\phi$ about $P$. That is, show that
\[ \text{Trans}_{{\bf v}} \circ \text{Rot}_{{\bf 0}, \; \phi} \circ \text{Trans}_{-{\bf v}} = \text{Rot}_{P, \; \phi}. \] Hence give a formula for $\text{Rot}_{P, \; \theta} (x,y)$, the rotation of $(x,y)$ by angle $\theta$ around $P = (a,b)$.Projections
As discussed earlier, given a line $L$ on the plane, we can consider the plane transformation which projects points onto $L$. We can denote6 this transformation by
\[ \text{Proj}_L \; : \; \mathbb{R}^2 \rightarrow \mathbb{R}^2. \]Such projections are very familiar from everyday life. If the plane is a map, $L$ is a road, and $P$ is your position, then $\text{Proj}_L (P)$ is the point on the road closest to you. If the line $L$ is horizontal, representing the ground, $P$ is above ground, and the sun is directly above, then $\text{Proj}_L (P)$ is the shadow of $P$ on the ground.
We have some preliminary facts about projections:
- A projection $\text{Proj}_L$ is not surjective. Its image consists only of points on $L$.
- A projection $\text{Proj}_L$ is not injective. Many points project to any given point of $L$.
- If $P$ is a point on $L$, then $\text{Proj}_L (P) = P$.
- After projecting a point onto $L$, projecting onto $L$ again has no further effect. That is, $\text{Proj}_L \circ \text{Proj}_L = \text{Proj}_L$.
A function $f$ such that $f \circ f = f$ is called an idempotent. The last property above says a projection is an idempotent.
Exercise 14
Give proofs of the above facts.
As it turns out, when the line $L$ passes through the origin, $\text{Proj}_L$ is a linear transformation. We will show why, and find the corresponding matrix.
First of all, suppose $L$ is the $x$-axis. Projection onto $L$ in this case just sets the $y$-coordinate of a point to $0$, and leaves the $x$-coordinate unchanged: $\text{Proj}_{\text{$x$-axis}} (x,y) = (x,0)$. Similarly $\text{Proj}_{\text{$y$-axis}} (x,y) = (0,y)$. These are linear transformations: \[ \text{Proj}_{\text{$x$-axis}} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x \\ 0 \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}, \quad \text{Proj}_{\text{$y$-axis}} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 \\ y \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}. \]Now suppose that $L$ is any line through the origin, making an angle of $\phi$ with the positive $x$-axis (as always, measured anticlockwise in radians), and let ${\bf v} = (x,y)$.
The key idea to calculate $\text{Proj}_L ({\bf v})$ is to perform the projection in several steps. We first rotate the plane by $-\phi$ about the origin. This rotates $L$ to the $x$-axis, and rotates ${\bf v}$ too. Then, we project onto the $x$-axis. Finally, we rotate back by $\phi$ around the origin. The result is that ${\bf v}$ has been projected onto $L$. In symbols,
\[ \text{Proj}_L = \text{Rot}_{{\bf 0}, \phi} \circ \text{Proj}_{\text{$x$-axis}} \circ \text{Rot}_{{\bf 0}, -\phi}. \]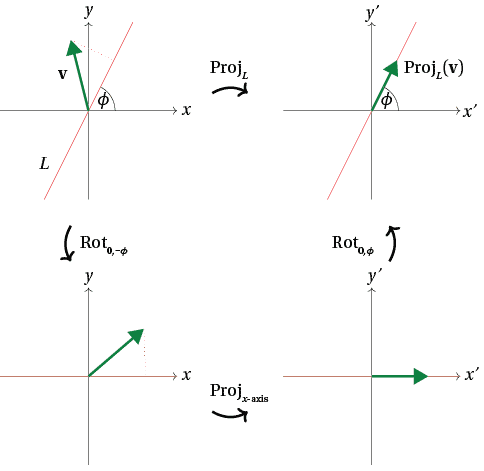
Why did we do this? Because we know all the matrices for the transformations on the right hand side! The matrix for $\text{Proj}_{\text{$x$-axis}}$ is given above, and
\[ \text{Rot}_{{\bf 0}, \phi} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} \cos \phi & - \sin \phi \\ \sin \phi & \cos \phi \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}, \quad \text{Rot}_{{\bf 0}, -\phi} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} \cos \phi & \sin \phi \\ - \sin \phi & \cos \phi \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}. \]Hence $\text{Proj}_L$ is linear, and its matrix is given by multiplying these matrices together:
\[ \begin{bmatrix} \cos \phi & - \sin \phi \\ \sin \phi & \cos \phi \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} \cos \phi & \sin \phi \\ - \sin \phi & \cos \phi \end{bmatrix} %&= \begin{bmatrix} \cos \phi & -\sin \phi \\ \sin \phi & \cos \phi \end{bmatrix} %\begin{bmatrix} \cos \phi & \sin \phi \\ 0 & 0 \end{bmatrix} \\ = \begin{bmatrix} \cos^2 \phi & \sin \phi \cos \phi \\ \sin \phi \cos \phi & \sin^2 \phi \end{bmatrix}. \]So projection onto $L$ is a linear transformation corresponding to this matrix:
\[ \text{Proj}_L \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} \cos^2 \phi & \sin \phi \cos \phi \\ \sin \phi \cos \phi & \sin^2 \phi \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} %= %\begin{bmatrix} x \cos^2 \phi + y \sin \phi \cos \phi \\ x \sin \phi \cos \phi + y \sin^2 \phi \end{bmatrix}. \]When $\phi = 0$, this matrix agrees with our calculation for projection onto the $x$-axis.
Example
Let $L$ be the line $y=x$. Find a formula for projection onto $L$.
Solution
The line $L$ passes through the origin and makes an angle $\phi = \pi/4$ with the positive $x$-axis. Hence $\text{Proj}_L$ is a linear transformation with matrix
\[ \begin{bmatrix} \cos^2 \frac{\pi}{4} & \sin \frac{\pi}{4} \cos \frac{\pi}{4} \\ \sin \frac{\pi}{4} \cos \frac{\pi}{4} & \sin^2 \frac{\pi}{4} \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{bmatrix}. \]Therefore,
\[ \text{Proj}_L \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} \frac{x+y}{2} \\ \frac{x+y}{2} \end{bmatrix}. \]Exercise 15
Verify the above formula for projection onto $y=x$ directly as follows.Given a point $(x_0, y_0)$, find the intersection of the line through this point with gradient $-1$, with the line $y=x$. Conclude that $\text{Proj}_L (x_0,y_0) = (\frac{x_0+y_0}{2}, \frac{x_0+y_0}{2})$ as above.
Exercise 16
What is the projection of the point $(8,3)$ onto the line $y=2x$?
An alternative derivation of the projection matrix is given in the following exercise.
Exercise 17
Let $L$ be a line through the origin, making an angle $\phi$ with the positive real axis.
- Show that $\text{Proj}_L (c{\bf v}) = c \text{Proj}_L ({\bf v})$ and $\text{Proj}_L ({\bf v} + {\bf w}) = \text{Proj}_L ({\bf v}) + \text{Proj}_L ({\bf w})$, for any vectors ${\bf v}, {\bf w}$ and real number $c$.
- Show that the projection of the point $(1,0)$ onto $L$ is $(\cos^2 \phi, \sin \phi \cos \phi)$, and the projection of $(0,1)$ onto $L$ is $(\sin \phi \cos \phi, \sin^2 \phi)$.
- Conclude that $\text{Proj}_L$ is as given above.
It's now possible to see some facts about projections from the algebraic properties of a projection matrix.
Exercise 18
Let $L$ be the line through the origin making an angle of $\phi$ with the positive $x$-axis.
- Let $P = (x,y)$ be a point on $L$. Show that \[ \begin{bmatrix} \cos^2 \phi & \sin \phi \cos \phi \\ \sin \phi \cos \phi & \sin^2 \phi \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x \\ y \end{bmatrix} \quad \text{and hence} \quad \text{Proj}_L (P) = P. \]
- Show that $\text{Proj}_L \circ \text{Proj}_L = \text{Proj}_L$ by demonstrating that \[ \begin{bmatrix} \cos^2 \phi & \sin \phi \cos \phi \\ \sin \phi \cos \phi & \sin^2 \phi \end{bmatrix}^2 = \begin{bmatrix} \cos^2 \phi & \sin \phi \cos \phi \\ \sin \phi \cos \phi & \sin^2 \phi \end{bmatrix}. \]
While projection onto a line through the origin is linear, projection onto a line not through the origin is not linear, and hence not given by a matrix, as you can prove now.
Exercise 19
If $L$ does not pass through the origin, show $\text{Proj}_L$ is not linear. (Hint: exercise 2.)
Reflections
As discussed earlier, given a line $L$ in the plane, we can consider the plane transformation which reflects points in $L$.We denote7 this transformation by
\[ \text{Ref}_L : \mathbb{R}^2 \rightarrow \mathbb{R}^2. \]Here are some elementary facts about reflections:
- Reflecting a point $P$ in $L$, and reflecting it in $L$ again, returns you to $P$. Hence, \[ \text{Ref}_L \circ \text{Ref}_L = I. \]
- A reflection is bijective; in fact, the inverse of a reflection is itself: \[ \left( \text{Ref}_L \right)^{-1} = \text{Ref}_L. \]
- In $P$ is a point on $L$, then its reflection in $L$ is just $P$ again; $\text{Ref}_L (P) = P$.
A function $f$ such that $f \circ f$ is the identity —- equivalently, a function which is its own inverse —- is called an involution. So reflections are involutions.
When $L$ is the $x$-axis, reflection in $L$ fixes the $x$-coordinate and "flips" the $y$-coordinate. Similarly, reflection in the $y$-axis "flips" the $x$-coordinate:
\[ \text{Ref}_{\text{$x$-axis}} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x \\ -y \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}, \quad \text{Ref}_{\text{$y$-axis}} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} -x \\ y \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}. \]So reflection in either axis is a linear transformation.
In fact, for any line $L$ passing through the origin, $\text{Ref}_L$ is a linear transformation. Letting $\phi$ be the angle between $L$ and the positive $x$-axis, the corresponding matrix is given by
\[ \text{Ref}_L \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} \cos (2\phi) & \sin (2\phi) \\ \sin (2\phi) & -\cos (2\phi) \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}. \]In the following two exercises, we outline two methods to derive this result, similar to those seen previously for projections.
Exercise 20
Show that rotation of angle $-\phi$ about the origin ${\bf 0}$, followed by reflection in the $x$-axis, followed by rotation of $\phi$ about ${\bf 0}$, is the same as reflection in $L$, i.e.
\[ \text{Ref}_L = \text{Rot}_{{\bf 0}, \phi} \circ \text{Ref}_{\text{$x$-axis}} \circ \text{Rot}_{{\bf 0}, -\phi}. \]Hence show that $\text{Ref}_L$ is a linear transformation and find its matrix.
Exercise 21
- Show that $\text{Ref}_L (c {\bf v}) = c \text{Ref}_L ({\bf v})$ and $\text{Ref}_L ( {\bf v} + {\bf w}) = \text{Ref}_L ({\bf v}) + \text{Ref}_L ({\bf w})$, for any vectors ${\bf v}$, ${\bf w}$ and real number $c$. Hence show $\text{Ref}_L$ is a linear transformation.
- Show that the reflection of the point $(1,0)$ in $L$ is $(\cos (2\phi), \sin (2\phi) )$, and that the reflection of $(0,1)$ in $L$ is $(\sin(2\phi), -\cos(2\phi))$.
- Hence find the matrix for $\text{Ref}_L$.
Reflection in one particular line $y=x$ has a useful effect: it swaps coordinates.
Example
Let $L$ be the line $y=x$. Show that reflection in $L$ takes a point $(x,y)$ to $(y,x)$.
Solution
Since $L$ passes through the origin with angle $\phi = \pi/4$, $\text{Ref}_L$ is linear, with matrix
\[ \begin{bmatrix} \cos \frac{\pi}{2} & \sin \frac{\pi}{2} \\ \sin \frac{\pi}{2} & - \cos \frac{\pi}{2} \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}. \]Thus
\[ \text{Ref}_L \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} y \\ x \end{bmatrix} \quad \text{as desired.} \]Exercise 22
Give a formula for reflection in the line $y=2x$.
The following exercise gives an interesting relationship between reflections and projections, and leads to a third way to derive the reflection matrix.
Exercise 23
Let $L$ be a line in the plane, and ${\bf x}$ a vector. Show that
\[ \text{Ref}_L ({\bf x}) = 2 \text{Proj}_L ({\bf x}) - {\bf x}, \quad \text{or equivalently,} \quad \text{Ref}_L = 2 \text{Proj}_L - I. \](Hint: Show ${\bf x} - \text{Proj}_L ({\bf x}) = - \left( \text{Ref}_L ({\bf x}) - \text{Proj}_L ({\bf x}) \right)$.)
(The above exercise holds for any line $L$ —- it need not pass through the origin!)
Exercise 24
Let $L$ be a line through the origin, making an angle of $\phi$ with the positive $x$-axis.Using the previous exercise, and the matrix for $\text{Proj}_L$, deduce the formula for $\text{Ref}_L$.
In the next exercise, we observe properties of reflections in the algebra of reflection matrices.
Exercise 25
Let $L$ be the line through the origin making an angle of $\phi$ with the positive $x$-axis.
- Let $P = (x,y)$ be a point on $L$. Show that \[ \begin{bmatrix} \cos(2\phi) & \sin(2\phi) \\ \sin(2\phi) & -\cos(2\phi) \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x \\ y \end{bmatrix} \quad \text{and hence} \quad \text{Ref}_L (P) = P. \]
- Show that \[ \begin{bmatrix} \cos (2\phi) & \sin (2\phi) \\ \sin(2\phi) & - \cos(2\phi) \end{bmatrix}^2 = \text{Id} \quad \text{and hence show} \quad \text{Ref}_L \circ \text{Ref}_L = I. \]
We have seen that reflection in a line passing through the origin is linear. But, as with projections, if $L$ does not pass through the origin, then $\text{Ref}_L$ is not linear.
Exercise 26
Let $d$ be a real number, and let $L$ be the line $x=d$. Show that $\text{Ref}_L (x,y) = (2d-x,y)$.
(Hint: This can be shown directly, or by finding the projection and using exercise 23.)
Dilations
[R]ound the neck of the bottle was a paper label, with the words "DRINK ME" beautifully printed on it in large letters...
Alice ventured to taste it, and finding it very nice, (it had, in fact, a sort of mixed flavour of cherry-tart, custard, pine-apple, roast turkey, toffee, and hot buttered toast,) she very soon finished it off...
"What a curious feeling!" said Alice; "I must be shutting up like a telescope."
And so it was indeed: she was now only ten inches high
— Lewis Carroll, Alice's Adventures in Wonderland
The plane transformation of a dilation has a similar effect to Alice's "DRINK ME" potion or "EAT ME" cake: it stretches or shrinks objects in the plane.
As discussed previously, given a line $L$ and a real number $k$, we can consider the dilation from $L$ by factor $k$. We write8 this transformation as
\[ \text{Dil}_{L,k} : \mathbb{R}^2 \rightarrow \mathbb{R}^2. \]The effect of such a dilation is to stretch lengths by a factor of $k$ in the direction perpendicular to $L$. If $k$ is negative, then points are flipped to the other side of $L$.
Here are some basic properties of dilations:
- Dilating from $L$ with factor $m$, and then $k$, gives a dilation from $L$ with factor $km$. \[ \text{Dil}_{L,k} \circ \text{Dil}_{L,m} = \text{Dil}_{L,km} \]
- If $k \neq 0$, then dilation from $L$ with factor $k$ is bijective. Its inverse is given by dilation from $L$ with factor $1/k$. \[ \left( \text{Dil}_{L,k} \right)^{-1} = \text{Dil}_{L, \frac{1}{k}} \]
- If $P$ is a point on $L$, then for any $k$, $\text{Dil}_{L,k} (P) = P$.
These facts are true even for dilation by negative factors.
We will analyse dilations similarly to projections and reflections. First, dilation from the $x$-axis with factor $k$ leaves the $x$-coordinate unchanged, and multiplies the $y$-coordinate by $k$: $\text{Dil}_{\text{$x$-axis},k} (x,y) = (x,ky)$. Similarly for the $y$-axis, $\text{Dil}_{\text{$y$-axis},k} (x,y) = (kx,y)$. Hence
\[ \text{Dil}_{\text{$x$-axis},k} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} x \\ ky \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & k \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}, \quad \text{Dil}_{\text{$y$-axis},k} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} kx \\ y \end{bmatrix} = \begin{bmatrix} k & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}. \]Thus a dilation from either axis is a linear transformation.
In fact, for any line $L$ passing through the origin and any real $k$, $\text{Dil}_{L,k}$ is a linear transformation. Letting $\phi$ denote the angle $L$ makes with the positive $x$-axis, we have
\[ \text{Dil}_{L,k} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 1 + (k-1) \sin^2 \phi & (1-k) \sin \phi \cos \phi \\ (1-k) \sin \phi \cos \phi & 1 + (k-1) \cos^2 \phi \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}. \]You can check that $\phi = 0$ or $\pi/2$ gives the matrices above for dilations in the axes.
Exercise 27
- Show that $\text{Dil}_{L,k} = \text{Rot}_{{\bf 0}, \phi} \circ \text{Dil}_{\text{$x$-axis},k} \circ \text{Rot}_{{\bf 0}, -\phi}$.
- Hence show that $\text{Dil}_{L,k}$ is a linear transformation, with matrix as claimed above.
Example
Find a formula for dilation from the line $y=-x$ with factor $3$.
Solution
This line $L$ has angle $\phi = -\pi/4$, so $\sin \phi = \frac{-1}{\sqrt{2}}$ and $\cos \phi = \frac{1}{\sqrt{2}}$. Hence
\[ \begin{bmatrix} 1 + (k-1) \sin^2 \phi & (1-k) \sin \phi \cos \phi \\ (1-k) \sin \phi \cos \phi & 1 + (k-1) \cos^2 \phi \end{bmatrix} = \begin{bmatrix} 1 + 2 \cdot \frac{1}{2} & -2 \cdot \frac{-1}{2} \\ -2 \cdot \frac{-1}{2} & 1 + 2 \cdot \frac{1}{2} \end{bmatrix} = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix}, \]so the dilation is given by $\text{Dil}_{L,3} (x,y) = (2x+y,x+2y)$.
Exercise 28
What is the dilation of the point $(3,0)$ from the line $y=2x$ by factor $5$?
Dilation matrices are more complicated than rotation, reflection or projection matrices. Nonetheless, geometric properties of dilations are reflected in the algebra of dilation matrices.
Exercise 29
Suppose $k \neq 0$ and $L$ passes through the origin. Show that the matrices for dilation with factor $k$ and $\frac{1}{k}$ from $L$ are inverses. Hence conclude that $\left( \text{Dil}_{L,k} \right)^{-1} = \text{Dil}_{L, \frac{1}{k}}$.
Now for some particular values of $k$, dilation from a line $L$ by factor $k$ reduces to some transformations we have seen previously.
- Dilation from $L$ with factor $k=-1$ flips every point to the corresponding point on the opposite side of $L$: it is reflection in $L$.
- Dilation from $L$ with factor $k=0$ is just projection onto $L$. "Stretching from $L$ by factor zero" simply projects points onto $L$.
- Dilation from $L$ with factor $k=1$ leaves every point where it is.
In this sense, dilations form a generalisation of reflections and projections. We have
\[ \text{Dil}_{L,0} = \text{Proj}_L, \quad \text{Dil}_{L,-1} = \text{Ref}_L, \quad \text{Dil}_{L,1} = I. \]Exercise 30
- Show that a dilation matrix with $k=0$ is a projection matrix.
- Show that a dilation matrix with $k=-1$ is a reflection matrix.
Exercise 31
Use the fact that $\text{Dil}_{L,k} \circ \text{Dil}_{L,m} = \text{Dil}_{L,km}$ to show the following.
- A reflection is an involution, i.e. $\left( \text{Ref}_L \right)^2 = I$.
- A projection is an idempotent, i.e. $\left( \text{Proj}_L \right)^2 = \text{Proj}_L$.
Exercise 32
We can characterise dilation, projection and reflection matrices as follows. Let $M = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$. Show that the linear transformation corresponding to $M$ is:
- a projection onto a line if and only if $M$ is symmetric (i.e. $M$ equals its transpose $M^T$), $ad-bc = 0$, and $a+d=1$;
- a reflection in a line if and only if $M$ is symmetric, $a+d = 0$, and $ad-bc = -1$;
- a dilation if and only if $M$ is symmetric and $a+d = 1 + ad - bc$.
Spiral symmetries
A spiral symmetry is another interesting type of plane transformation. The spiral symmetry about a point $P$ with factor $r$ and angle $\theta$ is given by by dilating the whole plane by a factor $r$ from $P$, followed by a rotation by $\theta$ around $P$.
A spiral symmetry about the origin thus dilates a point $(x,y)$ to $(rx,ry)$ and then rotates it by $\theta$, to give the result
\[ \begin{bmatrix} \cos \theta & - \sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} rx \\ ry \end{bmatrix} = \begin{bmatrix} rx \cos \theta - ry \sin \theta \\ rx \sin \theta + ry \cos \theta \end{bmatrix} = \begin{bmatrix} r\cos \theta & - r \sin \theta \\ r \sin \theta & r \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}. \]Example
Let $M = \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix}$. Describe the linear transformation $T_M$ geometrically.
Solution
Form the parallelogram spanned by $T_M (1,0) = (1,1)$ and $T_M(0,1) = (-1,1)$, and view $T_M$ as in previous examples. We see $T_M$ sends the unit square to a square of side length $\sqrt{2}$, rotated by $\pi/4$.
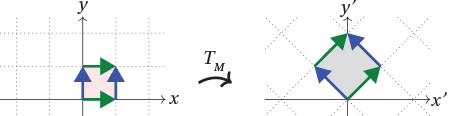
Thus $T_M$ is a spiral symmetry about the origin with factor $r=\sqrt{2}$ and angle $\theta = \pi/4$; indeed, $M$ agrees with the matrix above for these values of $r$ and $\theta$:
\[ M = \begin{bmatrix} 1 & -1 \\ 1 & 1 \end{bmatrix} = \begin{bmatrix} \sqrt{2} \cos \frac{\pi}{4} & -\sqrt{2} \sin \frac{\pi}{4} \\ \sqrt{2} \sin \frac{\pi}{4} & \sqrt{2} \cos \frac{\pi}{4} \end{bmatrix} = \begin{bmatrix} r \cos \theta & -r \sin \theta \\ r \sin \theta & r \cos \theta \end{bmatrix}. \]One reason spiral symmetries are interesting is because they arise naturally with complex numbers. Consider a complex number $w $ in polar form $w = r \; \text{cis} \theta = r (\cos \theta + i \sin \theta)$, where $r = |w|$ and $\theta = \arg w$. As the complex numbers form the Argand plane $\mathbb{C} \cong \mathbb{R}^2$, we may regard multiplication by $w$ as a plane transformation $\text{Mult}_w : \mathbb{R}^2 \rightarrow \mathbb{R}^2$, given by $\text{Mult}_w (z) = wz$. That is, $\text{Mult}_w$ multiplies complex numbers by $w$. If $z = x+yi$ then
\[ wz = r (\cos \theta + i \sin \theta) (x+yi) = \left( rx \cos \theta - ry \sin \theta \right) + i \left( rx \sin \theta + ry \cos \theta \right). \]If we write out the real and imaginary parts as components of a vector, this means
\[ \text{Mult}_w \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} rx \cos \theta - ry \sin \theta \\ rx \sin \theta + ry \cos \theta \end{bmatrix} = \begin{bmatrix} r \cos \theta & - r \sin \theta \\ r \sin \theta & r \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}. \]This is exactly a spiral symmetry! Hence, the effect of multiplication by a complex number $w$ on the complex plane is a spiral symmetry about the origin $0$ with factor $|w|$ and angle $\arg \theta$.
3Please note: This is not a standard notation. We find it useful, but it may not be used by others!
4Not to be confused with $\mathbb{R} \rightarrow \mathbb{R}$!
5Again, this is not a standard notation
6Again, beware that this notation is not standard.
7Again, notation not standard.
8Again, not a standard notation.
