Content
A walking problem
In the early eighteenth century the city of Königsberg was in Prussia. The city neatly straddled the River Pregel in which two large islands were connected to each other, and to the two banks of the river, by seven bridges (see Figure 3). The middle classes of the period created a problem for themselves. They wanted to start at some point of the city and walk over each bridge once and only once. But there was an extra condition. They also wanted to end up at the point where they had started.
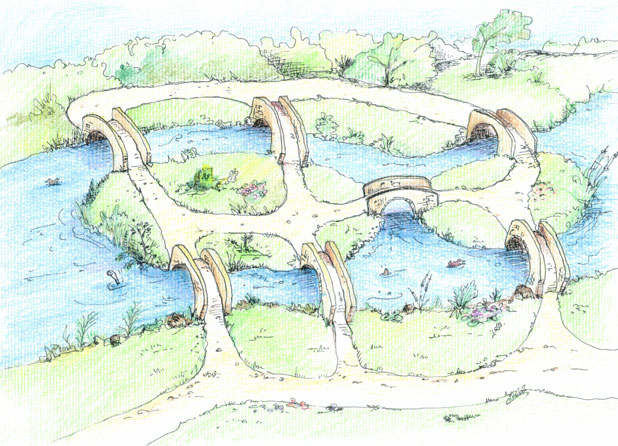
Figure 3: The bridges of Königsberg
Questions
- Were the fair people of Königsberg successful in walking over all the bridges once and getting back to where they started? (Model the situation using dots and lines joining them.)
- Could the bridge walk be achieved if the walkers were content not to return to their starting point?
- Can the round trip walk be achieved if one or more of the bridges were removed?
- Think of a city with seven bridges arranged in some other way. Is it possible for the round trip walk to be made successfully? (Move towards a generalisation of the Königsberg problem.)
- Repeat the last question with eight, nine and ten bridges. What can be said about the land masses in each case?
- Is there a general result here that covers any number of bridges? What do you need to know about the way that the bridges are connected to the land masses?
The Königsberg Bridge Problem was solved by the Swiss mathematician Leonhard Euler (pronounced `Oiler ') in 1736. It heralded the start of the study of two new areas of mathematics, graph theory and topology.
For more details see https://en.wikipedia.org/wiki/Seven_Bridges_of_Königsberg.
There are many situations that can be modelled using this simple dot and line model. You might think of the route maps found in various in-flight magazines, for example. But search out others. Look for social network situations, electrical networks, molecules or anything else that might use dots joined by lines.
Questions
- Gas, electricity and water from three different sources in the street are to be connected to three different inlets in a new house. Can this be done underground so that no two of the connections cross in any way?
