Content

Average velocity and average speed

Before turning our attention to problems involving non-constant acceleration and using calculus, we consider the concept of average velocity. We will look at examples involving motion with constant acceleration.

Average velocity

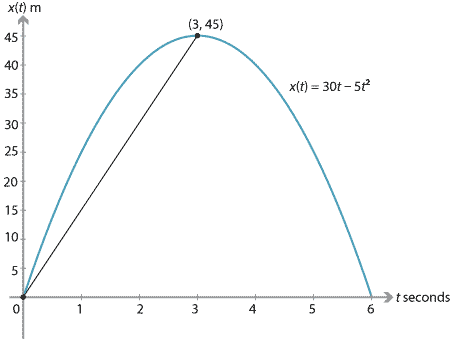
We return to the example of the stone being launched vertically upwards from ground level with an initial velocity of 30 m/s. The acceleration is taken as \(-10\) m/s\(^2\). We found that the stone's velocity is 0 m/s after three seconds, when it is at a height of 45 metres. The average velocity for the first three seconds of motion is

\[ \dfrac{x(3)-x(0)}{3-0} = \dfrac{45}{3} = 15 \text{ m/s}. \]

This can be illustrated on the position–time graph by the chord from the origin to the point \((3,45)\). The gradient of this chord is 15.

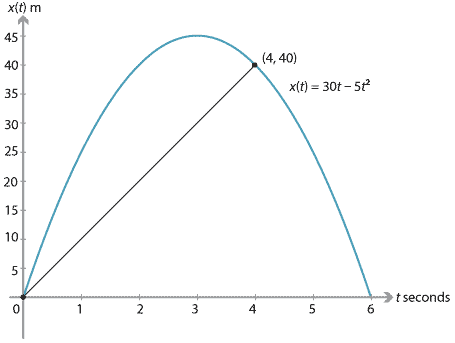
After a further second, the height (position) of the stone is 40 m. That is, \(x(4) = 40\). The average velocity for the first four seconds is

\[ \dfrac{x(4)-x(0)}{4-0} = \dfrac{40}{4} = 10 \text{ m/s}. \]

This can be illustrated by the chord from the origin to the point \((4,40)\). This chord has gradient 10.

The average velocity from the time the stone reaches its highest point to when the total time elapsed is 5 seconds is

\[ \dfrac{x(5)-x(3)}{5-3} = \dfrac{25-45}{2} = -10 \text{ m/s}. \]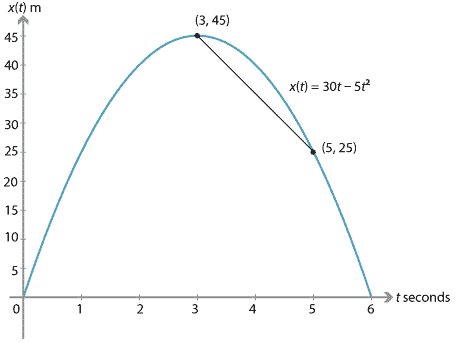

The average velocity from the time the stone is launched to the time it returns to ground level is

\[ \dfrac{x(6)-x(0)}{6-0} = 0 \text{ m/s}. \]

In general, we can write

\[ \text{Average velocity} = \dfrac{x(t_2)-x(t_1)}{t_2-t_1}, \]

where \(x(t_i)\) is the position of the particle at time \(t_i\).

Average speed

The average speed is the distance travelled divided by the time taken:

\[ \text{Average speed} = \dfrac{\text{Distance travelled}}{\text{Time taken}}. \]

Returning to the example of the stone launched upwards with initial velocity 30 m/s:

Next page - Content - Differential calculus and motion in a straight line