Answers to exercises
Exercise 1
\(\lim\limits_{x\to 0} \dfrac{\tan x}{x} = \lim\limits_{x\to 0}\Bigl(\dfrac{\sin x}{x}\times \dfrac{1}{\cos x}\Bigr) = 1\times 1 = 1\).Exercise 2
\(\lim\limits_{x\to 0} \dfrac{\sin 3x+\sin 7x}{5x} = \lim\limits_{x\to 0} \Bigl(\dfrac{3}{5}\times\dfrac{\sin 3x}{3x}\Bigr) + \lim\limits_{x\to 0} \Bigl(\dfrac{7}{5}\times\dfrac{\sin 7x}{7x}\Bigr) = \dfrac{3}{5}+\dfrac{7}{5} = 2\).Exercise 3
- Multiplying top and bottom by \(1+\cos x\) gives \[ \lim_{x\to 0} \dfrac{1-\cos x}{x^2} = \lim_{x\to 0} \dfrac{\sin^2x}{x^2(1+\cos x)} = \Bigl(\lim_{x\to 0}\dfrac{\sin x}{x}\Bigr)^2 \times \Bigl(\lim_{x\to 0} \dfrac{1}{1+\cos x}\Bigr) = \dfrac{1}{2}. \]
- Hence, for small \(x\), we have \[ \dfrac{1-\cos x}{x^2} \approx \dfrac{1}{2}, \] and so \(\cos x \approx 1-\dfrac{1}{2}x^2\).
Exercise 4
- We use two compound-angle formulas: \begin{align*} \cos(A-B) &= \cos A\,\cos B + \sin A\,\sin B \\ \cos(A+B) &= \cos A\,\cos B - \sin A\,\sin B. \end{align*} Let \(C=A+B\) and \(D=A-B\). Then \(A=\dfrac{1}{2}(C+D)\) and \(B=\dfrac{1}{2}(C-D)\). So it follows that \[ \cos C - \cos D = -2\,\sin A\,\sin B = -2\,\sin\Bigl(\dfrac{C+D}{2}\Bigr)\,\sin\Bigl(\dfrac{C-D}{2}\Bigr). \]
- \begin{align*} \dfrac{d}{dx} (\cos x) &= \lim_{h\to 0} \dfrac{\cos(x+h)-\cos x}{h} \\ &= \lim_{h\to 0} \dfrac{-2\,\sin(x+\dfrac{h}{2})\,\sin\dfrac{h}{2}}{h} \\ &= -\Bigl(\lim_{h\to 0} \,\sin\bigl(x+\dfrac{h}{2}\bigr)\Bigr) \times \Bigl(\lim_{h\to 0} \dfrac{\sin\dfrac{h}{2}}{\dfrac{h}{2}}\Bigr) = -\sin x. \end{align*}
Exercise 5
\(\dfrac{d}{dx}(\tan x) = \dfrac{d}{dx}\Bigl( \dfrac{\sin x}{\cos x} \Bigr) = \dfrac{\cos^2x +\sin^2x}{\cos^2x} = \dfrac{1}{\cos^2 x} = \sec^2 x\).Exercise 6
- \(\dfrac{d}{dx} (\operatorname{cosec} x) = \dfrac{d}{dx}(\sin x)^{-1} = -1(\sin x)^{-2} \times \cos x = -\dfrac{\cos x}{\sin^2 x} = -\operatorname{cosec} x\,\cot x\).
- \(\dfrac{d}{dx} (\sec x) = \dfrac{d}{dx}(\cos x)^{-1} = -1(\cos x)^{-2}\times -\sin x = \dfrac{\sin x}{\cos^2 x} = \tan x\,\sec x\).
- \(\dfrac{d}{dx} (\cot x) = \dfrac{d}{dx}\Bigl(\dfrac{\cos x}{\sin x}\Bigr) = \dfrac{-\sin^2x-\cos^2x}{\sin^2x}= -\operatorname{cosec}^2 x\).
Exercise 7
\begin{align*} \dfrac{d}{dx} \log_e\Bigl(\dfrac{1+\sin x}{\cos x}\Bigr) &= \dfrac{d}{dx}\bigl(\log_e(1+\sin x) - \log_e(\cos x)\bigr) \\ &= \dfrac{\cos x}{1+\sin x} + \dfrac{\sin x}{\cos x} = \dfrac{\cos^2x + \sin^2x + \sin x}{(1+\sin x)\,\cos x} \\ &= \dfrac{1+\sin x}{(1+\sin x)\,\cos x} = \dfrac{1}{\cos x} = \sec x. \end{align*}Exercise 8
The derivative of the function is
\[ \dfrac{dy}{dx} = \dfrac{d}{dx} \Bigl(\dfrac{\sin x}{3+4\cos x}\Bigr) = \dfrac{3\cos x + 4}{(3+4\cos x)^2}. \]Since \(\cos x \geq -1\), it follows that \(\dfrac{dy}{dx} > 0\) whenever \(3 + 4\cos x \neq 0\). Hence, \(y\) is an increasing function wherever it is defined.
Exercise 9
The perimeter of the triangle is \(P = 2a + 2a\cos \theta = 2a(1+\cos\theta)\), so
\[ a = \dfrac{P}{2(1+\cos\theta)}. \]The area of the triangle is
\[ A = \dfrac{1}{2}\,\bigl(2a\cos \theta\bigr)\,\bigl(a\,\sin \theta\bigr) = a^2\cos\theta\,\sin\theta = \dfrac{1}{2}a^2\sin 2\theta. \]Substituting for \(a\) gives
\[ A = \dfrac{P^2\sin2\theta}{8(1+\cos\theta)^2}. \]We want to find \(\theta\) in the range 0 to \(\dfrac{\pi}{2}\) such that \(\dfrac{dA}{d\theta} = 0\). By the quotient rule, if \(\dfrac{dA}{d\theta} = 0\), then
\[ 16P^2\cos2\theta\,(1+\cos\theta)^2 + 16P^2\sin2\theta\,(1 + \cos\theta)\,\sin\theta = 0. \]It follows after some calculation that \((1 + \cos\theta)^2(2\cos\theta - 1) = 0\). So \(\cos\theta = -1\) or \(\cos\theta = \dfrac{1}{2}\). Hence, for \(0 < \theta < \dfrac{\pi}{2}\), the only solution is \(\theta = \dfrac{\pi}{3}\). The triangle is equilateral.
Exercise 10
- \(\displaystyle \int_{\frac{\pi}{6}}^\frac{\pi}{3} (\sin 2x + \cos 3x)\, dx = \Bigl[-\dfrac{1}{2}\cos 2x + \dfrac{1}{3} \sin 3x \Bigr]_{\frac{\pi}{6}}^\frac{\pi}{3} = \dfrac{1}{6}\).
- We have \(\dfrac{d}{dx} (x\,\sin x) = \sin x + x\,\cos x\). Hence \[ \int_0^{\frac{\pi}{2}} x\,\cos x\, dx = \Bigl[x\,\sin x\Bigr]_{0}^\frac{\pi}{2} - \int_0^{\frac{\pi}{2}} \sin x\, dx = \dfrac{\pi}{2}-1. \]
- \(\displaystyle \int \tan^2 x\, dx = \int \bigl(\sec^2 x - 1\bigr)\, dx = \tan x - x + C\).
Exercise 11
We have \(\sin^2\theta = \dfrac{1}{2}(1-\cos 2\theta)\), and so
\[ \int \sin^2\theta\, d\theta = \dfrac{1}{2}\Bigl(\theta - \dfrac{1}{2}\sin 2\theta\Bigr) + C. \]Exercise 12
Since the period is \(\pi \sqrt{2}\), we have \(\dfrac{2\pi}{n} = \pi\sqrt{2}\), so \(n=\sqrt{2}\). The amplitude is \(C=2\). Hence, from \(v^2=n^2(C^2-x^2)\), when \(x=0\), \(v=\pm 2\sqrt{2}\). Thus the speed is \(2\sqrt{2}\) m/s.
Exercise 13
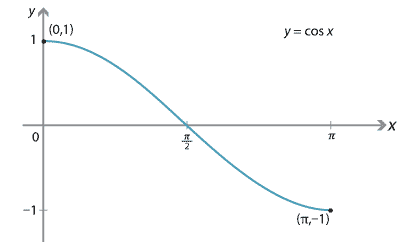
This restricted function has domain \([0,\pi]\) and range \([-1,1]\). So its inverse has domain \([-1,1]\) and range \([0,\pi]\).
Graphs of inverse cosine of minus x and minus inverse cosine of x showing one is a translation of the other.
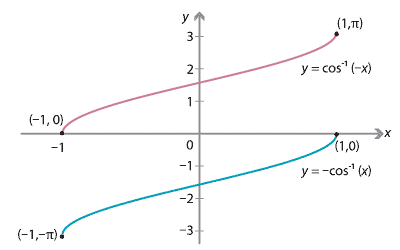
Detailed description
Since \(\cos \dfrac{\pi}{3} = \dfrac{1}{2}\), we have \(\cos^{-1}(\dfrac{1}{2}) = \dfrac{\pi}{3}\) and so \(\cos^{-1}(-\dfrac{1}{2}) = \pi - \cos^{-1}(\dfrac{1}{2}) = \pi - \dfrac{\pi}{3} = \dfrac{2\pi}{3}\).- Let \(y = \cos^{-1}x\). Then \(x = \cos y\), and so \[ \dfrac{dx}{dy} = -\sin y = -\sqrt{1 - \cos^2 y} = -\sqrt{1 - x^2}. \] (Note that \(0 \leq y \leq \pi\) and so \(0 \leq \sin y \leq 1\).) Hence, \[ \dfrac{dy}{dx} = -\dfrac{1}{\sqrt{1 - x^2}}. \]
- Let \(f(x) = \sin^{-1}x + \cos^{-1}x\), for \(x \in [-1, 1]\). Then \[ f'(x) = \dfrac{1}{\sqrt{1-x^2}}- \dfrac{1}{\sqrt{1-x^2}} = 0. \] So \(f(x) = C\), for some constant \(C\). Now \(f(0)=\dfrac{\pi}{2}\) and so \(\sin^{-1} x + \cos^{-1} x = \dfrac{\pi}{2}\).
