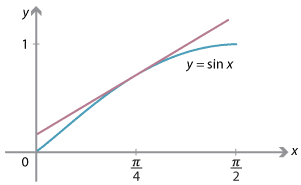Content

Differentiating trigonometric functions

The derivative of sine

Since the graph of \(y = \sin x\) is a smooth curve, we would like to find the gradient of the tangent to the curve at any point on it.

Before doing this, we derive a useful trigonometric identity that will assist us.

Using the compound-angle formulas, we have

\begin{align*} \sin(A+B) - \sin(A-B) &= \sin A\,\cos B + \cos A\,\sin B - (\sin A\,\cos B - \cos A\,\sin B) \\ &= 2\,\cos A\,\sin B. \end{align*} If we put \(C=A+B\) and \(D=A-B\), we can add these equations to obtain \(A=\dfrac{1}{2}(C+D)\) and subtract them to obtain \(B=\dfrac{1}{2}(C-D)\). Substituting these back, we obtain the sine difference formula: \[ \sin C - \sin D = 2\,\cos\Bigl(\dfrac{C+D}{2}\Bigr)\,\sin\Bigl(\dfrac{C-D}{2}\Bigr). \]

To find the derivative of \(\sin x\), we return to the first principles definition of the derivative of \(y=f(x)\):

\[ \dfrac{dy}{dx} = \lim_{h\to 0} \dfrac{f(x+h)-f(x)}{h}. \]

Substituting \(y=\sin x\), we have

\[ \dfrac{dy}{dx} = \lim_{h\to 0} \dfrac{\sin(x+h) - \sin x}{h}. \]

Applying the sine difference formula, we have

\[ \lim_{h\to 0} \dfrac{\sin(x+h) - \sin x}{h} = \lim_{h\to 0} \dfrac{2\,\cos\bigl(x+\dfrac{h}{2}\bigr)\,\sin\bigl(\dfrac{h}{2}\bigr)}{h}. \]

We can put \(u=\dfrac{h}{2}\). Then \(u\to 0\) as \(h\to 0\). So the limit becomes

\begin{align*} \dfrac{dy}{dx} &= \lim_{u\to 0} \dfrac{2\,\cos(x+u)\,\sin u}{2u} \\ &= \Bigl(\lim_{u\to 0} \cos(x+u)\Bigr) \times \Bigl(\lim_{u\to 0}\dfrac{\sin u}{u}\Bigr) \\ &= \cos x \times 1 \\ &= \cos x. \end{align*}

We can thus conclude that

\[ \dfrac{d}{dx} (\sin x) = \cos x. \]

This result is both simple and surprising, and students need to commit it to memory.

The derivation above involved a number of ingredients and is often difficult for students the first time through.

Derivatives of other trigonometric functions

Now that the derivative of sine is established, we can use the standard rules of calculus — the chain, product and quotient rules — to proceed.

Since \(\cos x = \sin\bigl(x + \dfrac{\pi}{2}\bigr)\), we can apply the chain rule to see that

\begin{align*} \dfrac{d}{dx} (\cos x) &= \dfrac{d}{dx} \Bigl( \sin\bigl(x + \dfrac{\pi}{2}\bigr)\Bigr) \\ &= \cos \bigl(x + \dfrac{\pi}{2}\bigr) \\ &= -\sin x. \end{align*}

Thus

\[ \dfrac{d}{dx}(\cos x) = -\sin x. \]

This is also a simple and surprising result that needs to be committed to memory.

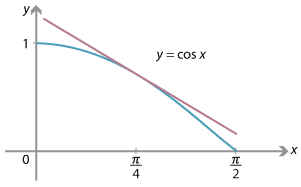
The following graphs illustrate what is happening geometrically. If we draw the tangent to the curve \(y=\sin x\) at a point with \(0 < x < \dfrac{\pi}{2}\), then the tangent clearly has positive gradient, while a tangent to \(y=\cos x\), in the same range, clearly has negative gradient.

Graph of y = sin x drawn for x greater than 0 and less than pi over two.
Detailed description

Graph of y = cos x drawn for x greater than 0 and less than pi over two.
Detailed description

The derivative of \(\cos x\) can also be found by using first principles.

Exercise 4

  1. Show that \[ \cos C - \cos D = -2\,\sin\Bigl(\dfrac{C+D}{2}\Bigr)\,\sin\Bigl(\dfrac{C-D}{2}\Bigr). \]
  2. Show by first principles that \[ \dfrac{d}{dx}(\cos x) = -\sin x. \]

Exercise 5

By writing \(\tan x = \dfrac{\sin x}{\cos x}\) and applying the quotient rule, prove that

\[ \dfrac{d}{dx} (\tan x) = \sec^2 x. \]

Students need to remember the derivatives of \(\sin\), \(\cos\) and \(\tan\).

The rules of calculus can also be used to find the derivatives of the reciprocal functions.

Exercise 6

Show that

  1. \(\dfrac{d}{dx} (\operatorname{cosec} x) = -\operatorname{cosec} x\,\cot x\)
  2. \(\dfrac{d}{dx} (\sec x) = \sec x\,\tan x\)
  3. \(\dfrac{d}{dx} (\cot x) = -\operatorname{cosec}^2 x\).

These three derivatives need not be committed to memory.

Further examples

Example

Use the rules of calculus to differentiate each of the following functions with respect to \(x\):

  1. \(4\,\sin(2x^2)\)
  2. \(x\,\cos(2x)\)
  3. \(e^{3x}\tan(4x)\).

Solution

  1. \(\dfrac{d}{dx}\bigl(4\,\sin(2x^2)\bigr) = 16x\,\cos(2x^2)\)
  2. \(\dfrac{d}{dx}\bigl(x\,\cos(2x)\bigr) = -2x\,\sin(2x)+\cos(2x)\)
  3. \(\dfrac{d}{dx}\bigl(e^{3x}\tan(4x)\bigr) = 4e^{3x}\sec^2(4x) + 3e^{3x}\tan(4x)\).

Exercise 7

Show that

\[ \dfrac{d}{dx} \log_e\Bigl(\dfrac{1+\sin x}{\cos x}\Bigr) = \sec x. \]

Next page - Content - Applications of the derivatives