Links forward

Integration and three dimensions

So far we have used integration to calculate areas, which are 2-dimensional. Integration can also be used to obtain 3-dimensional volumes.

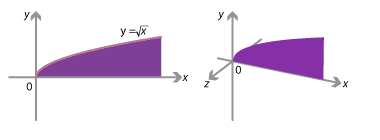
For instance, take a graph $y = f(x)$ in the $x–y$ plane, and consider adding a third dimension: points in 3-dimensional space have coordinates $(x,y,z)$, and there is now also a $z$-axis. The figures below show the graph of $y = \sqrt{x}$, for $0 \leq x \leq 5$, in the plane and then adding a $z$-axis.

Detailed description of diagrams

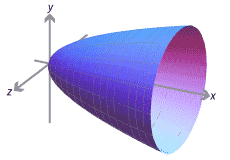
We can now consider rotating the curve around the $x$-axis. As we do, the curve sweeps out a surface, and the area under the curve sweeps out a 3-dimensional solid. The solid has rotational symmetry about the $x$-axis and is called a solid of revolution.

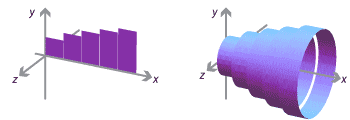
We can estimate the area under the graph $y=f(x)$ in the plane by subdividing the $x$-interval and forming rectangles. Rotating these rectangles about the $x$-axis, we estimate the volume of the solid of revolution by cylinders.

Detailed description of diagrams

Use our usual notation: we consider the graph of $y=f(x)$ between $x=a$ and $x=b$, and we divide the interval $[a,b]$ into $n$ subintervals $[x_0, x_1]$, $\dots$, $[x_{n-1}, x_n]$ of width $\Delta x$. As we have seen, for the right-endpoint estimate, the rectangles have width $\Delta x$ and height $f(x_j)$, and hence area $f(x_j) \; \Delta x$. Similarly, the cylinders have radius $f(x_j)$ and width $\Delta x$, and hence volume $\pi \, f(x_j)^2 \, \Delta x$. We can estimate the volume of the solid of revolution as $\sum_{j=1}^n \pi \, f(x_j)^2 \, \Delta x$. Taking the limit as $n \to \infty$, the volume of the solid of revolution is

$$\int_a^b \pi \, f(x)^2 \; dx.$$

More generally, if we have a solid bounded by the two parallel planes $x=a$ and $x=b$, and at each value of $x$ in $[a,b]$ the cross-sectional area of the solid is $A(x)$, then the volume of the solid is

$$\int_a^b A(x) \; dx.$$

Using this idea, it's possible to derive the formulas for the volumes of pyramids, prisms, and other solids. In higher mathematics courses one studies 3-dimensional (and higher-dimensional) volumes using multiple integrals.

Next page - Links forward - Arc length