Content

Calculating areas with antiderivatives

A general method to find the area under a graph \(y=f(x)\) between \(x=a\) and \(x=b\) is given by the following important theorem.

Theorem (Fundamental theorem of calculus)

Let \(f(x)\) be a continuous real-valued function on the interval \([a,b]\). Then

\[ \int_a^b f(x) \; dx = \Big[ F(x) \Big]_a^b = F(b) - F(a), \]

where \(F(x)\) is any antiderivative of \(f(x)\).

The notation \(\big[ F(x) \big]_a^b\) is just a shorthand to substitute \(x=a\) and \(x=b\) into \(F(x)\) and subtract; it is synonymous with \(F(b) - F(a)\).

Note that any antiderivative of \(f(x)\) will work in the above theorem. Indeed, if we have two different antiderivatives \(F(x)\) and \(G(x)\) of \(f(x)\), then they must differ by a constant, so \(G(x) = F(x) + c\) for some constant \(c\). Then we have to get the same answer whether we use \(F\) or \(G\), since

\begin{align*} G(b) - G(a) &= \big( F(b) + c \big) - \big( F(a) + c \big)\\ &= F(b) - F(a). \end{align*}

We give a proof of the theorem, assuming our previous statements:

the derivative of the area function is \(f(x)\)
any two antiderivatives of \(f(x)\) differ by a constant.

Proof

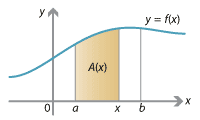
y = f(x) of f(x) = x squared + 1, parabola, region from x = 0 to point on x axis marked as x shaded between parabola and x axis, this area labelled as A(x).
Detailed description of diagram

As before, let \(A(c)\) be the area under the graph \(y=f(x)\) between \(x=a\) and \(x=c\). So we have an area function \(A(x)\) which measures the area between \(a\) and \(x\). We must find \(A(b)\), the area from \(a\) to \(b\). The derivative of the area function \(A(x)\) is \(f(x)\), so \(A(x)\) is an antiderivative of \(f(x)\). As both \(A(x)\) and \(F(x)\) are antiderivatives of \(f(x)\), they must differ by a constant, i.e., \(A(x) = F(x) + K\) for some constant \(K\). Since \(A(a) = 0\), this implies \(F(a) + K = 0\). Hence \(K = - F(a)\), and it follows that \(A(x) = F(x) - F(a)\). Therefore the desired integral is equal to \(A(b) = F(b) - F(a)\).
\(\Box\)

We can return to our original problem and solve it using the fundamental theorem.

Example

Find

\[ \int_0^5 (x^2 + 1) \; dx. \]

Solution

An antiderivative of \(x^2 + 1\) is \(\frac{1}{3} x^3 + x\), so we have

\begin{align*} \int_0^5 (x^2 + 1) \; dx &= \Bigg[ \frac{1}{3} x^3 + x \Bigg]_0^5\\ &= \Big( \frac{1}{3} \cdot 5^3 + 5 \Big) - \Big( \frac{1}{3} \cdot 0^3 + 0 \Big)\\ &= \frac{125}{3} + 5 = \frac{140}{3} = 46 \frac{2}{3}. \end{align*}

Exercise 10

Find

\[ \int_0^8 (3x^2 + \sqrt[3]{x}) \; dx. \]

Next page - Content - Velocity–time graphs