Content

Area and the antiderivative

Let's return to our function \(f(x) = x^2 + 1\), and our quest to find the area under the graph \(y=f(x)\) between \(x=0\) and \(x=5\), i.e.,

\[ \int_0^5 (x^2 + 1) \; dx. \]

As we've seen, we can estimate the area by many narrow rectangles, each over a subinterval of \([0,5]\), with width \(\Delta x\) and height given by a value of \(f(x)\). As we take the limit of more and more narrower and narrower rectangles, we get a better approximation to the area.

To calculate the exact area, we introduce an area function \(A\). For any fixed number \(c > 0\), let \(A(c)\) be the area under the graph \(y=f(x)\) between \(x=0\) and \(x=c\). So we can define the function \(A(x)\) to be the area between 0 and \(x\). Clearly \(A(0) = 0\). We seek \(A(5)\).

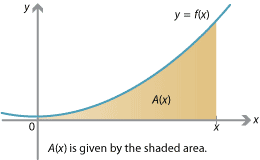
Detailed description of diagram

The fundamental idea is to consider the derivative of the area function \(A\). What is \(A'(x)\)?

In fact, \(A'(x) = f(x)\). We can see this geometrically. To differentiate \(A(x)\) from first principles, we consider

\[ \frac{A(x+h) - A(x)}{h}. \]

Now \(A(x+h)\) is the area under the graph up to \(x+h\), and \(A(x)\) is the area under the graph up to \(x\). Thus \(A(x+h) - A(x)\) is the area under the graph between \(x\) and \(x+h\).

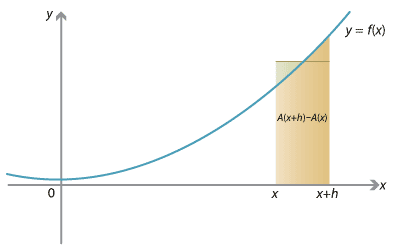
Detailed description of diagram

If you were to 'level off' the area under the graph between \(x\) and \(x+h\), you'd obtain a rectangle (as shown in the graph above) with width \(h\) and height equal to the average value of \(f\); dividing the area by \(h\) gives the average value:

\begin{align*} \frac{A(x+h)-A(x)}{h} &= \frac{\text{ area of rectangle }}{\text{ width of rectangle }} \\ &= \text{ height of rectangle } \\ &= \text{ average value of \(f\) over the interval \([x, x+h]\).} \end{align*}

If \(h\) becomes very small, then the interval \([x,x+h]\) approaches the single point \(x\). And the average value of \(f\) over this interval must approach \(f(x)\). So we have

\[ \lim_{h \to 0} \frac{A(x+h)-A(x)}{h} = f(x). \]

In other words,

\[ A'(x) = f(x), \]

and \(A(x)\) is an antiderivative of \(f(x)\).

Returning again to our example \(f(x) = x^2 + 1\), what then is the area function \(A(x)\)? Its derivative must be \(f(x) = x^2 + 1\). We're looking for a function \(A\) such that

\[ A'(x) = x^2 + 1 \qquad \text{and} \qquad A(0)= 0. \]

Thinking back to derivatives, we can see that the antiderivative

\[ A(x) = \frac{1}{3} x^3 + x \]

satisfies these criteria. Hence the total area is

\[ A(5) = \frac{125}{3} + 5 = \frac{140}{3} = 46 \frac{2}{3}, \]

confirming our earlier estimates. We can write this as

\[ \int_0^5 f(x) \; dx = A(5) - A(0) = \frac{140}{3}. \]

Next page - Content - Antiderivatives and indefinite integrals