Motivation

Adding up a function in small pieces

You ride your bicycle for 5 minutes. Your bike is equipped with a fancy speedometer, and you keep your eye on it — so you know precisely how fast you are going at every instant for those 5 minutes. How far did you go in those 5 minutes?

This is not a very realistic situation, but let's suspend disbelief for now and try to imagine how you might answer this question.

Detailed description of diagram

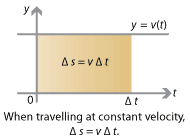
The first thing you recall is \(\Delta s = v \; \Delta t\). The change in your position, or displacement, \(\Delta s\) is given by your velocity \(v\) multiplied by the time taken \(\Delta t\). However, this equation only holds if you travel at constant velocity — but your speedometer said otherwise!

Trying to figure out how far you went on your bicycle, you recall how fast you were going at the 1-minute mark, at the 2-minute mark, and so on. Using this information and \(\Delta s = v \; \Delta t\), you estimate how far you went in each minute. Adding up these estimates, you have an estimate for how far you went over the whole 5 minutes.

But this might not be a very accurate estimate — your speed might change a lot over the course of a minute! What about all those hills in the third minute?

Trying to be more accurate, you break your trip down into 30-second intervals, and recall your speed after 30 seconds, 60 seconds, 90 seconds, and so on. Then you can estimate how far you went in each 30-second interval, and add them up to estimate the total distance you travelled. This may be more accurate than the previous estimate, but your speed still varies a lot over 30-second intervals.

Trying to be ever more accurate, you break your journey down into 10-second intervals ... then 5-second intervals ... then 1-second intervals ... and further. If you really knew your speed at every instant of the journey, you could perform all these calculations, and see how far you travelled. Your calculations would lead you to ever more accurate estimates of how far you really went. Your better and better estimates will approach, in the limit, the exact distance travelled. You might imagine in this limit that you were 'adding up your velocity at every instant' to give the precise answer.

Of course, this whole situation is wildly unrealistic.¹ However, in principle, we have given a mathematical technique to answer the question of how far you went. Given the function \(v(t)\), your velocity at time \(t\), you could use these ideas to calculate exactly how far you went. This idea of 'adding up' the function at more and more closer and closer points is essentially the idea of integration.

We've previously seen differentiation, and you might recall that differentiation can answer a related question. If you know where you are on your bike (i.e., your displacement) at every instant, then you can work out your velocity at every instant. If \(f(t)\) is how far you've travelled at time \(t\), then the derivative \(f'(t)\) gives your instantaneous velocity at time \(t\). This is the opposite problem: given position, we used differentiation to figure out velocity; now, given velocity, we use integration to figure out position.

It is an important fact that integrating a function — adding up the values over smaller and smaller intervals and seeing what the total is — turns out to be the opposite of differentiation. This is, as we will see, the idea of the fundamental theorem of calculus, the central idea of calculus.

Calculus is a crucial area of mathematics, necessary for understanding how quantities change in relation to each other, and for understanding almost every aspect of the physical world. Differentiation deals with how one quantity changes with respect to another, in the limit of small changes. But it is only half the story. Integration deals with the sum of these small changes, in the limit, adding them up and putting them back together again. Whether it's your speed on your bike, or biological populations, or chemical concentrations, or economic indicators, or environmental conditions, or physical phenomena — to understand how quantities in the world are related, we need to understand both differential and integral calculus.

Next page - Motivation and knowledge - Other questions