Example

An upturned cone with semivertical angle $45^\circ$ is being filled with water at a constant rate of 30 cm$^3$ per second.

When the depth of the water is 60 cm, find the rate at which

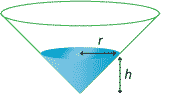
1. $h$, the depth of the water, is increasing
2. $r$, the radius of the surface of the water, is increasing
3. $S$, the area of the water surface, is increasing.

Solution

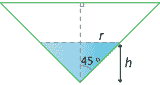
The volume $V$ of the water in the cone is given by

$$V = \dfrac{1}{3}\pi r^2h.$$

The cross-section of the cone is a right-angled isosceles triangle, and therefore $r = h$. Hence,

$$V = \dfrac{1}{3}\pi r^3 = \dfrac{1}{3}\pi h^3.$$

1. We seek $\dfrac{dh}{dt}$. Now $V = \dfrac{1}{3}\pi h^3$, and therefore $\dfrac{dV}{dh} =\pi h^2$. Hence, $$\begin{align*} \dfrac{dh}{dt} &= \dfrac{dh}{dV} \times \dfrac{dV}{dt} \\ &= \dfrac{1}{\pi h^2} \times 30 \\ &= \dfrac{30}{\pi h^2}. \end{align*}$$

   When $h = 60$, we have $\dfrac{dh}{dt} = \dfrac{1}{120\pi}$ cm/s.

2. We have seen that $r(t)=h(t)$. Thus, when $h = 60$, we have $\dfrac{dr}{dt} = \dfrac{1}{120\pi}$ cm/s.
3. We seek $\dfrac{dS}{dt}$. The area of the water's surface is $$S = \pi r^2.$$ Therefore $$\begin{align*} \dfrac{dS}{dt} &= \dfrac{dS}{dr} \times \dfrac{dr}{dt} \\ &= 2\pi r \times \dfrac{30}{\pi r^2} \\ &= \dfrac{60}{r}. \end{align*}$$

   When $h = 60$, we have $r = 60$, and so $\dfrac{dS}{dt} = 1$ cm$^2$/s.

Example

Variables $x$ and $y$ are related by the equation $y = 2 - \dfrac{4}{x}$. Given that $x$ and $y$ are functions of $t$ and that $\dfrac{dx}{dt} = 10$, find $\dfrac{dy}{dt}$ in terms of $x$.

Solution

If $y = 2 - \dfrac{4}{x}$, then $\dfrac{dy}{dx} =\dfrac{4}{x^2}$. Therefore $$\begin{align*} \dfrac{dy}{dt} &= \dfrac{dy}{dx}\times \dfrac{dx}{dt} \\ &= \dfrac{4}{x^2} \times 10 \\ &= \dfrac{40}{x^2}. \end{align*}$$

Example

A vessel of water is in the form of a frustum of a cone with semivertical angle $45^\circ$. The bottom circle of the vessel is a hole of radius $r$ cm. Water flows from this hole at a velocity of $c\sqrt{2gh}$ cm/s, where $c$ is a constant and $h$ cm is the height of the surface of the water above the hole.

1. Find the rate in cm$^3$/s at which water flows from the vessel.
2. Find the rate in cm/s at which $h$ is increasing.

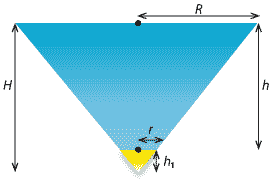
Solution

We first find the volume $V$ of water in the frustum. Consider removing a small cone from the 'tip' of a cone. This forms the hole. Let $H$ be the height of the larger cone (up to the water surface) and let $h_1$ be the height of the smaller cone (which is removed). Let $R$ be the radius of the larger cone and let $r$ be the radius of the smaller cone.

The height of the water is $h=H-h_1$. Therefore $$V = \dfrac{1}{3}\pi(R^2H-r^2h_1) = \dfrac{1}{3}\pi\bigl(R^2H - r^2(H-h)\bigr).$$ Because the semivertical angle is $45^\circ$, we have $R = H$ and $R-r = h$. Hence, $R = r + h$. Substituting for $R$ and $H$ in the equation for $V$, we have $$\begin{align*} V &= \dfrac{1}{3}\pi\bigl(R^2H - r^2(H-h)\bigr) \\ &= \dfrac{1}{3}\pi\bigl(R^3 - r^2(R-h)\bigr) \\ &= \dfrac{1}{3}\pi\bigl((r+h)^3 - r^3\bigr) \\ &= \dfrac{1}{3}\pi\bigl(3r^2h + 3rh^2 + h^3\bigr). \end{align*}$$

1. Let $v$ cm/s be the velocity of the flow of water from the hole at time $t$. We are given that $v = c\sqrt{2gh}$, where $h$ is the height of the water above the hole at time $t$. Since $$\dfrac{dV}{dt} = \text{area of the cross-section of the hole}\ \times\ \text{velocity of the flow of water from the hole},$$ we have $$\dfrac{dV}{dt} = \pi r^2 v = \pi r^2c \sqrt{2gh} \text{ cm}^3/\text{s}.$$
2. We found that the volume of water $V$ cm$^3$ is given by $$V = \dfrac{1}{3} \pi(3r^2h+3rh^2+h^3),$$ and so $$\dfrac{dV}{dh} = \pi (r+h)^2.$$ Using the chain rule, we have $$\dfrac{dh}{dt} = \dfrac{dh}{dV} \times \dfrac{dV}{dt} = \dfrac{cr^2\sqrt{2gh}}{(r+h)^2} \text{ cm/s}.$$