Links forward

Approximations of functions

We have seen that the equation of the tangent line to the graph \(y=f(x)\) at the point \(x=a\) is given by

\[ y = f(a) + f'(a)\,(x-a). \]

Therefore, if we define a linear function \(T_1 (x)\) as

\[ T_1(x) = f(a) + f'(a)\,(x-a), \]

then \(T_1(x)\) approximates \(f(x)\) near \(x=a\). In fact, since \(T'_1(x) = f'(a)\), we have

\[ T_1(a) = f(a) \qquad\text{and}\qquad T'_1(a) = f'(a). \]

So the functions \(T_1(x)\) and \(f(x)\) agree at \(x=a\), and their derivatives also agree at \(x=a\). In this sense, \(T_1(x)\) is the 'best linear approximation' to \(f(x)\) at \(x=a\).

However, there's no reason to stop at linear approximations: we might ask for the best quadratic approximation to \(f(x)\) at \(x=a\).

Consider the function

\[ T_2(x) = f(a) + f'(a)\,(x-a) + \dfrac{f''(a)}{2}\,(x-a)^2. \]

This is a quadratic function. Its derivatives are

\[ T'_2(x) = f'(a) + f''(a)\,(x-a) \qquad\text{and}\qquad T''_2(x) = f''(a), \]

so

\[ T_2(a) = f(a), \qquad T'_2(a) = f'(a) \qquad\text{and}\qquad T''_2(a) = f''(a). \]

That is, \(T_2(x)\) and \(f(x)\) agree at \(x=a\), as do their first and second derivatives. In this sense, \(T_2(x)\) is the best quadratic approximation to \(f(x)\) at \(x=a\).

In general, one can check that the function

\[ T_k (x) = f(a) + f'(a)\,(x-a) + \dfrac{f''(a)}{2!}\,(x-a)^2 + \dfrac{f^{(3)}(a)}{3!}\,(x-a)^3 + \dots + \dfrac{f^{(k)}(a)}{k!}\,(x-a)^k \]

is a polynomial of degree \(k\) which agrees with \(f(x)\) at \(x=a\), along with all its first \(k\) derivatives. That is,

\[ T_k (a) = f(a), \quad T'_k (a) = f'(a), \quad T''_k (a) = f''(a), \quad \dotsc, \quad T^{(k)}(a) = f^{(k)}(a). \]

In this sense, \(T_k (x)\) is the best polynomial approximation of degree \(k\) to \(f(x)\) at \(x=a\).

The polynomials \(T_k (x)\), called Taylor polynomials, are very important throughout mathematics and science for approximating functions. Taylor polynomials and their generalisations are studied extensively in university-level mathematics courses.

The following diagram shows some of the first few Taylor polynomials approximating the function \(f(x) = \sin x\) near \(x=0\). Note how they provide successively better approximations to \(f(x)\). (We will see how to differentiate \(\sin x\) in the module The calculus of trigonometric functions.)

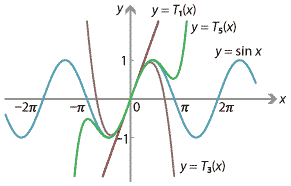
Figure : Taylor polynomials approximating \(\sin x\) at \(x=0\).

History and applications - The discoverers of calculus