Content

The gradient of secants and tangents to a graph

Consider a function \(f\colon \mathbb{R} \to \mathbb{R}\) and its graph \(y=f(x)\), which is a curve in the plane. We wish to find the gradient of this curve at a point. But first we need to define properly what we mean by the gradient of a curve at a point!

The module Coordinate geometry defines the gradient of a line in the plane: Given a non-vertical line and two points on it, the gradient is defined as \(\dfrac{\text{rise}}{\text{run}}\).

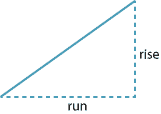
Figure : Gradient of a line.

Now, given a curve defined by \(y=f(x)\), and a point \(p\) on the curve, consider another point \(q\) on the curve near \(p\), and draw the line \(pq\) connecting \(p\) and \(q\). This line is called a secant line.

We write the coordinates of \(p\) as \((x,y)\), and the coordinates of \(q\) as \((x + \Delta x, y + \Delta y)\). Here \(\Delta x\) represents a small change in \(x\), and \(\Delta y\) represents the corresponding small change in \(y\).

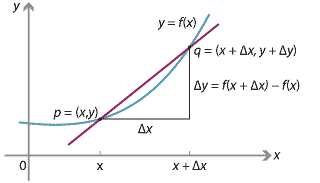
Figure : Secant connecting points on the graph \(y=f(x)\) at \(x\) and \(x+\Delta x\).

As \(\Delta x\) becomes smaller and smaller, the point \(q\) approaches \(p\), and the secant line \(pq\) approaches a line called the tangent to the curve at \(p\). We define the gradient of the curve at \(p\) to be the gradient of this tangent line.

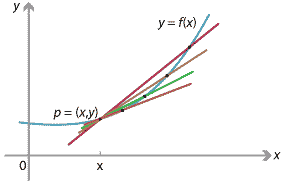
Detailed description
Figure : Secants on \(y=f(x)\) approaching the tangent line at \(x\).

Note that, in this definition, the approximation of a tangent line by secant lines is just like the approximation of instantaneous velocity by average velocities, as discussed in the Motivation section.

With this definition, we now consider how to compute the gradient of the curve \(y=f(x)\) at the point \(p = (x,y)\).

Taking \(q = (x + \Delta x, y + \Delta y)\) as above, the secant line \(pq\) has gradient

\[ \dfrac{\text{rise}}{\text{run}} = \dfrac{\Delta y}{\Delta x} = \dfrac{f(x+\Delta x) - f(x)}{\Delta x}. \]

Note that the symbol \(\Delta\) on its own has no meaning: \(\Delta x\) and \(\Delta y\) refer to change in \(x\) and \(y\), respectively. You cannot cancel the \(\Delta\)'s!

As \(\Delta x \to 0\), the gradient of the tangent line is given by

\[ \lim_{\Delta x \to 0} \dfrac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \dfrac{f(x+\Delta x) - f(x)}{\Delta x}. \]

We also denote this limit by \(\dfrac{dy}{dx}\):

\[ \lim_{\Delta x \to 0} \dfrac{\Delta y}{\Delta x} = \dfrac{dy}{dx}. \]

The notation \(\dfrac{dy}{dx}\) indicates the instantaneous rate of change of \(y\) with respect to \(x\), and is not a fraction. For our purposes, the expressions \(dx\) and \(dy\) have no meaning on their own, and the \(d\)'s do not cancel!

The gradient of a secant is analogous to average velocity, and the gradient of a tangent is analogous to instantaneous velocity. Velocity is the instantaneous rate of change of position with respect to time, and the gradient of a tangent to the graph \(y=f(x)\) is the instantaneous rate of change of \(y\) with respect to \(x\).

Next page - Content - Calculating the gradient of y = x²