Links forward

Finding limits using areas

One beautiful extension of the pinching theorem is to bound a limit using areas.

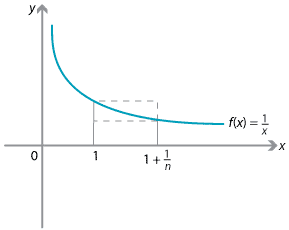
We begin by looking at the area under the curve \(y=\dfrac{1}{x}\) from \(x=1\) to \(x=1+\dfrac{1}{n}\).

The area under the curve is bounded above and below by areas of rectangles, so we have

\[ \dfrac{1}{n} \times \dfrac{1}{1+\dfrac{1}{n}}\leq \int_1^{1+\frac{1}{n}} \dfrac{1}{x}\, dx \leq \dfrac{1}{n} \times 1. \]

Hence

\[ \dfrac{1}{1+n} \leq \log_e\Bigl(1+\dfrac{1}{n}\Bigr) \leq \dfrac{1}{n}. \]

Now multiplying by \(n\), we have

\[ \dfrac{n}{1+n} \leq n\,\log_e\Bigl(1+\dfrac{1}{n}\Bigr) \leq 1. \]

Hence, if we take limits as \(n\to \infty,\) we conclude by the pinching theorem that

\begin{align*} n\log_e\Bigl(1+\dfrac{1}{n}\Bigr) \to 1 \ &\implies \ \log_e\bigl(1+\dfrac{1}{n}\Bigr)^n \to 1\\ &\implies \ \Bigl(1+\dfrac{1}{n}\Bigr)^n\to e \qquad (!!) \end{align*}

That is,

\[ \lim_{n\to \infty} \Bigl(1+\dfrac{1}{n}\Bigr)^n = e. \]

Next page - History and applications - Paradoxes of the infinite