Links forward
Formal definition of a limit
In this module, the notion of limit has been discussed in a fairly informal manner. To be able to prove results about limits and capture the concept logically, we need a formal definition of what we mean by a limit. We will only look here at the precise meaning of \(\lim\limits_{x\to \infty} f(x) = L\), but there is a similar definition for the limit at a point.
In words, the statement \(\lim\limits_{x\to \infty} f(x) = L\) says that \(f(x)\) gets (and stays) as close as we please to \(L\), provided we take sufficiently large \(x\). We now try to pin down this notion of closeness.
Another way of expressing the statement above is that, if we are given any small positive number \(\varepsilon\) (the Greek letter epsilon), then the distance between \(f(x)\) and \(L\) is less than \(\varepsilon\) provided we make \(x\) large enough. We can use absolute value to measure the distance between \(f(x)\) and \(L\) as \(|f(x) - L|\).
How large does \(x\) have to be? Well, that depends on how small \(\varepsilon\) is.
The formal definition of \(\lim\limits_{x\to \infty} f(x) = L\) is that, given any \(\varepsilon > 0\), there is a number \(M\) such that, if we take \(x\) to be larger than \(M\), then the distance \(|f(x) - L|\) is less than \(\varepsilon\).
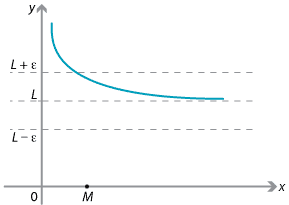
The value of \(f(x)\) stays within \(\varepsilon\) of \(L\) from the point \(x = M\) onwards.
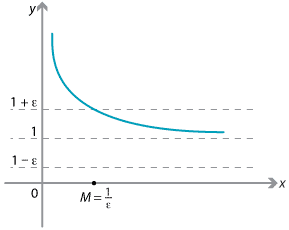
For example, consider the function \(f(x) = \dfrac{x+1}{x}\). We know from our basic work on limits that \(\displaystyle \lim_{x\to \infty} f(x) = 1\). For \(x > 0\), the distance is
\[ \bigl|f(x) - 1\bigr| = \Bigl|\dfrac{x+1}{x} - 1\Bigr| = \dfrac{1}{x}. \]So, given any positive real number \(\varepsilon\), we need to find a real number \(M\) such that, if \(x>M\), then \(\dfrac{1}{x} < \varepsilon\). For \(x>0\), this inequality can be rearranged to give \(x > \dfrac{1}{\varepsilon}\). Hence we can choose \(M\) to be \(\dfrac{1}{\varepsilon}\).
Exercise 8
Let \(f(x) = \dfrac{2x^2+3}{x^2}\). Given \(\varepsilon > 0\), find \(M\) such that if \(x>M\) we have \(|f(x)-2|< \varepsilon\). Conclude that \(f(x)\) has a limit of 2 as \(x\to \infty\).
While the formal definition can be difficult to apply in some instances, it does give a very precise framework in which mathematicians can properly analyse limits and be certain about what they are doing.
