Answers to exercises

Exercise 1

Coordinates of \(P\)	\(\theta\)	\(\sin\theta\)	\(\cos\theta\)	\(\tan\theta\)
(1,0)	\(0^\circ\)	0	1	0
(0,1)	\(90^\circ\)	1	0	undefined
(−1,0)	\(180^\circ\)	0	−1	0
(0,−1)	\(270^\circ\)	−1	0	undefined
(1,0)	\(360^\circ\)	0	1	0

Exercise 2

1. \begin{aligned}[t] \sin 330^\circ &= -\sin 30^\circ = -\dfrac{1}{2}\\ \cos 330^\circ &= \cos 30^\circ = \dfrac{\sqrt{3}}{2}\\ \tan 330^\circ &= -\tan 30^\circ = -\dfrac{1}{\sqrt{3}} \end{aligned}
2. If \(\theta\) is in the fourth quadrant, the related angle is \(360^\circ-\theta\).

Exercise 3

1. \(\sin 210^\circ = -\dfrac{1}{2}\)
2. \(\cos 315^\circ = \dfrac{1}{\sqrt{2}}\)
3. \(\tan 150^\circ = -\dfrac{1}{\sqrt{3}}\)

Exercise 4

1. In \(\triangle BCP\), we have \(h = a\,\sin B\). In \(\triangle ACP\), we have \(h = b\,\sin A\).
2. Hence \(a\,\sin B = b\,\sin A \ \implies \ \dfrac{a}{\sin A} = \dfrac{b}{\sin B}\).
3. In \(\triangle BCM\), we have \(h = a\,\sin B\). In \(\triangle ACM\), we have \(h = b\,\sin(180^\circ - A) = b\,\sin A\).
4. Again it follows that \(\dfrac{a}{\sin A} = \dfrac{b}{\sin B}\).

Exercise 5

Using \(A = \dfrac{1}{2} ab\,\sin \theta\), we have

\begin{align*} 5 = \dfrac{1}{2}\times 5\times 4 \times \sin \theta \ &\implies \ \sin \theta = \dfrac{1}{2}\\ \ &\implies \ \theta = 30^\circ, 150^\circ. \end{align*}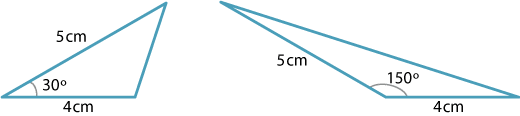

Detailed description of diagram

Exercise 6

\(\dfrac{1}{2}ac\,\sin B = \dfrac{1}{2}bc\,\sin A \ \implies \ a\,\sin B = b\,\sin A \ \implies \ \dfrac{a}{\sin A} = \dfrac{b}{\sin B}\)

Exercise 7

\(\text{LHS} = \dfrac{1}{\sec\theta + \tan \theta} = \dfrac{1}{\dfrac{1}{\cos\theta} + \dfrac{\sin\theta}{\cos\theta}} = \dfrac{\cos\theta}{1+\sin\theta} = \text{RHS}\)

Exercise 8

The double angle formula for cosine gives \(\cos 30^\circ = 1 - 2\sin^2 15^\circ\). So

\begin{align*} \sin^2 15^\circ &= \dfrac{1}{2}\bigl(1 - \cos 30^\circ\bigr)\\ &= \dfrac{1}{2}\Bigl(1 - \dfrac{\sqrt 3}{2}\Bigr)\\ &= \dfrac{1}{4}\bigl(2 - \sqrt 3\bigr). \end{align*}

Hence \(\sin 15^\circ = \dfrac{1}{2}\sqrt{2 - \sqrt{3}}\). (Take the positive square root, as \(\sin15^\circ\) is positive.)

An alternative method is to start from \(\sin 30^\circ = 2\sin 15^\circ\cos 15^\circ\). Proceed by squaring both sides of the equation and using the Pythagorean identity.

Exercise 9

Using the double angle formulas, we have

\[ \tan 2\theta = \dfrac{\sin2\theta}{\cos 2\theta} = \dfrac{2\sin\theta\,\cos\theta}{\cos^2\theta - \sin^2\theta}. \]

If we assume that \(\tan \theta\) is defined, then we can divide the numerator and denominator by \(\cos^2\theta\) to obtain

\[ \tan 2\theta = \dfrac{2\,\dfrac{\sin\theta}{\cos\theta}}{1-\dfrac{\sin^2\theta}{\cos^2\theta}} = \dfrac{2\tan\theta}{1-\tan^2\theta}. \]

Note that \(\tan 2\theta\) is defined if and only if \(\cos 2\theta = \cos^2\theta - \sin^2\theta \ne 0\), in which case \(\tan \theta\) cannot equal \(\pm 1\).

Exercise 10

\begin{align*} \sin(A+B) &= \cos\bigl(90^\circ -(A+B)\bigr)\\ &= \cos\bigl( (90^\circ -A)-B\bigr)\\ &= \cos(90^\circ -A)\,\cos B + \sin(90^\circ - A)\,\sin B\\ &= \sin A\,\cos B + \cos A\,\sin B. \end{align*}

Replacing \(B\) with \(-B\) gives the remaining formula.

Exercise 11

1. These follow easily by considering the triangles \(BCD\) and \(ACD\).
2. Area of \(\triangle ABC\) \(=\) area of \(\triangle BCD\) \(+\) area of \(\triangle ACD\).
3. So \(\dfrac{1}{2} ab\,\sin(\alpha + \beta) = \dfrac{1}{2} ay\,\sin \alpha + \dfrac{1}{2} by\,\sin \beta\).
4. Substitute \(y = b\cos\beta\) into the first term on the right-hand side of the equation from part (b) and \(y=a\cos\alpha\) into the second term. Then divide both sides by \(\dfrac{1}{2}ab\) to obtain the sine expansion.

Exercise 12

\(\tan 15^\circ = \tan(45^\circ - 30^\circ) = \dfrac{1-\frac{1}{\sqrt{3}}}{1+\frac{1}{\sqrt{3}}} = \dfrac{\sqrt{3}-1}{\sqrt{3}+1}\) (By multiplying both the numerator and the denominator by \(\sqrt{3} - 1\), this answer can be simplified to \(\tan 15^\circ = 2 - \sqrt{3}\).)

Exercise 13

Put \(\theta = 67\frac{1}{2}^\circ\) into the double angle formula:

\begin{align*} \tan 135^\circ = \dfrac{2t}{1-t^2} \ &\implies \ -1 = \dfrac{2t}{1-t^2}\\ \ &\implies \ t^2 - 2t - 1 = 0\\ \ &\implies \ t = 1 \pm \sqrt{2}. \end{align*}

Hence, \(\tan 67\frac{1}{2}^\circ =1+\sqrt{2}\).

(Here we take the positive square root, since \(\tan 67\frac{1}{2}^\circ\) is positive.)

Exercise 14

With \(m_2=2\) and \(\gamma = 45^\circ\), we have

\[ 1 = \Biggl|\dfrac{m-2}{1+2m}\Biggr|. \]

Hence \(m-2 = 2m+1\) or \(m-2 = -(2m+1)\), giving \(m = -3\) and \(m=\dfrac{1}{3}\).

The two lines obtained are perpendicular.

Exercise 15

Since the angles subtended at the centre of the hexagon are each \(60^\circ\), we can divide the inner and outer hexagons into equilateral triangles. The side length of the inner triangles is \(r\). After applying Pythagoras' theorem, we find that the side length of each triangle in the outer hexagon is \(\dfrac{2}{\sqrt{3}} r\). Hence, comparing perimeters,

\[ 6r \leq 2\pi r \leq 6 \times \dfrac{2}{\sqrt{3}}r. \]

Dividing by \(2r\) and simplifying gives the desired result.

Exercise 16

Exercise 17

Exercise 18

\begin{align*} \sin 3\theta &= \sin(2\theta +\theta)\\ &= \sin 2\theta\,\cos \theta + \cos 2\theta\,\sin \theta\\ &= 2\sin\theta\,\cos^2\theta + \bigl(\cos^2\theta-\sin^2\theta\bigr)\,\sin\theta\\ &= 2\sin\theta\,\bigl(1-\sin^2\theta\bigr)+\bigl(1-2\sin^2\theta\bigr)\,\sin\theta\\ &= 3\sin\theta - 4\sin^3\theta \end{align*}

Exercise 19

There are a number of ways to do this problem. We could begin by factoring out 5, but we will do it as follows:

\[ A\sin(x + \alpha) = A\bigl(\sin x\,\cos \alpha + \cos x\,\sin \alpha\bigr) = 3\cos x - 4\sin x. \]

Since this is an identity in \(x\), we can equate coefficients and write

\[ A\sin \alpha = 3 \qquad \text{and} \qquad A\cos \alpha = -4. \]

Squaring and adding these equations gives \(A=5\), and hence \(\sin \alpha = \dfrac{3}{5}\) and \(\cos \alpha = -\dfrac{4}{5}\). So we can take \(\alpha\) as an angle in the second quadrant and the calculator gives \(\alpha \approx 143.1^\circ\). Hence \(3\cos x - 4\sin x = 5\sin(x+\alpha)\), with \(\alpha \approx 143.1^\circ\).

Exercise 20

The double angle formula for cosine gives \(\cos \theta = \cos^2 {\dfrac{\theta}{2}} - \sin^2 {\dfrac{\theta}{2}}\). So, using the triangle arising from \(t= \tan {\dfrac{\theta}{2}}\), we have

\[ \cos \theta = \dfrac{1}{1+t^2} - \dfrac{t^2}{1+t^2} = \dfrac{1-t^2}{1+t^2}. \]

Exercise 21

Let \(\alpha = \dfrac\theta2\) and \(t = \tan \alpha\). Then

\[ \dfrac{2t}{1 + t^2} = \dfrac{\dfrac{2\sin\alpha}{\cos\alpha}}{1 + \dfrac{\sin^2\alpha}{\cos^2\alpha}} = \dfrac{2\sin\alpha\,\cos\alpha}{\cos^2\alpha + \sin^2\alpha} = 2\sin\alpha\,\cos\alpha = \sin2\alpha = \sin\theta, \] using the Pythagorean identity and the double angle formula for sine.