Links forward
The \(t\) formulas
Introducing the parameter \(t = \tan\dfrac{\theta}{2}\) turns out to be a very useful tool in solving certain types of trigonometric equations and also in finding certain integrals involving trigonometric functions. The basic idea is to relate \(\sin\theta\), \(\cos\theta\) and even \(\tan\theta\) to the tangent of half the angle. This can be done using the double angle formulas.
We let \(t= \tan\dfrac{\theta}{2}\) and so we can draw the following triangle with sides 1, \(t\), \(\sqrt{1+t^2}\).
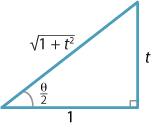
Detailed description of diagram
Now \(\sin 2\alpha = 2\sin\alpha\cos\alpha\), so replacing \(2\alpha\) with \(\theta\) we have
\[ \sin \theta = 2 \sin\dfrac{\theta}{2}\, \cos\dfrac{\theta}{2}. \]From the triangle, we have
\[ \sin \theta = 2 \times \dfrac{t}{\sqrt{1+t^2}} \times \dfrac{1}{\sqrt{1+t^2}} = \dfrac{2t}{1+t^2}. \]This is referred to as the \(t\) formula for \(\sin \theta\).
Exercise 20
Use the geometric method above to derive the \(t\) formula
\[ \cos \theta = \dfrac{1-t^2}{1+t^2} \] and deduce that \(\tan\theta = \dfrac{2t}{1-t^2}\), for \(t \ne \pm 1\).Exercise 21
The geometric proof of the \(t\) formula for \(\sin\theta\) given above assumes that the angle \(\dfrac{\theta}{2}\) is acute. Give a general algebraic proof of the formula.
One application of the \(t\) formulas is to solving certain types of trigonometric equations.
Example
Solve \(\cos\theta + \sin\theta = \dfrac{1}{2}\), for \(0^\circ \leq \theta \leq 360^\circ\), correct to one decimal place.
Solution
Put \(t = \tan\dfrac{\theta}{2}\). Then
\[ \dfrac{1-t^2}{1+t^2} + \dfrac{2t}{1+t^2} = \dfrac{1}{2}. \]This rearranges to \(3t^2-4t-1=0\), whose solutions are \(t = \dfrac{2\pm\sqrt{7}}{3} \approx 1.549, -0.215\). Taking the inverse tangents (in degrees) and doubling, we obtain the solutions \(\theta \approx 114.3^\circ, 335.7^\circ\) in the given range.
  |
This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations |
Contributors Term of use |