Content

Trigonometric identities

The Pythagorean identity

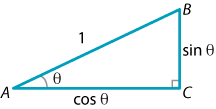
There are many important relationships between the trigonometric functions which are of great use, especially in calculus. The most fundamental of these is the Pythagorean identity. For acute angles, this is easily proven from the following triangle \(ABC\) with hypotenuse of unit length.

Right –angled triangle ABC.
Detailed description of diagram

With \(\angle BAC = \theta\), we see that \(AC = \cos\theta\) and \(BC = \sin\theta\). Hence Pythagoras' theorem tells us that

\[ \cos^2\theta + \sin^2\theta =1. \]

This formula holds for all angles, since every angle can be related to an angle in the first quadrant whose sines and cosines differ only by a sign, which is dealt with by squaring. Dividing this equation respectively by \(\cos^2\theta\) and by \(\sin^2\theta\), we obtain

\[ 1 + \tan^2\theta = \sec^2\theta \qquad \text{and} \qquad \cot^2\theta + 1= \operatorname{cosec}^2\theta. \]

From these standard identities, we can prove a variety of results.

Example

Prove the following identities:

\((1-\sin\theta)(1+\sin\theta) = \cos^2\theta\)
\(\dfrac{2\cos^3\theta-\cos\theta}{\sin\theta\,\cos^2\theta - \sin^3\theta} = \cot\theta\).

Solution

\begin{aligned}[t] \text{LHS} &= (1-\sin\theta)(1+\sin\theta)\\ &= 1-\sin^2\theta & &\text{(difference of two squares)}\\ &= \cos^2\theta & &\text{(Pythagorean identity)}\\ &= \text{RHS} \end{aligned}
\begin{aligned}[t] \text{LHS} &= \dfrac{2\cos^3\theta-\cos\theta}{\sin\theta\,\cos^2\theta - \sin^3\theta}\\ &= \dfrac{\cos\theta\,\bigl(2\cos^2\theta -1\bigr)}{\sin\theta\,\bigl(\cos^2\theta - \sin^2\theta\bigr)}\\ &=\dfrac{\cos\theta\,\bigl(2\cos^2\theta -1\bigr)}{\sin\theta\,\bigl(\cos^2\theta -(1-\cos^2\theta)\bigr)}\\ &=\dfrac{\cos\theta\,\bigl(2\cos^2\theta -1\bigr)}{\sin\theta\,\bigl(2\cos^2\theta - 1\bigr)}\\ &= \dfrac{\cos\theta}{\sin\theta}\\ &= \cot\theta\\ &= \text{RHS} \end{aligned}

Exercise 7

Prove that

\[ \dfrac{1}{\sec\theta + \tan\theta} = \dfrac{\cos\theta}{1+\sin\theta}. \]

Screencast of exercise 7

Double angle formulas

The sine and cosine functions are not linear. For example, \(\cos(A+B) \ne \cos A + \cos B\). The correct formula for \(\cos(A+B)\) is given in the next subsection. In the special case when \(A=B=\theta\), we would like to obtain a simple formula for \(\cos(2\theta) = \cos 2\theta\), called the double angle formula. It is particularly useful in applications and in calculus and is quite easy to derive.

Consider the following isosceles triangle \(ABC\), with sides \(AB\) and \(AC\) both of length 1 and apex angle \(2\theta\). We will need to assume, for the present, that \(0^\circ < \theta < 90^\circ\).

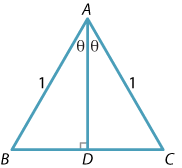
Triangle ABC, isosceles triangle with AB = AC = 1. D is the midpoint of BC with AD perpendicular to BC. Angle BAD = angle CAD = theta.

Let \(AD\) be the perpendicular bisector of the interval \(BC\). Then, using basic properties of an isosceles triangle, we know that \(AD\) bisects \(\angle BAC\) and so \(BD = DC = \sin\theta\). Applying the cosine rule to the triangle \(ABC\), we immediately have

\begin{align*} \cos2\theta &= \dfrac{1^2 + 1^2 - 4 \sin^2\theta}{2\times 1\times 1}\\ &= \dfrac{2 - 4\sin^2\theta}{2}\\ &= 1 - 2\sin^2\theta. \end{align*}

Replacing 1 by \(\cos^2\theta + \sin^2\theta\), we arrive at the double angle formula

\[ \cos 2\theta = \cos^2\theta - \sin^2\theta. \]

This may also be written as \( \cos 2\theta = 2\cos^2\theta -1\) or \(\cos 2\theta = 1-2\sin^2\theta\), but is best learnt in the form given above.

We derived this formula under the assumption that \(\theta\) was between \(0^\circ\) and \(90^\circ\), but the formula in fact holds for all values of \(\theta\). We shall see this in the next subsection, where we prove the general expansion formula for \(\cos(A + B)\).

Example

Find \(\cos 22\frac{1}{2}^\circ\) in surd form.

Solution

Putting \(\theta = 22\frac{1}{2}^\circ\) into the double angle formula \(\cos 2\theta = 2\cos^2\theta -1\) and writing \(x\) for \(\cos 22\frac{1}{2}^\circ\), we obtain

\begin{align*} \cos 45^\circ &= 2x^2-1\\ \dfrac{1}{\sqrt{2}} &= 2x^2-1 \\ 2x^2& =\dfrac{1+\sqrt{2}}{\sqrt{2}}\\ x &= \sqrt{\dfrac{1+\sqrt{2}}{2\sqrt{2}}}, \end{align*} which simplifies to \(\dfrac{1}{2}\sqrt{2 + \sqrt{2}}\).

We can also find a double angle formula for sine using the same diagram.

Triangle ABC, isosceles triangle with AB = AC = 1. D is the midpoint of BC with AD perpendicular to BC. Angle BAD = angle CAD = theta.

In this case, we write down formulas for the area of \(\triangle ABC\) in two ways:

On the one hand, the area is given by \(\dfrac{1}{2} AB \cdot AC \, \sin (\angle BAC) = \dfrac{1}{2}\sin 2\theta\).
Since \(AD=\cos\theta\), we can alternatively split the triangle into two right-angled triangles and write the area as \(2\times \dfrac{1}{2} \sin\theta\, \cos\theta = \sin\theta\, \cos\theta\).

Equating these two expressions for the area, we obtain

\[ \sin 2\theta = 2\sin\theta\cos\theta. \]

As before, we assumed that \(\theta\) lies between \(0^\circ\) and \(90^\circ\), but the formula is valid for all values of \(\theta\).

Exercise 8

Find \(\sin 15^\circ\) in surd form.

From the Pythagorean identity and the double angle formula for cosine, we have

\begin{align*} \cos^2\theta + \sin^2\theta &= 1 \\ \cos^2\theta - \sin^2\theta &= \cos 2\theta. \end{align*}

Adding these equations and dividing by 2 we obtain \(\cos^2\theta = \dfrac{1}{2}(\cos 2\theta + 1)\), while subtracting them and dividing by 2 we obtain \(\sin^2\theta = \dfrac{1}{2}(1-\cos 2\theta)\). These formulas are very important in integral calculus, as discussed in the module The calculus of trigonometric functions.

Exercise 9

Use the double angle formulas for sine and cosine to show that

\[ \tan 2\theta = \dfrac{2\tan \theta}{1-\tan^2\theta}, \qquad \text{for } \tan\theta \ne \pm 1. \]

Summary of double angle formulas
\(\sin 2\theta = 2\sin\theta\cos\theta\)
\begin{aligned}[t]\cos 2\theta &= \cos^2\theta-\sin^2\theta\\ &= 2\cos^2\theta-1\\ &= 1-2\sin^2\theta\end{aligned}
\(\tan 2\theta = \dfrac{2\tan \theta}{1-\tan^2\theta}\),	for tan\(\theta \ne \pm 1\)

Trigonometric functions of compound angles

In the previous subsection, we derived formulas for the trigonometric functions of double angles. That derivation, which used triangles, was only valid for a limited range of angles, although the formulas remain true for all angles.

In this subsection we find the expansion formulas for \(\sin({A+B})\), \(\sin({A-B})\), \(\cos({A+B})\) and \(\cos({A-B})\), which are valid for all \(A\) and \(B\). The double angle formulas can be recovered by putting \(A=B=\theta\).

These formulas are quite central in trigonometry. In the module The calculus of trigonometric functions, they are used to find, among other things, the derivative of the sine function.

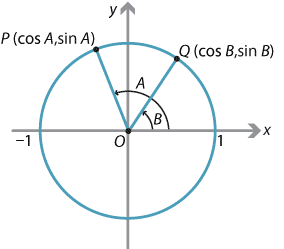
To prove the \(\cos(A-B)\) formula, from which we can obtain the other expansions, we return to the circle definition of the trigonometric functions.

Consider two points \(P(\cos A, \sin A)\) and \(Q(\cos B, \sin B)\) on the unit circle, making angles \(A\) and \(B\) respectively with the positive \(x\)-axis.

Circle with radius of 1, centre the origin O.
Detailed description of diagram

We will calculate the distance \(PQ\) in two ways and then equate the results. First we apply the cosine rule to the triangle \(OPQ\). Note that, in the diagram above, \(\angle POQ = A-B\). In general, it is always the case that \(\cos(\angle POQ) = \cos(A-B)\). So the cosine rule gives

\[ PQ^2 = 1^2+1^2 -2\times 1\times 1\times \cos(A-B) = 2-2\cos(A-B). \]

On the other hand, using the square of the distance formula from coordinate geometry,

\begin{align*} PQ^2 &= (\cos B - \cos A)^2 + (\sin B - \sin A)^2\\ &= \cos^2 A + \sin^2 A + \cos^2 B + \sin ^2 B - 2\cos A\,\cos B - 2\sin A\,\sin B\\ &= 2-2(\cos A\,\cos B + \sin A\,\sin B). \end{align*}

Equating the two expressions for \(PQ^2\), we have

\[ \cos(A-B) = \cos A\,\cos B + \sin A\,\sin B. \]

We can easily obtain the formula for \(\cos(A+B)\) by replacing \(B\) with \(-B\) in the formula for \(\cos(A-B)\) and recalling that \(\cos(-\theta) = \cos\theta\) (the cosine function is an even function) and \(\sin(-\theta) = -\sin\theta\) (the sine function is an odd function).

Hence

\begin{align*} \cos(A+B) &= \cos A\,\cos(-B) + \sin A\,\sin(-B)\\ &= \cos A\,\cos B - \sin A\,\sin B. \end{align*}

Using the identity \(\sin\theta = \cos(90^\circ - \theta)\), we can show that

\begin{align*} \sin(A+B) &= \sin A\,\cos B + \cos A\,\sin B,\\ \sin(A-B) &= \sin A\,\cos B - \cos A\,\sin B. \end{align*}

These four compound angle formulas are important and the student should remember them. Most other trigonometric identities can be derived from these and the standard Pythagorean identity \(\cos^2\theta + \sin^2\theta = 1\).

Exercise 10

Use the identity \(\sin\theta = \cos(90^\circ - \theta)\) to derive the sine expansions.

The following exercise gives a simple geometric derivation of the sine expansion.

Exercise 11

Fix acute angles \(\alpha\) and \(\beta\). Construct a triangle \(ABC\) as shown in the following diagram. (Start by drawing the line interval \(CD\). Then construct the right-angled triangles \(BCD\) and \(ACD\).)

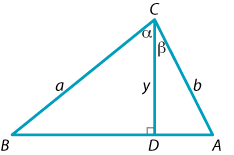
Triangle ABC, AC = b, BC = a. D is a point on AB such that CD is perpendicular to AB. CD = y. Angle BCD = alpha and angle ACD = beta.

Prove that \(y = a \cos \alpha\) and \(y = b \cos\beta\).
By comparing areas, show that \[ \dfrac{1}{2}ab\,\sin (\alpha +\beta) = \dfrac{1}{2}ay\,\sin \alpha + \dfrac{1}{2}by\,\sin \beta. \]
Deduce the expansion formula for \(\sin(\alpha+\beta)\).

Using the compound angle formulas, we can extend the range of angles for which we can obtain exact values for the trigonometric functions.

Example

Find the exact value of

\(\cos 75^\circ\)
\(\sin 75^\circ\)
\(\cos 105^\circ\).

solution

\begin{aligned}[t] \cos 75^\circ &= \cos(45^\circ + 30^\circ)\\ &= \cos 45^\circ\cos 30^\circ - \sin 45^\circ\sin 30^\circ\\ &= \dfrac{1}{\sqrt{2}}\dfrac{\sqrt{3}}{2} - \dfrac{1}{\sqrt{2}}\dfrac{1}{2}\\ &= \dfrac{1}{4}\bigl(\sqrt{6}-\sqrt{2}\bigr) \end{aligned}
\begin{aligned}[t] \sin 75^\circ & = \sin(45^\circ+ 30^\circ)\\ &= \sin 45^\circ\cos 30^\circ + \cos 45^\circ\sin 30^\circ\\ &= \dfrac{1}{\sqrt{2}}\dfrac{\sqrt{3}}{2} + \dfrac{1}{\sqrt{2}}\dfrac{1}{2}\\ &= \dfrac{1}{4}\bigl(\sqrt{6}+\sqrt{2}\bigr) \end{aligned}
\begin{aligned}[t] \cos 105^\circ &= \cos(45^\circ+ 60^\circ)\\ &= \cos 45^\circ\cos 60^\circ - \sin 45^\circ\sin 60^\circ\\ &= \dfrac{1}{\sqrt{2}}\dfrac{1}{2} - \dfrac{1}{\sqrt{2}}\dfrac{\sqrt{3}}{2}\\ &= \dfrac{1}{4}\bigl(\sqrt{2} - \sqrt{6}\bigr) \end{aligned}

(Note that we could obtain \(\cos 105^\circ\) directly from \(\cos 75^\circ\), since the two angles are supplementary.)

We can also find expansions for \(\tan(A+B)\) and \(\tan(A-B)\). Recalling that \(\tan\theta = \dfrac{\sin \theta}{\cos\theta}\), we can write

\[ \tan(A+B) = \dfrac{\sin(A+B)}{\cos(A+B)} = \dfrac{\sin A\,\cos B + \cos A\,\sin B}{\cos A\,\cos B - \sin A\,\sin B}. \]

Dividing the numerator and denominator by \(\cos A\,\cos B\), we obtain

\[ \tan(A+B) = \dfrac{\dfrac{\sin A}{\cos A} + \dfrac{\sin B}{\cos B}}{1 - \dfrac{\sin A\,\sin B}{\cos A\,\cos B}} = \dfrac{\tan A+\tan B}{1-\tan A\,\tan B}. \]

Since \(\tan(-B) = -\tan B\), we have

\[ \tan(A-B) = \dfrac{\tan A-\tan B}{1+\tan A\,\tan B}. \]

Note carefully the pattern with the signs.

Exercise 12

Find the exact value of \(\tan 15^\circ\).

Putting \(A=B=\theta\) in the expansion formula for \(\tan(A+B)\), we obtain

\[ \tan 2\theta = \dfrac{2\tan\theta}{1-\tan^2\theta}. \]

Exercise 13

Show that \(t = \tan 67\frac{1}{2}^\circ\) satisfies the quadratic equation \(t^2-2t-1=0\) and hence find its exact value.

Screencast of exercise 13

The angle between two lines

The tangent expansion formula can be used to find the angle, or rather the tangent of the angle, between two lines.

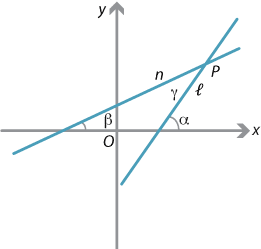
Line marked n, intercepting negative x axis and positive y axis angle created by line and x axis marked as beta.
Detailed description of diagram

Suppose two lines \(\ell\) and \(n\) with gradients \(m_1\) and \(m_2\), respectively, meet at the point \(P\). The gradient of a line is the tangent of the angle it makes with the positive \(x\)-axis. So, if \(\ell\) and \(n\) make angles \(\alpha\) and \(\beta\), respectively, with the positive \(x\)-axis, then \(\tan\alpha = m_1\) and \(\tan\beta = m_2\). We will assume for the moment that \(\alpha > \beta\), as in the diagram above.

Now, if \(\gamma\) is the angle between the lines (as shown), then \(\gamma = \alpha - \beta\). Hence

\[ \tan \gamma = \tan(\alpha-\beta) = \dfrac{\tan\alpha - \tan \beta}{1+\tan\alpha\,\tan\beta} = \dfrac{m_1-m_2}{1+m_1m_2}, \] provided \(m_1m_2 \ne -1\). If \(m_1m_2 = -1\), the two lines are perpendicular and \(\tan\gamma\) is not defined.

In general, the above formula may give us a negative number, since it may be the tangent of the obtuse angle between the two lines.

Hence, if we are interested only in the acute angle, since \(\tan (180^\circ - \theta)= -\tan \theta\), we can take the absolute value and say that, if \(\gamma\) is the acute angle between the two lines, then

\[ \tan\gamma = \Biggl|\dfrac{m_1-m_2}{1+m_1m_2}\Biggr|, \]

provided the lines are not perpendicular.

Example

Find, to the nearest degree, the acute angle between the lines \(y= 2x-1\) and \(y=3x+4\).

Solution

Here \(m_1=2\) and \(m_2=3\). So, if \(\theta \) is the acute angle between the two lines, we have

\[ \tan \theta = \Biggl|\dfrac{2-3}{1+6}\Biggr| = \dfrac{1}{7} \] and therefore \(\theta \approx 8^\circ\).

Exercise 14

Find the two values of \(m\) such that the angle between the lines \(y=mx\) and \(y=2x\) is \(45^\circ\). What is the relationship between the two lines you obtain?

If we define the angle between two curves at a point of intersection to be the angle between their tangents at that point, then the above formula — along with some differential calculus — can be used to find that angle.

Next page - Content - Radian measure