Content
The trigonometric ratios
If we fix an acute angle \(\theta\), then all right-angled triangles that have \(\theta\) as one of their angles are similar. So, in all such triangles, corresponding pairs of sides are in the same ratio.
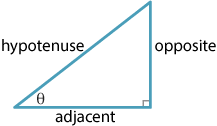
The side opposite the right angle is called the hypotenuse. We label the side opposite \(\theta\) as the opposite and the remaining side as the adjacent. Using these names we can list the following standard ratios:
\begin{align*} \sin \theta &= \dfrac{\text{opposite}}{\text{hypotenuse}}, & \cos \theta &= \dfrac{\text{adjacent}}{\text{hypotenuse}}, & \tan \theta &= \dfrac{\text{opposite}}{\text{adjacent}}. \end{align*}Allied to these are the three reciprocal ratios, cosecant, secant and cotangent:
\begin{align*} \operatorname{cosec} \theta &= \dfrac{\text{hypotenuse}}{\text{opposite}}, & \sec \theta &= \dfrac{\text{hypotenuse}}{\text{adjacent}}, & \cot \theta &= \dfrac{\text{adjacent}}{\text{opposite}}. \end{align*}These are called the reciprocal ratios as
\begin{align*} \operatorname{cosec} \theta &= \dfrac{1}{\sin\theta}, & \sec \theta &= \dfrac{1}{\cos\theta}, & \cot \theta &= \dfrac{1}{\tan\theta}. \end{align*}The trigonometric ratios can be used to find lengths and angles in right-angled triangles.
Example
Find the value of \(x\) in the following triangle.
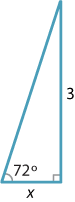
Solution
We have
\[ \dfrac{x}{3} = \cot 72^\circ = \dfrac{1}{\tan 72^\circ}. \]Hence
\[ x = \dfrac{3}{\tan 72^\circ} \approx 0.97, \quad \text{correct to two decimal places}. \]Special angles
The trigonometric ratios of the angles \(30^\circ\), \(45^\circ\) and \(60^\circ\) can be easily expressed as fractions or surds, and students should commit these to memory.
| \(\theta\) | \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
|---|---|---|---|
| \(30^\circ\) | \(\dfrac{1}{2}\) | \(\dfrac{\sqrt 3}{2}\) | \(\dfrac{1}{\sqrt 3}\) |
| \(45^\circ\) | \(\dfrac{1}{\sqrt 2}\) | \(\dfrac{1}{\sqrt 2}\) | 1 |
| \(60^\circ\) | \(\dfrac{\sqrt 3}{2}\) | \(\dfrac{1}{2}\) | \(\sqrt 3\) |
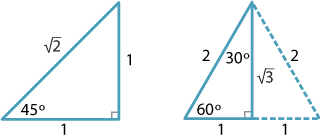
Triangles for the trigonometric ratios of special angles.
Detailed description of diagram
Extending the angles
In the module Further trigonometry (Year 10), we showed how to redefine the trigonometric functions in terms of the coordinates of points on the unit circle. This allows the definition of the trigonometric functions to be extended to the second quadrant.
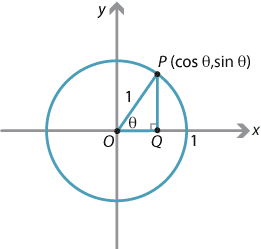
Detailed description of diagram
If the angle \(\theta\) belongs to the first quadrant, then the coordinates of the point \(P\) on the unit circle shown in the diagram are simply \((\cos \theta, \sin \theta)\).
Thus, if \(\theta\) is the angle between \(OP\) and the positive \(x\)-axis:
- the cosine of \(\theta\) is defined to be the \(x\)-coordinate of the point \(P\) on the unit circle
- the sine of \(\theta\) is defined to be the \(y\)-coordinate of the point \(P\) on the unit circle.
We can apply this definition to any angle.
The tangent ratio is then defined by
\[ \tan\theta = \dfrac{\sin\theta}{\cos\theta}, \] provided \(\cos\theta\) is not zero.As an example, let us take \(\theta\) to be \(30^\circ\), so \(P\) has coordinates \((\cos 30^\circ, \sin 30^\circ)\). Now move the point \(P\) around the circle to \(P'\), so that \(OP'\) makes an angle of \(150^\circ\) with the positive \(x\)-axis. Note that \(30^\circ\) and \(150^\circ\) are supplementary angles. The coordinates of \(P'\) are \((\cos 150^\circ, \sin 150^\circ)\).
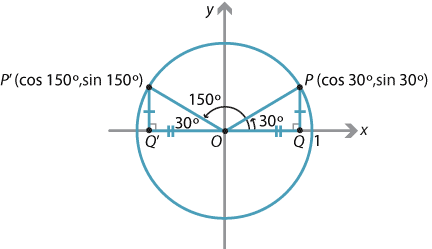
Detailed description of diagram
But we can see that the triangles \(OPQ\) and \(OP'Q'\) are congruent, so the \(y\)-coordinates of \(P\) and \(P'\) are the same. Thus, \(\sin 150^\circ = \sin 30^\circ\). Also, the \(x\)-coordinates of \(P\) and \(P'\) have the same magnitude but opposite sign, so \(\cos 150^\circ = -\cos 30^\circ\).
From this typical example, we see that if \(\theta\) is any obtuse angle, then its supplement \({180^\circ - \theta}\) is acute, and the sine of \(\theta\) is given by
\[ \sin \theta = \sin (180^\circ - \theta), \qquad \text{where } 90^\circ < \theta < 180^\circ. \]Similarly, if \(\theta\) is any obtuse angle, then the cosine of \(\theta\) is given by
\[ \cos \theta = -\cos (180^\circ - \theta), \qquad \text{where } 90^\circ < \theta < 180^\circ. \]In words this says:
- the sine of an obtuse angle equals the sine of its supplement
- the cosine of an obtuse angle equals minus the cosine of its supplement.
Exercise 1
On the unit circle, place the point \(P\) corresponding to each of the angles \(0^\circ\), \(90^\circ\), \(180^\circ\), \(270^\circ\) and \(360^\circ\). By considering the coordinates of each of these points, complete the following table of trigonometric ratios.
| Coordinates of \(P\) | \(\theta\) | \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
|---|---|---|---|---|
| \(0^\circ\) | ||||
| \(90^\circ\) | undefined | |||
| \(180^\circ\) | ||||
| \(270^\circ\) | undefined | |||
| \(360^\circ\) |
