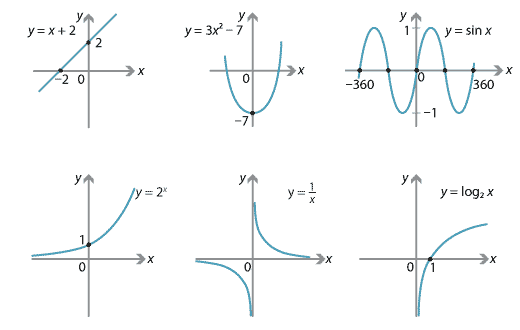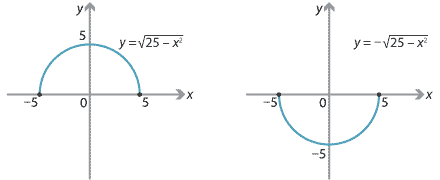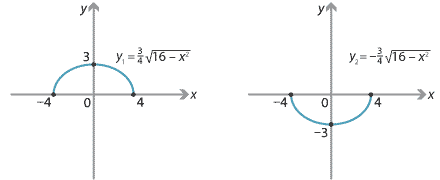Content

The concept of a function

When a quantity \(y\) is uniquely determined by some other quantity \(x\) as a result of some rule or formula, then we say that \(y\) is a function of \(x\). (In other words, for each value of \(x\), there is at most one corresponding value of \(y\).)

We begin with six examples in which both \(x\) and \(y\) are real numbers:

• \(y=x+2\)
• \(y=3x^2-7\)
• \(y=\sin x\)

• \(y=2^x\)
• \(y=\dfrac{1}{x}\)
• \(y=\log_{2}x\).

We draw their graphs in the usual way, with the \(x\)-axis horizontal and the \(y\)-axis vertical.

six graphs
Detailed description

The first four functions are similar in that their formulas 'work' for all real numbers \(x\). For \(y=\dfrac{1}{x}\), we clearly need \(x\neq 0\), and for \(y=\log_{2}x\), we need \(x>0\). We will discuss this further in the section Domains and ranges.

What is a relation?

There are many naturally occurring formulas whose graphs are not the graphs of functions. For example:

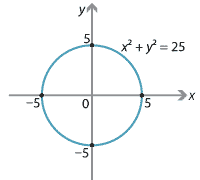
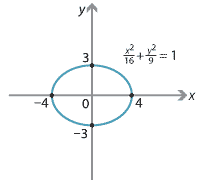
Circle, centre the origin of radius 5, with equation x squared plus y squared = 25 Ellipse with centre the origin with equation x squared over 16 + y squared over 9 = 1.
Two straight lines passing through the origin with equation y squared = x squared. Hyperbola with equation x squared over 16 – y squared over 9 = 1.

The first graph is a circle, the second is an ellipse, the third is two straight lines, and the fourth is a hyperbola. In each example, there are values of \(x\) for which there are two values of \(y\). So these are not graphs of functions.

It turns out that the most useful concept to help describe and understand this issue is very general.

Definition

A relation on the real numbers is any subset of \(\mathbb{R}\times\mathbb{R}\). That is, a relation on the reals is a set of ordered pairs of real numbers.

Thus the four graphs above and the graphs of the six example functions are all relations on the real numbers. Indeed, the graph of any function is a relation. Formally speaking, a function is a relation such that, for each \(x\), there is at most one ordered pair \((x,y)\).

Example

The line \(y=x\) divides the number plane into three relations.

The relation \(R_1 = \{\, (x,y) \mid x=y \,\}\) is the line itself. Note that, for each \(x\), there is only one value of \(y\).
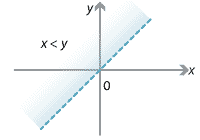
The relation \(R_2 = \{\, (x,y) \mid x<y \,\}\) consists of all points strictly above the line \(y=x\). Note that, for each \(x\), there are infinitely many values of \(y\).
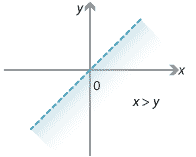
The relation \(R_3 = \{\, (x,y) \mid x>y \,\}\) consists of all points strictly below the line \(y=x\).

We can generalise the previous example to any line in the plane, as follows.

Example

The equation of a line \(l\) in the plane is given by \(ax+by+c=0\). This line determines, in a natural way, three relations on the reals: \begin{align*} R_1 &= \{\, (x,y) \mid ax+by+c=0 \,\} \\ R_2 &= \{\, (x,y) \mid ax+by+c<0 \,\} \\ R_3 &= \{\, (x,y) \mid ax+by+c>0 \,\}. \end{align*}

Example

Consider the circle \(x^2+y^2=r^2\), for some \(r>0\). There are three relations closely connected with this circle.

The circle itself: \[ R_1 = \{\, (x,y) \mid x^2+y^2=r^2 \,\}. \]
The interior of the circle: \[ R_2 = \{\, (x,y) \mid x^2+y^2<r^2 \,\}. \]
The exterior of the circle: \[ R_3 = \{\, (x,y) \mid x^2+y^2>r^2 \,\}. \]

Graphs and the vertical-line test

We have seen the graphs of several naturally described functions. A sensible question to ask, for a given graph in \(\mathbb{R}^2\), is whether it is the graph of a function.

The vertical-line test gives a simple geometric test for answering this question:

If we can draw a vertical line \(x=c\) that cuts the graph more than once, then the graph is not the graph of a function.

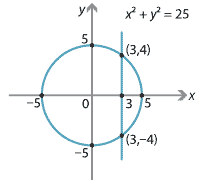
Returning to the graph of \(x^2+y^2=25\), we see that the vertical line \(x=3\) meets the graph at both \((3,4)\) and \((3,-4)\).

Circle, centre the origin of radius 5, with equation x squared plus y squared = 25.
Detailed description

Hence, the graph of \(x^2+y^2=25\) is not the graph of a function. The line \(x=6\) does not meet the graph at all, but this does not matter. In general:

for \(-5<c<5\), the line \(x=c\) meets the graph twice
for \(c=-5\) and for \(c=5\), the line \(x=c\) meets the graph once
for \(c<-5\) and for \(c>5\), the line \(x=c\) does not meet the graph.

Relations which determine functions

There is a natural way in which we can use the relation \(x^2+y^2=25\) to construct two functions. Solving \(x^2+y^2=25\) for \(y\) gives \[ y^2 = 25-x^2 \] \[ y = \sqrt{25-x^2} \quad\text{or}\quad y=-\sqrt{25-x^2}. \]

The graph of the first of these functions is the 'top half' of the circle, and the graph of the second is the 'bottom half' of the circle.

Two semi circle graphs
Detailed description

Example

Consider the ellipse \[ \dfrac{x^2}{16} + \dfrac{y^2}{9} = 1. \]

Find two functions whose graphs together include all points on the ellipse.

Solution

Solve for \(y\): \begin{align*} \dfrac{x^2}{16}+\dfrac{y^2}{9} &= 1 \\ \dfrac{y^2}{9} &= 1-\dfrac{x^2}{16} \\ y^2 &= \dfrac{9}{16}\bigl(16-x^2\bigr) \\ y &= \pm\dfrac{3}{4}\sqrt{16-x^2}. \end{align*} Hence, \[ y_1 = \dfrac{3}{4}\sqrt{16-x^2} \quad\text{and}\quad y_2 = -\dfrac{3}{4}\sqrt{16-x^2} \]

are two such functions.

Two graphs shown.
Detailed description

Note that the two graphs overlap in the points \((4,0)\) and \((-4,0)\). This is not an issue.

Next page - Content - Domains and ranges