Assumed knowledge

• The content of the module Quadratic equations (Years 9–10) .
• The content of the module Algebra review, which includes factoring quadratic expressions, completing the square and solving quadratic equations using various techniques including the quadratic formula.
• The content of the module Coordinate geometry.

Motivation

Quadratic equations arose in antiquity in the context of problem solving. These problems were generally expressed verbally, but their solution involved some method for solving a quadratic equation — often also expressed verbally.

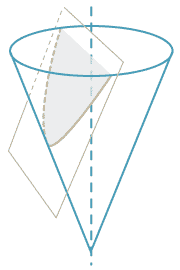
Detailed description of diagram

The Greeks studied the parabola and its geometry. This curve occurs naturally as the edge of the cross-section of a cone sliced at an angle to its main axis.

The parabola can also be thought of as the graph of the quadratic function. It models the path taken by a ball thrown under gravity at an angle to the horizontal, assuming we ignore air resistance.

Since the Greeks did not have the notion of a coordinate system, their studies were heavily geometric and often hard to understand. With the advent of coordinate geometry, the study of the parabola became much easier and a full and complete analysis became possible.

In this module, we will summarise all of the main features and properties of quadratic equations and functions.

We will also look at a geometric definition of the parabola and its representation using parametric equations.

One of the many interesting characteristics of the parabola is its reflective property, used in collecting light from a distant source.

It is not intended that all the material in this module be taught in one topic in the classroom. Our aim here is to present the teacher with a comprehensive overview of quadratic functions and the geometry of the parabola.

Next page - Content - The basic parabola