History and applications

An application to film and video

In modern film and video, one has the power to vary the width and height of the images being filmed and replayed. The ratio between the width and height of an image is called its aspect ratio. This ratio is commonly expressed in the form \(x:y\).

The most common aspect ratio used in movie theatres is \(2.35:1\), while the aspect ratio traditionally used for television and video is \(4:3 \approx 1.33:1\). It was found that the geometric mean of the numbers 2.35 and 1.33 provides a good compromise between the two different aspect ratios, distorting or cropping both in some sense equally. The geometric mean of 2.35 and 1.33 is approximately 1.77, and the ratio \(1.77:1\) corresponds approximately to \(16:9\). This is the aspect ratio adopted by the Society of Motion Picture and Television Engineers, and used for high-definition digital television.

Fibonacci numbers

The Fibonacci sequence

\[ 1,\ 1,\ 2,\ 3,\ 5,\ 8,\ 13,\ 21,\ 34,\ 55,\ 89,\ 144,\ \dots \]

was first discussed in Europe by Leonardo of Pisa (whose nickname was Fibonacci) in the early 13th century, although the sequence can be traced back to about 200 BCE in Indian literature. This sequence has produced a large amount of literature and has connections to many branches of mathematics.

In the Fibonacci sequence, each term is the sum of the two preceding terms. So if \(a_n\) is the \(n\)th term, we can write

\[ a_1 = a_2 = 1 \quad\text{and}\quad a_n = a_{n-1} + a_{n-2},\ \text{ for } n\geq 3. \]

This is an example of a second-order linear recurrence relation.

A first-order linear recurrence such as \(a_n = ka_{n-1}\), where \(k\) is a constant, is easily seen to have the solution \(a_n = a_1 \times k^{n-1}\), which is an exponential. By taking \(A = \dfrac{a_1}{k}\), we can write the solution as \(a_n = A\,k^n\).

One approach to solving a second-order linear recurrence is to guess an exponential solution of the form \(a_n = A\,k^n\), where \(A\) and \(k\) are non-zero constants. Substituting this into the recurrence for the Fibonacci sequence, we have

\[ A\,k^n = A\,k^{n-1} + A\,k^{n-2}. \]

Dividing by \(A\,k^{n-2}\), we see that \(k\) satisfies

\[ k^2 = k + 1, \]

which has solutions \(k = \dfrac{1}{2}(1 \pm \sqrt{5})\). Thus, we have found two exponential solutions

\[ a_n = A_1 \times \Biggl(\dfrac{1 + \sqrt{5}}{2}\Biggr)^n \qquad\text{and}\qquad a_n = A_2 \times \Biggl(\dfrac{1 - \sqrt{5}}{2}\Biggr)^n. \]

The theory of recurrence relations tells us that the general solution of this recurrence is obtained by summing these two solutions:

\[ a_n = A_1 \times \Biggl(\dfrac{1 + \sqrt{5}}{2}\Biggr)^n + A_2 \times \Biggl(\dfrac{1 - \sqrt{5}}{2}\Biggr)^n. \]

We can now use the initial condition \(a_1 = a_2 = 1\) to find that \(A_1 = \dfrac{1}{\sqrt{5}}\) and \(A_2 = -\dfrac{1}{\sqrt{5}}\). Finally, we have a formula for the \(n\)th Fibonacci number:

\[ a_n = \dfrac{1}{\sqrt{5}}\left(\Biggl(\dfrac{1+\sqrt{5}}{2}\Biggr)^n - \Biggl(\dfrac{1-\sqrt{5}}{2}\Biggr)^n\right). \]

Note that the number \(\dfrac{1}{2}(1 + \sqrt{5})\) that appears here is the golden ratio. One of many interesting facts about the Fibonacci sequence is that the only perfect squares in the sequence are 1 and 144.

The Greeks

The ancient Greek mathematicians were very interested in ratios. Indeed, much of their arithmetic was done geometrically using lengths and ratios. They found the link between ratios and music — hence the origin of the term harmonic mean.

The Greeks defined several different means. Less well known is the Heronian mean \(N(a,b)\) of two positive real numbers \(a\) and \(b\), which is the average of the three numbers \(a\), \(b\) and their geometric mean. That is,

\[ N(a,b) = \dfrac{a + b + \sqrt{ab}}{3}. \]

Notice that, for \(a,b>0\), we have

\[ \dfrac{a + b + \sqrt{ab}}{3} \geq \dfrac{2\sqrt{ab} + \sqrt{ab}}{3} = \sqrt{ab} \] and \[ \dfrac{a + b + \sqrt{ab}}{3} \leq \dfrac{a + b + \dfrac{a+b}{2}}{3} = \dfrac{a+b}{2}, \]

giving

\[ \sqrt{ab} \leq N(a,b) \leq \dfrac{a+b}{2}. \]

That is, the Heronian mean lies in between the geometric and arithmetic means.

Again, we can generalise and define the Heronian mean \(N\) of \(n\) positive real numbers \(a_1,a_2,\dots,a_n\) to be

\[ N = \dfrac{a_1 + a_2 + \dots + a_n + \sqrt[n]{a_1a_2\dots a_n}}{n+1}. \]

The Greeks were also interested in various types of sequences and series. They of course knew the sequence of square numbers

\[ 1,\ 4,\ 9,\ 16,\ \dots \]

but they also introduced the sequence of triangular numbers

\[ 1,\ 3,\ 6,\ 10,\ \dots \]

given by \(T_1 = 1\) and \(T_n = T_{n-1} + n\), for \(n \geq 2\). The general term of this sequence is

\[ T_n = 1 + 2 + \dots + n = \dfrac{1}{2}n(n+1). \]

These numbers may be represented graphically, as follows.

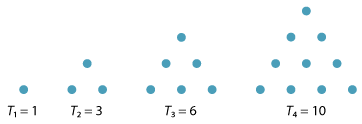
Detailed description
The first four triangular numbers.

The Greeks used geometric techniques to show that

\[ 1^2 + 2^2 + 3^2 + \dots + n^2 = \dfrac{1}{6}n(n+1)(2n+1) \] and \[ 1^3 + 2^3 + 3^3 + \dots + n^3 = \dfrac{1}{4}n^2(n+1)^2 = (1 + 2 + 3 + \dots + n)^2. \]

Next page - Answers to exercises